Bratteli Diagram on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, a Bratteli diagram is a combinatorial structure: a graph composed of vertices labelled by positive integers ("level") and unoriented edges between vertices having levels differing by one. The notion was introduced by
 An ordered Bratteli diagram is a Bratteli diagram together with a partial order on ''E''''n'' such that for any ''v'' ∈ ''V''''n'' the set is totally ordered. Edges that do not share a common range vertex are incomparable. This partial order allows us to define the set of all maximal edges ''E''max and the set of all minimal edges ''E''min. A Bratteli diagram with a unique infinitely long path in ''E''max and ''E''min is called ''essentially simple''.
An ordered Bratteli diagram is a Bratteli diagram together with a partial order on ''E''''n'' such that for any ''v'' ∈ ''V''''n'' the set is totally ordered. Edges that do not share a common range vertex are incomparable. This partial order allows us to define the set of all maximal edges ''E''max and the set of all minimal edges ''E''min. A Bratteli diagram with a unique infinitely long path in ''E''max and ''E''min is called ''essentially simple''.
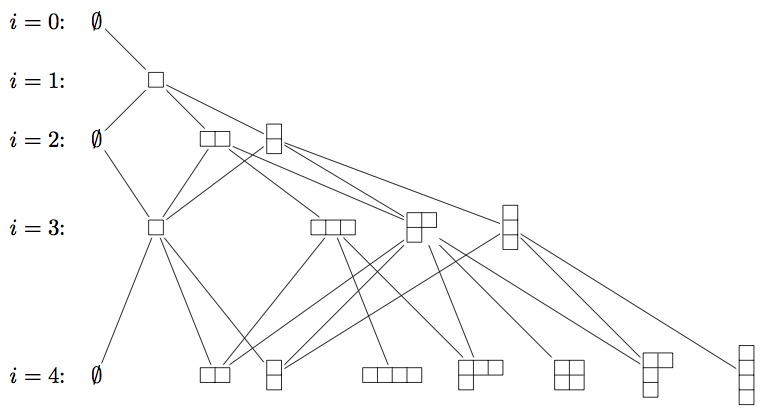 (1) If , the ith symmetric group, the corresponding Bratteli diagram is the same as Young's lattice.
(2) If is the
(1) If , the ith symmetric group, the corresponding Bratteli diagram is the same as Young's lattice.
(2) If is the
Ola Bratteli
Ola Bratteli (24 October 1946 – 8 February 2015) was a Norwegian mathematician.
He was a son of Trygve Bratteli and Randi Bratteli (née Larssen). He received a PhD degree in 1974. He was appointed as professor at the University of Trondhei ...
in 1972 in the theory of operator algebras to describe directed sequences of finite-dimensional algebras: it played an important role in Elliott's classification of AF-algebras and the theory of subfactor In the theory of von Neumann algebras, a subfactor of a factor M is a subalgebra that is a factor and contains 1 . The theory of subfactors led to the discovery of the
Jones polynomial in knot theory.
Index of a subfactor
Usually M is taken ...
s. Subsequently Anatoly Vershik
Anatoly Moiseevich Vershik (russian: Анато́лий Моисе́евич Ве́ршик; born on 28 December 1933 in Leningrad) is a Soviet and Russian mathematician. He is most famous for his joint work with Sergei V. Kerov on representatio ...
associated dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a ...
s with infinite paths in such graphs.
Definition
A Bratteli diagram is given by the following objects: * A sequence of sets ''V''''n'' ('the vertices at level ''n'' ') labeled by positive integer set N. In some literature each element v of ''V''''n'' is accompanied by a positive integer ''b''''v'' > 0. * A sequence of sets ''E''''n'' ('the edges from level ''n'' to ''n'' + 1 ') labeled by N, endowed with maps ''s'': ''E''''n'' → ''V''''n'' and ''r'': ''E''''n'' → ''V''''n''+1, such that: ** For each ''v'' in ''V''''n'', the number of elements ''e'' in ''E''''n'' with ''s''(''e'') = ''v'' is finite. ** So is the number of ''e'' ∈ ''E''''n''−1 with ''r''(''e'') = ''v''. ** When the vertices have markings by positive integers ''b''''v'', the number ''a''''v'', ''v'' ' of the edges with ''s''(''e'') = ''v'' and ''r''(''e'') = v' for ''v'' ∈ ''V''''n'' and v' ∈ ''V''''n''+1 satisfies ''b''''v'' ''a''v, v' ≤ ''b''v'. A customary way to pictorially represent Bratteli diagrams is to align the vertices according to their levels, and put the number ''b''''v'' beside the vertex ''v'', or use that number in place of ''v'', as inSequence of finite-dimensional algebras
Any semisimple algebra over the complex numbers C of finite dimension can be expressed as adirect sum
The direct sum is an operation between structures in abstract algebra, a branch of mathematics. It is defined differently, but analogously, for different kinds of structures. To see how the direct sum is used in abstract algebra, consider a more ...
⊕k Mnk(C) of matrix algebras, and the C-algebra homomorphisms between two such algebras up to inner automorphisms on both sides are completely determined by the multiplicity number between 'matrix algebra' components. Thus, an injective homomorphism of ⊕''k''=1''i'' ''M''''n''''k''(C) into ⊕''l''=1''j'' ''M''''m''''l''(C) may be represented by a collection of positive numbers ''a''''k'', ''l'' satisfying Σ ''n''''k'' ''a''''k'', l ≤ ''m''''l''. (The equality holds if and only if the homomorphism is unital; we can allow non-injective homomorphisms by allowing some ''a''''k'',''l'' to be zero.) This can be illustrated as a bipartite graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are ...
having the vertices marked by numbers (''n''''k'')''k'' on one hand and the ones marked by (''m''''l'')''l'' on the other hand, and having ''a''''k'', ''l'' edges between the vertex ''n''''k'' and the vertex ''m''''l''.
Thus, when we have a sequence of finite-dimensional semisimple algebras ''A''''n'' and injective homomorphisms ''φ''''n'' : ''A''''n → ''A''''n''+1: between them, we obtain a Bratteli diagram by putting
: ''V''''n'' = the set of simple components of ''A''''n''
(each isomorphic to a matrix algebra), marked by the size of matrices.
: (''E''''n'', ''r'', ''s''): the number of the edges between ''M''''n''''k''(C) ⊂ ''A''''n'' and ''M''''m''''l''(C) ⊂ ''A''''n''+1 is equal to the multiplicity of ''M''''n''''k''(C) into ''M''''m''''l''(C) under ''φ''''n''.
Sequence of split semisimple algebras
Any semisimple algebra (possibly of infinite dimension) is one whosemodules
Broadly speaking, modularity is the degree to which a system's components may be separated and recombined, often with the benefit of flexibility and variety in use. The concept of modularity is used primarily to reduce complexity by breaking a sy ...
are completely reducible, i.e. they decompose into the direct sum of simple modules. Let be a chain of split semisimple algebras, and let be the indexing set for the irreducible representations of . Denote by the irreducible module indexed by . Because of the inclusion , any -module restricts to a -module. Let denote the decomposition numbers
:
The Bratteli diagram for the chain is obtained by placing one vertex for every element of on level and connecting a vertex on level to a vertex on level with edges.
Examples
 (1) If , the ith symmetric group, the corresponding Bratteli diagram is the same as Young's lattice.
(2) If is the
(1) If , the ith symmetric group, the corresponding Bratteli diagram is the same as Young's lattice.
(2) If is the Brauer algebra In mathematics, a Brauer algebra is an associative algebra introduced by Richard Brauer in the context of the representation theory of the orthogonal group. It plays the same role that the symmetric group does for the representation theory of the ...
or the Birman–Wenzl algebra
In mathematics, the Birman–Murakami–Wenzl (BMW) algebra, introduced by and , is a two-parameter family of algebras \mathrm_n(\ell,m) of dimension 1\cdot 3\cdot 5\cdots (2n-1) having the Hecke algebra of the symmetric group as a quotient. It i ...
on ''i'' strands, then the resulting Bratteli diagram has partitions of ''i''–2''k'' (for ) with one edge between partitions on adjacent levels if one can be obtained from the other by adding or subtracting 1 from a single part.
(3) If is the Temperley–Lieb algebra In statistical mechanics, the Temperley–Lieb algebra is an algebra from which are built certain transfer matrices, invented by Neville Temperley and Elliott Lieb. It is also related to integrable models, knot theory and the braid group, quant ...
on ''i'' strands, the resulting Bratteli has integers ''i''–2''k'' (for ) with one edge between integers on adjacent levels if one can be obtained from the other by adding or subtracting 1.
See also
*Bratteli–Vershik diagram In mathematics, a Bratteli–Veršik diagram is an ordered, essentially simple Bratteli diagram (''V'', ''E'') with a homeomorphism on the set of all infinite paths called the Veršhik transformation. It is named after Ola Bratteli and Anatoly ...
References
* * * * {{refend Application-specific graphs Operator algebras