Bootstrap Aggregating on:
[Wikipedia]
[Google]
[Amazon]
Bootstrap aggregating, also called bagging (from bootstrap aggregating) or bootstrapping, is a
 Bagging leads to "improvements for unstable procedures", which include, for example,
Bagging leads to "improvements for unstable procedures", which include, for example,
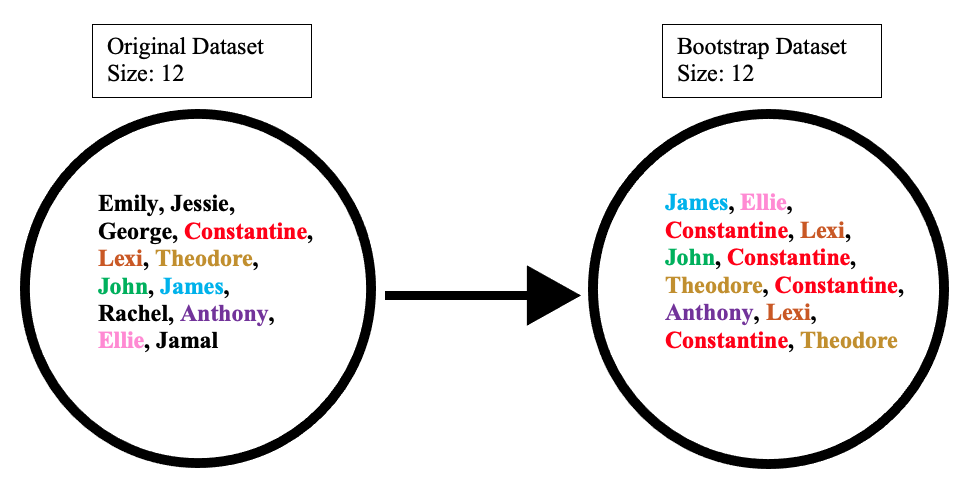 Suppose the original dataset is a group of 12 people. Their names are Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie, and Jamal.
By randomly picking a group of names, let us say our bootstrap dataset had James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine, and Theodore. In this case, the bootstrap sample contained four duplicates for Constantine, and two duplicates for Lexi, and Theodore.
Suppose the original dataset is a group of 12 people. Their names are Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie, and Jamal.
By randomly picking a group of names, let us say our bootstrap dataset had James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine, and Theodore. In this case, the bootstrap sample contained four duplicates for Constantine, and two duplicates for Lexi, and Theodore.

 This process is repeated recursively for successive levels of the tree until the desired depth is reached. At the very bottom of the tree, samples that test positive for the final feature are generally classified as positive, while those that lack the feature are classified as negative. These trees are then used as predictors to classify new data.
This process is repeated recursively for successive levels of the tree until the desired depth is reached. At the very bottom of the tree, samples that test positive for the final feature are generally classified as positive, while those that lack the feature are classified as negative. These trees are then used as predictors to classify new data.
 Because of their properties, random forests are considered one of the most accurate data mining algorithms, are less likely to
Because of their properties, random forests are considered one of the most accurate data mining algorithms, are less likely to
 For classification, use a training set , Inducer and the number of bootstrap samples as input. Generate a classifier as output
# Create new training sets , from with replacement
# Classifier is built from each set using to determine the classification of set
# Finally classifier is generated by using the previously created set of classifiers on the original dataset , the classification predicted most often by the sub-classifiers is the final classification
For classification, use a training set , Inducer and the number of bootstrap samples as input. Generate a classifier as output
# Create new training sets , from with replacement
# Classifier is built from each set using to determine the classification of set
# Finally classifier is generated by using the previously created set of classifiers on the original dataset , the classification predicted most often by the sub-classifiers is the final classification
machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
(ML) ensemble meta-algorithm designed to improve the stability
Stability may refer to:
Mathematics
*Stability theory, the study of the stability of solutions to differential equations and dynamical systems
** Asymptotic stability
** Exponential stability
** Linear stability
**Lyapunov stability
** Marginal s ...
and accuracy of ML classification
Classification is the activity of assigning objects to some pre-existing classes or categories. This is distinct from the task of establishing the classes themselves (for example through cluster analysis). Examples include diagnostic tests, identif ...
and regression algorithms. It also reduces variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
and overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
. Although it is usually applied to decision tree
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event ou ...
methods, it can be used with any type of method. Bagging is a special case of the ensemble averaging approach.
Description of the technique
Given a standardtraining set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from ...
of size , bagging generates new training sets , each of size , by sampling from uniformly and with replacement. By sampling with replacement, some observations may be repeated in each . If , then for large the set is expected to have the fraction (1 - 1/'' e'') (~63.2%) of the unique samples of , the rest being duplicates. This kind of sample is known as a bootstrap sample. Sampling with replacement ensures each bootstrap is independent from its peers, as it does not depend on previous chosen samples when sampling. Then, models are fitted using the above bootstrap samples and combined by averaging the output (for regression) or voting (for classification).
artificial neural networks
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
, classification and regression trees, and subset selection in linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
. Bagging was shown to improve preimage learning. On the other hand, it can mildly degrade the performance of stable methods such as ''k''-nearest neighbors.
Process of the algorithm
Key Terms
There are three types of datasets in bootstrap aggregating. These are the original, bootstrap, and out-of-bag datasets. Each section below will explain how each dataset is made except for the original dataset. The original dataset is whatever information is given.Creating the bootstrap dataset
The bootstrap dataset is made by randomly picking objects from the original dataset. Also, it must be the same size as the original dataset. However, the difference is that the bootstrap dataset can have duplicate objects. Here is a simple example to demonstrate how it works along with the illustration below: Suppose the original dataset is a group of 12 people. Their names are Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie, and Jamal.
By randomly picking a group of names, let us say our bootstrap dataset had James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine, and Theodore. In this case, the bootstrap sample contained four duplicates for Constantine, and two duplicates for Lexi, and Theodore.
Suppose the original dataset is a group of 12 people. Their names are Emily, Jessie, George, Constantine, Lexi, Theodore, John, James, Rachel, Anthony, Ellie, and Jamal.
By randomly picking a group of names, let us say our bootstrap dataset had James, Ellie, Constantine, Lexi, John, Constantine, Theodore, Constantine, Anthony, Lexi, Constantine, and Theodore. In this case, the bootstrap sample contained four duplicates for Constantine, and two duplicates for Lexi, and Theodore.
Creating the out-of-bag dataset
The out-of-bag dataset represents the remaining people who were not in the bootstrap dataset. It can be calculated by taking the difference between the original and the bootstrap datasets. In this case, the remaining samples who were not selected are Emily, Jessie, George, Rachel, and Jamal. Keep in mind that since both datasets are sets, when taking the difference the duplicate names are ignored in the bootstrap dataset. The illustration below shows how the math is done:
Application
Creating the bootstrap and out-of-bag datasets is crucial since it is used to test the accuracy ofensemble learning
In statistics and machine learning, ensemble methods use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone.
Unlike a statistical ensemble in statist ...
algorithms like random forest
Random forests or random decision forests is an ensemble learning method for statistical classification, classification, regression analysis, regression and other tasks that works by creating a multitude of decision tree learning, decision trees ...
. For example, a model that produces 50 trees using the bootstrap/out-of-bag datasets will have a better accuracy than if it produced 10 trees. Since the algorithm generates multiple trees and therefore multiple datasets the chance that an object is left out of the bootstrap dataset is low. The next few sections talk about how the random forest algorithm works in more detail.
Creation of Decision Trees
The next step of the algorithm involves the generation ofdecision tree
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event ou ...
s from the bootstrapped dataset. To achieve this, the process examines each gene/feature and determines for how many samples the feature's presence or absence yields a positive or negative result. This information is then used to compute a confusion matrix
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as error matrix, is a specific table layout that allows visualization of the performance of an algorithm, typically a super ...
, which lists the true positives, false positives, true negatives, and false negatives of the feature when used as a classifier. These features are then ranked according to various classification metrics based on their confusion matrices. Some common metrics include estimate of positive correctness (calculated by subtracting false positives from true positives), measure of "goodness", and information gain
Information is an abstract concept that refers to something which has the power to inform. At the most fundamental level, it pertains to the interpretation (perhaps formally) of that which may be sensed, or their abstractions. Any natur ...
. These features are then used to partition the samples into two sets: those that possess the top feature, and those that do not.
The diagram below shows a decision tree of depth two being used to classify data. For example, a data point that exhibits Feature 1, but not Feature 2, will be given a "No". Another point that does not exhibit Feature 1, but does exhibit Feature 3, will be given a "Yes".
 This process is repeated recursively for successive levels of the tree until the desired depth is reached. At the very bottom of the tree, samples that test positive for the final feature are generally classified as positive, while those that lack the feature are classified as negative. These trees are then used as predictors to classify new data.
This process is repeated recursively for successive levels of the tree until the desired depth is reached. At the very bottom of the tree, samples that test positive for the final feature are generally classified as positive, while those that lack the feature are classified as negative. These trees are then used as predictors to classify new data.
Random Forests
The next part of the algorithm involves introducing yet another element of variability amongst the bootstrapped trees. In addition to each tree only examining a bootstrapped set of samples, only a small but consistent number of unique features are considered when ranking them as classifiers. This means that each tree only knows about the data pertaining to a small constant number of features, and a variable number of samples that is less than or equal to that of the original dataset. Consequently, the trees are more likely to return a wider array of answers, derived from more diverse knowledge. This results in arandom forest
Random forests or random decision forests is an ensemble learning method for statistical classification, classification, regression analysis, regression and other tasks that works by creating a multitude of decision tree learning, decision trees ...
, which possesses numerous benefits over a single decision tree generated without randomness. In a random forest, each tree "votes" on whether or not to classify a sample as positive based on its features. The sample is then classified based on majority vote. An example of this is given in the diagram below, where the four trees in a random forest vote on whether or not a patient with mutations A, B, F, and G has cancer. Since three out of four trees vote yes, the patient is then classified as cancer positive.
 Because of their properties, random forests are considered one of the most accurate data mining algorithms, are less likely to
Because of their properties, random forests are considered one of the most accurate data mining algorithms, are less likely to overfit
mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfitt ...
their data, and run quickly and efficiently even for large datasets. They are primarily useful for classification as opposed to regression, which attempts to draw observed connections between statistical variables in a dataset. This makes random forests particularly useful in such fields as banking, healthcare, the stock market, and e-commerce
E-commerce (electronic commerce) refers to commercial activities including the electronic buying or selling products and services which are conducted on online platforms or over the Internet. E-commerce draws on technologies such as mobile co ...
where it is important to be able to predict future results based on past data. One of their applications would be as a useful tool for predicting cancer based on genetic factors, as seen in the above example.
There are several important factors to consider when designing a random forest. If the trees in the random forests are too deep, overfitting can still occur due to over-specificity. If the forest is too large, the algorithm may become less efficient due to an increased runtime. Random forests also do not generally perform well when given sparse data with little variability. However, they still have numerous advantages over similar data classification algorithms such as neural network
A neural network is a group of interconnected units called neurons that send signals to one another. Neurons can be either biological cells or signal pathways. While individual neurons are simple, many of them together in a network can perfor ...
s, as they are much easier to interpret and generally require less data for training. As an integral component of random forests, bootstrap aggregating is very important to classification algorithms, and provides a critical element of variability that allows for increased accuracy when analyzing new data, as discussed below.
Improving Random Forests and Bagging
While the techniques described above utilizerandom forest
Random forests or random decision forests is an ensemble learning method for statistical classification, classification, regression analysis, regression and other tasks that works by creating a multitude of decision tree learning, decision trees ...
s and bagging (otherwise known as bootstrapping), there are certain techniques that can be used in order to improve their execution and voting time, their prediction accuracy, and their overall performance. The following are key steps in creating an efficient random forest:
# Specify the maximum depth of trees: Instead of allowing the random forest to continue until all nodes are pure, it is better to cut it off at a certain point in order to further decrease chances of overfitting.
# Prune the dataset: Using an extremely large dataset may create results that are less indicative of the data provided than a smaller set that more accurately represents what is being focused on.
#* Continue pruning the data at each node split rather than just in the original bagging process.
# Decide on accuracy or speed: Depending on the desired results, increasing or decreasing the number of trees within the forest can help. Increasing the number of trees generally provides more accurate results while decreasing the number of trees will provide quicker results.
Algorithm (classification)
 For classification, use a training set , Inducer and the number of bootstrap samples as input. Generate a classifier as output
# Create new training sets , from with replacement
# Classifier is built from each set using to determine the classification of set
# Finally classifier is generated by using the previously created set of classifiers on the original dataset , the classification predicted most often by the sub-classifiers is the final classification
For classification, use a training set , Inducer and the number of bootstrap samples as input. Generate a classifier as output
# Create new training sets , from with replacement
# Classifier is built from each set using to determine the classification of set
# Finally classifier is generated by using the previously created set of classifiers on the original dataset , the classification predicted most often by the sub-classifiers is the final classification
for i = 1 to m
C*(x) = argmax # (most often predicted label y)
y∈Y
Example: ozone data
To illustrate the basic principles of bagging, below is an analysis on the relationship betweenozone
Ozone () (or trioxygen) is an Inorganic compound, inorganic molecule with the chemical formula . It is a pale blue gas with a distinctively pungent smell. It is an allotrope of oxygen that is much less stable than the diatomic allotrope , break ...
and temperature (data from Rousseeuw and Leroy (1986), analysis done in R).
The relationship between temperature and ozone appears to be nonlinear in this dataset, based on the scatter plot. To mathematically describe this relationship, LOESS
A loess (, ; from ) is a clastic rock, clastic, predominantly silt-sized sediment that is formed by the accumulation of wind-blown dust. Ten percent of Earth's land area is covered by loesses or similar deposition (geology), deposits.
A loess ...
smoothers (with bandwidth 0.5) are used. Rather than building a single smoother for the complete dataset, 100 bootstrap samples were drawn. Each sample is composed of a random subset of the original data and maintains a semblance of the master set's distribution and variability. For each bootstrap sample, a LOESS smoother was fit. Predictions from these 100 smoothers were then made across the range of the data. The black lines represent these initial predictions. The lines lack agreement in their predictions and tend to overfit their data points: evident by the wobbly flow of the lines.
center
By taking the average of 100 smoothers, each corresponding to a subset of the original dataset, we arrive at one bagged predictor (red line). The red line's flow is stable and does not overly conform to any data point(s).
Advantages and disadvantages
Advantages: * Many weak learners aggregated typically outperform a single learner over the entire set, and have less overfit * Reduces variance in high-variance low-bias weak learner, which can improveefficiency (statistics)
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achiev ...
* Can be performed in parallel, as each separate bootstrap can be processed on its own before aggregation.
Disadvantages:
* For a weak learner with high bias, bagging will also carry high bias into its aggregate
* Loss of interpretability of a model.
* Can be computationally expensive depending on the dataset.
History
The concept of bootstrap aggregating is derived from the concept of bootstrapping which was developed by Bradley Efron. Bootstrap aggregating was proposed by Leo Breiman who also coined the abbreviated term "bagging" (bootstrap aggregating). Breiman developed the concept of bagging in 1994 to improve classification by combining classifications of randomly generated training sets. He argued, "If perturbing the learning set can cause significant changes in the predictor constructed, then bagging can improve accuracy".See also
*Boosting (machine learning)
In machine learning (ML), boosting is an Ensemble learning, ensemble metaheuristic for primarily reducing Bias–variance tradeoff, bias (as opposed to variance). It can also improve the Stability (learning theory), stability and accuracy of ML S ...
*Bootstrapping (statistics)
Bootstrapping is a procedure for estimating the distribution of an estimator by resampling (often with replacement) one's data or a model estimated from the data. Bootstrapping assigns measures of accuracy ( bias, variance, confidence interval ...
*Cross-validation (statistics)
Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistics, statistical analysis will Generalization error, generalize to ...
* Out-of-bag error
*Random forest
Random forests or random decision forests is an ensemble learning method for statistical classification, classification, regression analysis, regression and other tasks that works by creating a multitude of decision tree learning, decision trees ...
* Random subspace method (attribute bagging)
* Resampled efficient frontier
* Predictive analysis: Classification and regression trees
References
Further reading
* * * * {{cite book , first1=Bradley , last1=Boehmke , first2=Brandon , last2=Greenwell , chapter=Bagging , pages=191–202 , title=Hands-On Machine Learning with R , publisher=Chapman & Hall , year=2019 , isbn=978-1-138-49568-5 Ensemble learning Machine learning algorithms Computational statistics