Block Sort on:
[Wikipedia]
[Google]
[Amazon]
//_else_the_ranges_are_already_correctly_ordered
Fixed-point_arithmetic.html" ;"title="id_−_1>_array[mid.html" ;"title="id_−_1.html" ;"title="tart, end))
else if (array[mid − 1">tart, end))
else if (array[mid − 1> array[mid">id_−_1.html" ;"title="tart, end))
else if (array[mid − 1">tart, end))
else if (array[mid − 1> array[mid
Merge(array, A = [start, mid), B = [mid, end))
// else the ranges are already correctly ordered
Fixed-point arithmetic">Fixed-point math may also be used, by representing the scale factor as a fraction
The two internal buffers needed for each level of the merge step are created by moving the first 2 first instances of their values within an subarray to the start of . First it iterates over the elements in and counts off the unique values it needs, then it applies array rotations to move those unique values to the start. If A did not contain enough unique values to fill the two buffers (of size each), can be used just as well. In this case it moves the ''last'' instance of each value to the ''end'' of , with that part of not being included during the merges.
while (integer_step < array.size)
block_size =
buffer_size = integer_step/block_size + 1
xtract two buffers of size 'buffer_size' each/span>
If does not contain enough unique values either, it pulls out the largest number of unique values it ''could'' find, then adjusts the size of the and blocks such that the number of resulting blocks is less than or equal to the number of unique items pulled out for the buffer. Only one buffer will be used in this case – the second buffer won't exist.
buffer_size = umber of unique values found/span>
block_size = integer_step/buffer_size + 1
integer_part = numerator = 0
while (integer_part < array.size)
et the ranges for A and B/span>
djust A and B to not include the ranges used by the buffers/span>
Once the one or two internal buffers have been created, it begins merging each and subarray for this level of the merge sort. To do so, it divides each A and B subarray into evenly sized blocks of the size calculated in the previous step, where the first block and last block are unevenly sized if needed. It then loops over each of the evenly sized A blocks and swaps the second value with a corresponding value from the first of the two internal buffers. This is known as ''tagging'' the blocks.
// blockA is the range of the remaining A blocks,
// and firstA is the unevenly sized first A block
blockA = [A.start, A.end)
firstA = [A.start, A.start + , blockA, % block_size)
// swap the second value of each A block with the value in buffer1
for (index = 0, indexA = firstA.end + 1; indexA < blockA.end; indexA += block_size)
Swap(array[buffer1.start + index], array[indexA])
index++
lastA = firstA
blockB = [B.start, B.start + minimum(block_size, , B, ))
blockA.start += , firstA,
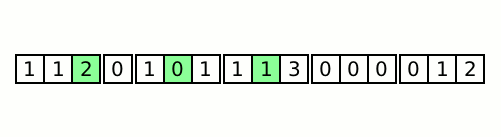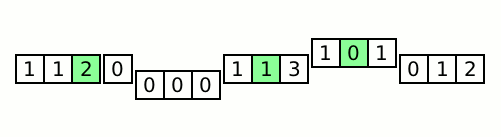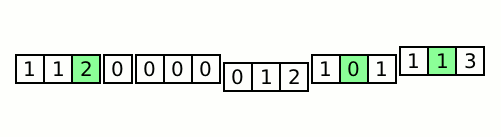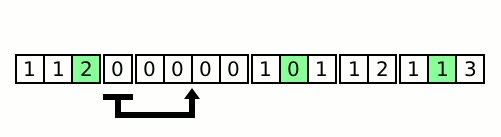After defining and tagging the A blocks in this manner, the A blocks are ''rolled'' through the B blocks by block swapping the first evenly sized A block with the next B block. This process repeats until the first value of the A block with the smallest tag value is less than or equal to the last value of the B block that was just swapped with an A block.
At that point, the minimum A block (the A block with the smallest tag value) is swapped to the start of the rolling A blocks and the tagged value is restored with its original value from the first buffer. This is known as ''dropping'' a block behind, as it will no longer be rolled along with the remaining A blocks. That A block is then inserted into the previous B block, first by using a binary search on B to find the index where the first value of A is less than or equal to the value at that index of B, and then by rotating A into B at that index.
minA = blockA.start
indexA = 0
while (true)
// if there's a previous B block and the first value of the minimum A block is ≤
// the last value of the previous B block, then drop that minimum A block behind.
// or if there are no B blocks left then keep dropping the remaining A blocks.
if ((, lastB, > 0 and array astB.end - 1≥ array inA or , blockB, = 0)
// figure out where to split the previous B block, and rotate it at the split
B_split = BinaryFirst(array, array inA lastB)
B_remaining = lastB.end - B_split
// swap the minimum A block to the beginning of the rolling A blocks
BlockSwap(array, blockA.start, minA, block_size)
// restore the second value for the A block
Swap(array lockA.start + 1 array uffer1.start + indexA
indexA++
// rotate the A block into the previous B block
Rotate(array, blockA.start - B_split, [B_split, blockA.start + block_size))
// locally merge the previous A block with the B values that follow it,
// using the second internal buffer as swap space (if it exists)
if (, buffer2, > 0)
MergeInternal(array, lastA, [lastA.end, B_split), buffer2)
else
MergeInPlace(array, lastA, [lastA.end, B_split))
// update the range for the remaining A blocks,
// and the range remaining from the B block after it was split
lastA = [blockA.start - B_remaining, blockA.start - B_remaining + block_size)
lastB = [lastA.end, lastA.end + B_remaining)
// if there are no more A blocks remaining, this step is finished
blockA.start = blockA.start + block_size
if (, blockA, = 0)
break
minA = [new minimum A block] ''(see below)''
else if (, blockB, < block_size)
// move the last B block, which is unevenly sized,
// to before the remaining A blocks, by using a rotation
Rotate(array, blockB.start - blockA.start, [blockA.start, blockB.end))
lastB = [blockA.start, blockA.start + , blockB, )
blockA.start += , blockB,
blockA.end += , blockB,
minA += , blockB,
blockB.end = blockB.start
else
// roll the leftmost A block to the end by swapping it with the next B block
BlockSwap(array, blockA.start, blockB.start, block_size)
lastB = [blockA.start, blockA.start + block_size)
if (minA = blockA.start)
minA = blockA.end
blockA.start += block_size
blockA.end += block_size
blockB.start += block_size
// this is equivalent to minimum(blockB.end + block_size, B.end),
// but that has the potential to Integer overflow, overflow
if (blockB.end > B.end - block_size)
blockB.end = B.end
else
blockB.end += block_size
// merge the last A block with the remaining B values
if (, buffer2, > 0)
MergeInternal(array, lastA, _When_the_minimum_A_block_is_dropped_behind_and_needs_to_be_rotated_into_the_previous_B_block,_after_which_its_contents_are_swapped_into_the_second_internal_buffer_for_the_local_merges,_it_would_be_faster_to_swap_the_A_block_to_the_buffer_beforehand,_and_to_take_advantage_of_the_fact_that_the_contents_of_that_buffer_do_not_need_to_retain_any_order._So_rather_than_rotating_the_second_buffer_(which_used_to_be_the_A_block_before_the_block_swap)_into_the_previous_B_block_at_position_''index'',_the_values_in_the_B_block_after_''index''_can_simply_be_block_swapped_with_the_last_items_of_the_buffer.
The_''floating_hole''_in_this_case_refers_to_the_contents_of_the_second_internal_buffer_''floating''_around_the_array,_and_acting_as_a_''hole''_in_the_sense_that_the_items_do_not_need_to_retain_their_order.
//_block_swap_the_values_in_A_with_those_in_'buffer'
________BlockSwap(array,_A.start,_buffer.start,_.html" ;"title="astA.end, B.end), buffer2)
else
MergeInPlace(array, lastA, [lastA.end, B.end))
One optimization that can be applied during this step is the ''floating-hole technique''. When the minimum A block is dropped behind and needs to be rotated into the previous B block, after which its contents are swapped into the second internal buffer for the local merges, it would be faster to swap the A block to the buffer beforehand, and to take advantage of the fact that the contents of that buffer do not need to retain any order. So rather than rotating the second buffer (which used to be the A block before the block swap) into the previous B block at position ''index'', the values in the B block after ''index'' can simply be block swapped with the last items of the buffer.
The ''floating hole'' in this case refers to the contents of the second internal buffer ''floating'' around the array, and acting as a ''hole'' in the sense that the items do not need to retain their order.
Block sort, or block merge sort, is a
_FloorPowerOfTwo(x)
_____x_=_x_.html" ;"title="Floor_and_ceiling_functions.html" "title="ange.start, range.start + amount))
Reverse(array, [range.start + amount, range.end))
* Floor power of two: Floor and ceiling functions">floor
A floor is the bottom surface of a room or vehicle. Floors vary from simple dirt in a cave to many layered surfaces made with modern technology. Floors may be stone, wood, bamboo, metal or any other material that can support the expected load ...
a value to the next power of two. Thus 63 becomes 32, 64 stays 64, and so forth.
FloorPowerOfTwo(x)
x = x "> (x >> 1)
x = x , (x >> 2)
x = x , (x >> 4)
x = x , (x >> 8)
x = x , (x >> 16)
if (this is a 64-bit computing, 64-bit system)
x = x , (x >> 32)
return x - (x >> 1)
sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a List (computing), list into an Total order, order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. ...
combining at least two merge
Merge, merging, or merger may refer to:
Concepts
* Merge (traffic), the reduction of the number of lanes on a road
* Merge (linguistics), a basic syntactic operation in generative syntax in the Minimalist Program
* Merger (politics), the comb ...
operations with an insertion sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. Howev ...
to arrive at in-place
In computer science, an in-place algorithm is an algorithm which transforms input using no auxiliary data structure. However, a small amount of extra storage space is allowed for auxiliary variables. The input is usually overwritten by the output ...
stable
A stable is a building in which livestock, especially horses, are kept. It most commonly means a building that is divided into separate stalls for individual animals and livestock. There are many different types of stables in use today; the ...
sorting. It gets its name from the observation that merging two sorted lists, and , is equivalent to breaking into evenly sized ''blocks'', inserting each block into under special rules, and merging pairs.
One practical algorithm for O(log n) in place merging was proposed by Pok-Son Kim and Arne Kutzner in 2008.
Overview
The outer loop of block sort is identical to a bottom-up merge sort, where each ''level'' of the sort merges pairs of subarrays, and , in sizes of 1, then 2, then 4, 8, 16, and so on, until both subarrays combined are the array itself. Rather than merging and directly as with traditional methods, a block-based merge algorithm divides into discrete blocks of size (resulting in ''number'' of blocks as well), inserts each block into such that the first value of each block is less than or equal (≤) to the value immediately after it, then ''locally merges'' each block with any values between it and the next block. As merges still require a separate buffer large enough to hold the block to be merged, two areas within the array are reserved for this purpose (known as ''internal buffers''). The first two blocks are thus modified to contain the first instance of each value within , with the original contents of those blocks shifted over if necessary. The remaining blocks are then inserted into and merged using one of the two buffers as swap space. This process causes the values in that buffer to be rearranged. Once every and block of every and subarray have been merged for that level of the merge sort, the values in that buffer must be sorted to restore their original order, so an insertion sort must be applied. The values in the buffers are then redistributed to their first sorted position within the array. This process repeats for each level of the outer bottom-up merge sort, at which point the array will have been stably sorted.Algorithm
The following operators are used in the code examples: Additionally, block sort relies on the following operations as part of its overall algorithm: *Swap
Swap or SWAP may refer to:
Finance
* Swap (finance), a derivative in which two parties agree to exchange one stream of cash flows against another
* Barter
Science and technology
* Swap (computer programming), exchanging two variables in t ...
: exchange the positions of two values in an array.
* Block swap: exchange a range of values within an array with values in a different range of the array.
* Binary search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the m ...
: assuming the array is sorted, check the middle value of the current search range, then if the value is lesser check the lower range, and if the value is greater check the upper range. Block sort uses two variants: one which finds the ''first'' position to insert a value in the sorted array, and one which finds the ''last'' position.
* Linear search
In computer science, a linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched.
A linear search runs in at ...
: find a particular value in an array by checking every single element in order, until it is found.
* Insertion sort
Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. Howev ...
: for each item in the array, loop backward and find where it needs to be inserted, then insert it at that position.
* Array rotation: move the items in an array to the left or right by some number of spaces, with values on the edges wrapping around to the other side. Rotations can be implemented as three reversals.
Rotate(array, amount, range)
Reverse(array, range)
Reverse(array, floor_
A_floor_is_the_bottom_surface_of_a_room_or_vehicle._Floors_vary_from__simple_dirt_in_a_cave_to_many_layered_surfaces_made_with_modern_technology._Floors_may_be_stone,_wood,_bamboo,_metal_or_any_other_material_that_can_support_the_expected_load_...
_a_value_to_the_next_power_of_two._Thus_63_becomes_32,_64_stays_64,_and_so_forth.Outer loop
As previously stated, the outer loop of a block sort is identical to a bottom-up merge sort. However, it benefits from the variant that ensures each and subarray are the same size to within one item: BlockSort(array) power_of_two = FloorPowerOfTwo(array.size) scale = array.size/power_of_two // 1.0 ≤ scale < 2.0 // insertion sort 16–31 items at a time for (merge = 0; merge < power_of_two; merge += 16) start = merge * scale end = start + 16 * scale InsertionSort(array, [start, end)) for (length = 16; length < power_of_two; length += length) for (merge = 0; merge < power_of_two; merge += length * 2) start = merge * scale mid = (merge + length) * scale end = (merge + length * 2) * scale if (array[end − 1] < array[start]) // the two ranges are in reverse order, so a rotation is enough to merge them Rotate(array, mid − start, tart,_end)) ________________else_if_(array tart,_end)) ________________else_if_(array[mid_−_1>_array[mid">id_−_1.html"_;"title="tart,_end)) ________________else_if_(array[mid_−_1">tart,_end)) ________________else_if_(array[mid_−_1>_array[mid ____________________Merge(array,_A_=_[start,_mid),_B_=_[mid,_end)) ________________integer_part + numerator/denominator:
power_of_two = FloorPowerOfTwo(array.size)
denominator = power_of_two/16
numerator_step = array.size % denominator
integer_step = floor(array.size/denominator)
// insertion sort 16–31 items at a time
while (integer_step < array.size)
integer_part = numerator = 0
while (integer_part < array.size)
// get the ranges for A and B
start = integer_part
integer_part += integer_step
numerator += numerator_step
if (numerator ≥ denominator)
numerator −= denominator
integer_part++
mid = integer_part
integer_part += integer_step
numerator += numerator_step
if (numerator ≥ denominator)
numerator −= denominator
integer_part++
end = integer_part
if (array[end − 1] < array[start])
Rotate(array, mid − start, [start, end))
else if (array[mid − 1] > array[mid])
Merge(array, A = [start, mid), B = [mid, end))
integer_step += integer_step
numerator_step += numerator_step
if (numerator_step ≥ denominator)
numerator_step −= denominator
integer_step++
Extract buffers
The two internal buffers needed for each level of the merge step are created by moving the first 2 first instances of their values within an subarray to the start of . First it iterates over the elements in and counts off the unique values it needs, then it applies array rotations to move those unique values to the start. If A did not contain enough unique values to fill the two buffers (of size each), can be used just as well. In this case it moves the ''last'' instance of each value to the ''end'' of , with that part of not being included during the merges.
while (integer_step < array.size)
block_size =
buffer_size = integer_step/block_size + 1
xtract two buffers of size 'buffer_size' each/span>
If does not contain enough unique values either, it pulls out the largest number of unique values it ''could'' find, then adjusts the size of the and blocks such that the number of resulting blocks is less than or equal to the number of unique items pulled out for the buffer. Only one buffer will be used in this case – the second buffer won't exist.
buffer_size = umber of unique values found/span>
block_size = integer_step/buffer_size + 1
integer_part = numerator = 0
while (integer_part < array.size)
et the ranges for A and B/span>
djust A and B to not include the ranges used by the buffers/span>
Tag A blocks
Once the one or two internal buffers have been created, it begins merging each and subarray for this level of the merge sort. To do so, it divides each A and B subarray into evenly sized blocks of the size calculated in the previous step, where the first block and last block are unevenly sized if needed. It then loops over each of the evenly sized A blocks and swaps the second value with a corresponding value from the first of the two internal buffers. This is known as ''tagging'' the blocks.
// blockA is the range of the remaining A blocks,
// and firstA is the unevenly sized first A block
blockA = [A.start, A.end)
firstA = [A.start, A.start + , blockA, % block_size)
// swap the second value of each A block with the value in buffer1
for (index = 0, indexA = firstA.end + 1; indexA < blockA.end; indexA += block_size)
Swap(array[buffer1.start + index], array[indexA])
index++
lastA = firstA
blockB = [B.start, B.start + minimum(block_size, , B, ))
blockA.start += , firstA,
Roll and drop
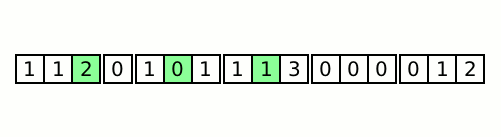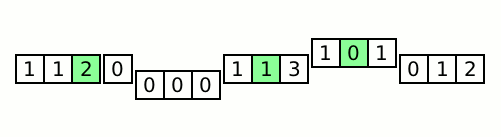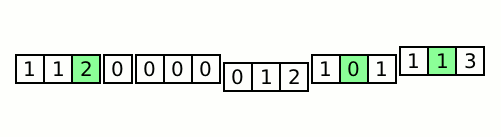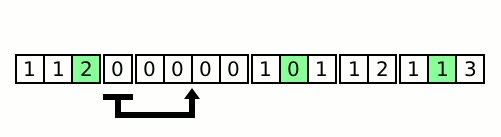After defining and tagging the A blocks in this manner, the A blocks are ''rolled'' through the B blocks by block swapping the first evenly sized A block with the next B block. This process repeats until the first value of the A block with the smallest tag value is less than or equal to the last value of the B block that was just swapped with an A block.
At that point, the minimum A block (the A block with the smallest tag value) is swapped to the start of the rolling A blocks and the tagged value is restored with its original value from the first buffer. This is known as ''dropping'' a block behind, as it will no longer be rolled along with the remaining A blocks. That A block is then inserted into the previous B block, first by using a binary search on B to find the index where the first value of A is less than or equal to the value at that index of B, and then by rotating A into B at that index.
minA = blockA.start
indexA = 0
while (true)
// if there's a previous B block and the first value of the minimum A block is ≤
// the last value of the previous B block, then drop that minimum A block behind.
// or if there are no B blocks left then keep dropping the remaining A blocks.
if ((, lastB, > 0 and array astB.end - 1≥ array inA or , blockB, = 0)
// figure out where to split the previous B block, and rotate it at the split
B_split = BinaryFirst(array, array inA lastB)
B_remaining = lastB.end - B_split
// swap the minimum A block to the beginning of the rolling A blocks
BlockSwap(array, blockA.start, minA, block_size)
// restore the second value for the A block
Swap(array lockA.start + 1 array uffer1.start + indexA
indexA++
// rotate the A block into the previous B block
Rotate(array, blockA.start - B_split, [B_split, blockA.start + block_size))
// locally merge the previous A block with the B values that follow it,
// using the second internal buffer as swap space (if it exists)
if (, buffer2, > 0)
MergeInternal(array, lastA, [lastA.end, B_split), buffer2)
else
MergeInPlace(array, lastA, [lastA.end, B_split))
// update the range for the remaining A blocks,
// and the range remaining from the B block after it was split
lastA = [blockA.start - B_remaining, blockA.start - B_remaining + block_size)
lastB = [lastA.end, lastA.end + B_remaining)
// if there are no more A blocks remaining, this step is finished
blockA.start = blockA.start + block_size
if (, blockA, = 0)
break
minA = [new minimum A block] ''(see below)''
else if (, blockB, < block_size)
// move the last B block, which is unevenly sized,
// to before the remaining A blocks, by using a rotation
Rotate(array, blockB.start - blockA.start, [blockA.start, blockB.end))
lastB = [blockA.start, blockA.start + , blockB, )
blockA.start += , blockB,
blockA.end += , blockB,
minA += , blockB,
blockB.end = blockB.start
else
// roll the leftmost A block to the end by swapping it with the next B block
BlockSwap(array, blockA.start, blockB.start, block_size)
lastB = [blockA.start, blockA.start + block_size)
if (minA = blockA.start)
minA = blockA.end
blockA.start += block_size
blockA.end += block_size
blockB.start += block_size
// this is equivalent to minimum(blockB.end + block_size, B.end),
// but that has the potential to Integer overflow, overflow
if (blockB.end > B.end - block_size)
blockB.end = B.end
else
blockB.end += block_size
// merge the last A block with the remaining B values
if (, buffer2, > 0)
MergeInternal(array, lastA, _When_the_minimum_A_block_is_dropped_behind_and_needs_to_be_rotated_into_the_previous_B_block,_after_which_its_contents_are_swapped_into_the_second_internal_buffer_for_the_local_merges,_it_would_be_faster_to_swap_the_A_block_to_the_buffer_beforehand,_and_to_take_advantage_of_the_fact_that_the_contents_of_that_buffer_do_not_need_to_retain_any_order._So_rather_than_rotating_the_second_buffer_(which_used_to_be_the_A_block_before_the_block_swap)_into_the_previous_B_block_at_position_''index'',_the_values_in_the_B_block_after_''index''_can_simply_be_block_swapped_with_the_last_items_of_the_buffer.
The_''floating_hole''_in_this_case_refers_to_the_contents_of_the_second_internal_buffer_''floating''_around_the_array,_and_acting_as_a_''hole''_in_the_sense_that_the_items_do_not_need_to_retain_their_order.
__Local_merges_
Once_the_A_block_has_been_rotated_into_the_B_block,_the_previous_A_block_is_then_merged_with_the_B_values_that_follow_it,_using_the_second_buffer_as_swap_space._When_the_first_A_block_is_dropped_behind_this_refers_to_the_unevenly_sized_A_block_at_the_start,_when_the_second_A_block_is_dropped_behind_it_means_the_first_A_block,_and_so_forth. ____MergeInternal(array,_A,_B,_buffer) ________Local merges
Once the A block has been rotated into the B block, the previous A block is then merged with the B values that follow it, using the second buffer as swap space. When the first A block is dropped behind this refers to the unevenly sized A block at the start, when the second A block is dropped behind it means the first A block, and so forth. MergeInternal(array, A, B, buffer) // block swap the values in A with those in 'buffer' BlockSwap(array, A.start, buffer.start, ">A, ) A_count = 0, B_count = 0, insert = 0 while (A_count < , A, and B_count < , B, ) if (array uffer.start_+_A_count≤_array[B.start_+_B_count ________________Swap(array[A.start_+_insert.html" ;"title=".start_+_B_count.html" ;"title="uffer.start + A_count≤ array[B.start + B_count">uffer.start + A_count≤ array[B.start + B_count Swap(array[A.start + insert">.start_+_B_count.html" ;"title="uffer.start + A_count≤ array[B.start + B_count">uffer.start + A_count≤ array[B.start + B_count Swap(array[A.start + insert array[buffer.start + A_count]) A_count++ else Swap(array[A.start + insert], array[B.start + B_count]) B_count++ insert++ // block swap the remaining part of the buffer with the remaining part of the array BlockSwap(array, buffer.start + A_count, A.start + insert, , A, - A_count) If the second buffer does not exist, a strictly in-place merge operation must be performed, such as a rotation-based version of the Hwang and Lin algorithm, the Dudzinski and Dydek algorithm, or a repeated binary search and rotate. MergeInPlace(array, A, B) while (, A, > 0 and , B, > 0) // find the first place in B where the first item in A needs to be inserted mid = BinaryFirst(array, array .start B) // rotate A into place amount = mid - A.end Rotate(array, amount, [A.start, mid)) // calculate the new A and B ranges B = [mid, B.end) A = [A.start + amount, mid) A.start = BinaryLast(array, array .start A) After dropping the minimum A block and merging the previous A block with the B values that follow it, the new minimum A block must be found within the blocks that are still being rolled through the array. This is handled by running a linear search through those A blocks and comparing the tag values to find the smallest one. minA = blockA.start for (findA = minA + block_size; findA < blockA.end - 1; findA += block_size) if (array[findA + 1] < array[minA + 1]) minA = findA These remaining A blocks then continue rolling through the array and being dropped and inserted where they belong. This process repeats until all of the A blocks have been dropped and rotated into the previous B block. Once the last remaining A block has been dropped behind and inserted into B where it belongs, it should be merged with the remaining B values that follow it. This completes the merge process for that particular pair of A and B subarrays. However, it must then repeat the process for the remaining A and B subarrays for the current level of the merge sort. Note that the internal buffers can be reused for every set of A and B subarrays for this level of the merge sort, and do not need to be re-extracted or modified in any way.Redistribute
After all of the A and B subarrays have been merged, the one or two internal buffers are still left over. The first internal buffer was used for tagging the A blocks, and its contents are still in the same order as before, but the second internal buffer may have had its contents rearranged when it was used as swap space for the merges. This means the contents of the second buffer will need to be sorted using a different algorithm, such as insertion sort. The two buffers must then be redistributed back into the array using the opposite process that was used to create them. After repeating these steps for every level of the bottom-up merge sort, the block sort is completed.Variants
Block sort works by extracting two internal buffers, breaking A and B subarrays into evenly sized blocks, rolling and dropping the A blocks into B (using the first buffer to track the order of the A blocks), locally merging using the second buffer as swap space, sorting the second buffer, and redistributing both buffers. While the steps do not change, these subsystems can vary in their actual implementation. One variant of block sort allows it to use any amount of additional memory provided to it, by using this ''external buffer'' for merging an A subarray or A block with B whenever A fits into it. In this situation it would be identical to a merge sort. Good choices for the buffer size include: Rather than tagging the A blocks using the contents of one of the internal buffers, an indirect ''movement-imitation buffer'' can be used instead. This is an internal buffer defined as ''s1 t s2'', where ''s1'' and ''s2'' are each as large as the number of A and B blocks, and ''t'' contains any values immediately following ''s1'' that are equal to the last value of ''s1'' (thus ensuring that no value in ''s2'' appears in ''s1''). A second internal buffer containing unique values is still used. The first values of ''s1'' and ''s2'' are then swapped with each other to encode information into the buffer about which blocks are A blocks and which are B blocks. When an A block at index ''i'' is swapped with a B block at index ''j'' (where the first evenly sized A block is initially at index 0), s1 and s1 are swapped with s2 and s2 respectively. This ''imitates the movements'' of the A blocks through B. The unique values in the second buffer are used to determine the original order of the A blocks as they are rolled through the B blocks. Once all of the A blocks have been dropped, the movement-imitation buffer is used to decode whether a given block in the array is an A block or a B block, each A block is rotated into B, and the second internal buffer is used as swap space for the local merges. The ''second'' value of each A block doesn't necessarily need to be tagged – the first, last, or any other element could be used instead. However, if the first value is tagged, the values will need to be read from the first internal buffer (where they were swapped) when deciding where to drop the minimum A block. Many sorting algorithms can be used to sort the contents of the second internal buffer, including unstable sorts likequicksort
Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961, it is still a commonly used algorithm for sorting. Overall, it is slightly faster than ...
, since the contents of the buffer are guaranteed to unique. Insertion sort is still recommended, though, for its situational performance and lack of recursion.
Analysis
Block sort is a well-defined and testable class of algorithms, with working implementations available as a merge and as a sort. This allows its characteristics to be measured and considered.Complexity
Block sort begins by performing insertion sort on groups of 16–31 items in the array. Insertion sort is an operation, so this leads to anywhere from to , which is once the constant factors are omitted. It must also apply an insertion sort on the second internal buffer after each level of merging is completed. However, as this buffer was limited to in size, the operation also ends up being . Next it must extract two internal buffers for each level of the merge sort. It does so by iterating over the items in the A and B subarrays and incrementing a counter whenever the value changes, and upon finding enough values it rotates them to the start of A or the end of B. In the worst case this will end up searching the entire array before finding non-contiguous unique values, which requires comparisons and rotations for values. This resolves to , or . When none of the A or B subarrays contained unique values to create the internal buffers, a normally suboptimal in-place merge operation is performed where it repeatedly binary searches and rotates A into B. However, the known lack of unique values within any of the subarrays places a hard limit on the number of binary searches and rotations that will be performed during this step, which is again items rotated up to times, or . The size of each block is also adjusted to be smaller in the case where it found unique values but not 2, which further limits the number of unique values contained within any A or B block. Tagging the A blocks is performed times for each A subarray, then the A blocks are rolled through and inserted into the B blocks up to times. The local merges retain the same complexity of a standard merge, albeit with more assignments since the values must be swapped rather than copied. The linear search for finding the new minimum A block iterates over blocks times. And the buffer redistribution process is identical to the buffer extraction but in reverse, and therefore has the same complexity. After omitting all but the highest complexity and considering that there are levels in the outer merge loop, this leads to a final asymptotic complexity of for the worst and average cases. For the best case, where the data is already in order, the merge step performs comparisons for the first level, then , , , etc. This is a well-known mathematical series which resolves to .Memory
As block sort is non-recursive and does not require the use of dynamic allocations, this leads to constantstack
Stack may refer to:
Places
* Stack Island, an island game reserve in Bass Strait, south-eastern Australia, in Tasmania’s Hunter Island Group
* Blue Stack Mountains, in Co. Donegal, Ireland
People
* Stack (surname) (including a list of people ...
and heap space. It uses O(1) auxiliary memory in a transdichotomous model In computational complexity theory, and more specifically in the analysis of algorithms with integer data, the transdichotomous model is a variation of the random access machine in which the machine word size is assumed to match the problem size. ...
, which accepts that the O(log ''n'') bits needed to keep track of the ranges for A and B cannot be any greater than 32 or 64 on 32-bit or 64-bit computing systems, respectively, and therefore simplifies to O(1) space for any array that can feasibly be allocated.
Stability
Although items in the array are moved out of order during a block sort, each operation is fully reversible and will have restored the original order of equivalent items by its completion. Stability requires the first instance of each value in an array before sorting to still be the first instance of that value after sorting. Block sort moves these first instances to the start of the array to create the two internal buffers, but when all of the merges are completed for the current level of the block sort, those values are distributed back to the first sorted position within the array. This maintains stability. Before rolling the A blocks through the B blocks, each A block has its second value swapped with a value from the first buffer. At that point the A blocks are moved out of order to roll through the B blocks. However, once it finds where it should insert the smallest A block into the previous B block, that smallest A block is moved back to the start of the A blocks and its second value is restored. By the time all of the A blocks have been inserted, the A blocks will be in order again and the first buffer will contain its original values in the original order. Using the second buffer as swap space when merging an A block with some B values causes the contents of that buffer to be rearranged. However, as the algorithm already ensured the buffer only contains unique values, sorting the contents of the buffer is sufficient to restore their original stable order.Adaptivity
Block sort is anadaptive sort A sorting algorithm falls into the adaptive sort family if it takes advantage of existing order in its input. It benefits from the presortedness in the input sequence – or a limited amount of disorder for various definitions of measures of disord ...
on two levels: first, it skips merging A and B subarrays that are already in order. Next, when A and B need to be merged and are broken into evenly sized blocks, the A blocks are only rolled through B as far as is necessary, and each block is only merged with the B values immediately following it. The more ordered the data originally was, the fewer B values there will be that need to be merged into A.
Advantages
Block sort is a stable sort that does not require additional memory, which is useful in cases where there is not enough free memory to allocate the O(n) buffer. When using the ''external buffer'' variant of block sort, it can scale from using O(n) memory to progressively smaller buffers as needed, and will still work efficiently within those constraints.Disadvantages
Block sort does not exploit sorted ranges of data on as fine a level as some other algorithms, such asTimsort
Timsort is a hybrid, stable sorting algorithm, derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It was implemented by Tim Peters in 2002 for use in the Python programming language. The algorit ...
. It only checks for these sorted ranges at the two predefined levels: the A and B subarrays, and the A and B blocks. It is also harder to implement and parallelize compared to a merge sort.
References
{{sorting Sorting algorithms Comparison sorts Stable sorts Articles with example pseudocode