Bicorn on:
[Wikipedia]
[Google]
[Amazon]
 In
In
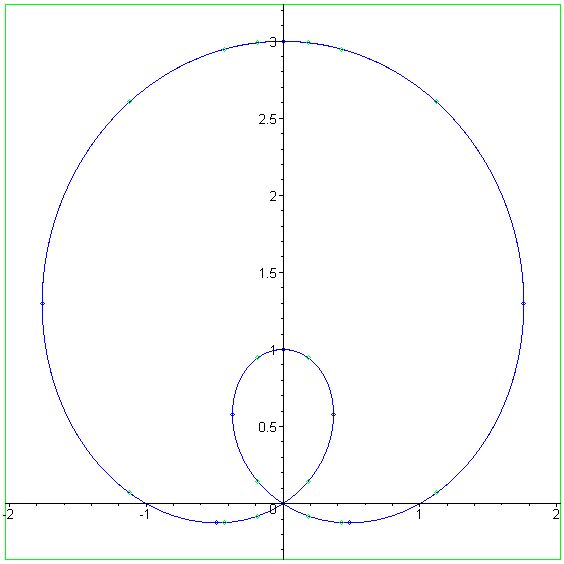 The bicorn is a
The bicorn is a
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne
The bicorne or bicorn (two-cornered) is a historical form of hat widely adopted in the 1790s as an item of uniform by European and American army and naval officers. Most generals and staff officers of the Napoleonic period wore bicornes, wh ...
, is a rational
Rationality is the quality of being guided by or based on reasons. In this regard, a person acts rationally if they have a good reason for what they do or a belief is rational if it is based on strong evidence. This quality can apply to an abil ...
quartic curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:
:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0,
with at least one o ...
defined by the equation
It has two cusps and is symmetric about the y-axis.
History
In 1864,James Joseph Sylvester
James Joseph Sylvester (3 September 1814 – 15 March 1897) was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory, and combinatorics. He played a leadership ...
studied the curve
in connection with the classification of quintic equation
In algebra, a quintic function is a function of the form
:g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\,
where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a ...
s; he named the curve a bicorn because it has two cusps. This curve was further studied by Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a prolific British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics.
As a child, Cayley enjoyed solving complex maths problems ...
in 1867.
Properties
 The bicorn is a
The bicorn is a plane algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane ...
of degree four and genus
Genus ( plural genera ) is a taxonomic rank used in the biological classification of living and fossil organisms as well as viruses. In the hierarchy of biological classification, genus comes above species and below family. In binomial n ...
zero. It has two cusp singularities in the real plane, and a double point in the complex projective plane
In mathematics, the complex projective plane, usually denoted P2(C), is the two-dimensional complex projective space. It is a complex manifold of complex dimension 2, described by three complex coordinates
:(Z_1,Z_2,Z_3) \in \mathbf^3,\qquad (Z_1 ...
at x=0, z=0. If we move x=0 and z=0 to the origin substituting and perform an imaginary rotation on x bu substituting ix/z for x and 1/z for y in the bicorn curve, we obtain
This curve, a limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. I ...
, has an ordinary double point at the origin, and two nodes in the complex plane, at and .
The parametric equations of a bicorn curve are and with .
See also
*List of curves
This is a list of Wikipedia articles about curves used in different fields: mathematics (including geometry, statistics, and applied mathematics), physics, engineering, economics, medicine, biology, psychology, ecology, etc.
Mathematics (Geometr ...
References
External links
* {{MathWorld, title=Bicorn, urlname=Bicorn Plane curves Algebraic curves