Betti Numbers on:
[Wikipedia]
[Google]
[Amazon]
In
 Informally, the ''k''th Betti number refers to the number of ''k''-dimensional ''holes'' on a topological surface. A "''k''-dimensional ''hole''" is a ''k''-dimensional cycle that is not a boundary of a (''k''+1)-dimensional object.
The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:
* ''b''0 is the number of connected components;
* ''b''1 is the number of one-dimensional or "circular" holes;
* ''b''2 is the number of two-dimensional "voids" or "cavities".
Thus, for example, a torus has one connected surface component so ''b''0 = 1, two "circular" holes (one equatorial and one meridional) so ''b''1 = 2, and a single cavity enclosed within the surface so ''b''2 = 1.
Another interpretation of ''b''k is the maximum number of ''k''-dimensional curves that can be removed while the object remains connected. For example, the torus remains connected after removing two 1-dimensional curves (equatorial and meridional) so ''b''1 = 2.
The two-dimensional Betti numbers are easier to understand because we can see the world in 0, 1, 2, and 3-dimensions.
Informally, the ''k''th Betti number refers to the number of ''k''-dimensional ''holes'' on a topological surface. A "''k''-dimensional ''hole''" is a ''k''-dimensional cycle that is not a boundary of a (''k''+1)-dimensional object.
The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:
* ''b''0 is the number of connected components;
* ''b''1 is the number of one-dimensional or "circular" holes;
* ''b''2 is the number of two-dimensional "voids" or "cavities".
Thus, for example, a torus has one connected surface component so ''b''0 = 1, two "circular" holes (one equatorial and one meridional) so ''b''1 = 2, and a single cavity enclosed within the surface so ''b''2 = 1.
Another interpretation of ''b''k is the maximum number of ''k''-dimensional curves that can be removed while the object remains connected. For example, the torus remains connected after removing two 1-dimensional curves (equatorial and meridional) so ''b''1 = 2.
The two-dimensional Betti numbers are easier to understand because we can see the world in 0, 1, 2, and 3-dimensions.
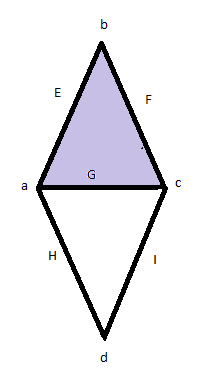 Consider a simplicial complex with 0-simplices: a, b, c, and d, 1-simplices: E, F, G, H and I, and the only 2-simplex is J, which is the shaded region in the figure. It is clear that there is one connected component in this figure (''b''0); one hole, which is the unshaded region (''b''1); and no "voids" or "cavities" (''b''2).
This means that the rank of is 1, the rank of is 1 and the rank of is 0.
The Betti number sequence for this figure is 1, 1, 0, 0, ...; the Poincaré polynomial is .
Consider a simplicial complex with 0-simplices: a, b, c, and d, 1-simplices: E, F, G, H and I, and the only 2-simplex is J, which is the shaded region in the figure. It is clear that there is one connected component in this figure (''b''0); one hole, which is the unshaded region (''b''1); and no "voids" or "cavities" (''b''2).
This means that the rank of is 1, the rank of is 1 and the rank of is 0.
The Betti number sequence for this figure is 1, 1, 0, 0, ...; the Poincaré polynomial is .
algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify ...
, the Betti numbers are used to distinguish topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called po ...
s based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually cons ...
s (such as compact manifold
In mathematics, a closed manifold is a manifold without boundary that is compact.
In comparison, an open manifold is a manifold without boundary that has only ''non-compact'' components.
Examples
The only connected one-dimensional example is ...
s, finite simplicial complexes
In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their ''n''-dimensional counterparts (see illustration). Simplicial complexes should not be confused with the more abstract notion of a simplicial se ...
or CW complexes
A CW complex (also called cellular complex or cell complex) is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead (open access) to meet the needs of homotopy theory. This cl ...
), the sequence of Betti numbers is 0 from some point onward (Betti numbers vanish above the dimension of a space), and they are all finite.
The ''n''th Betti number represents the rank
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* ...
of the ''n''th homology group
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topolog ...
, denoted ''H''''n'', which tells us the maximum number of cuts that can be made before separating a surface into two pieces or 0-cycles, 1-cycles, etc. For example, if then , if then , if then , if then , etc. Note that only the ranks of infinite groups are considered, so for example if , where is the finite cyclic group of order 2, then . These finite components of the homology groups are their torsion subgroup In the theory of abelian groups, the torsion subgroup ''AT'' of an abelian group ''A'' is the subgroup of ''A'' consisting of all elements that have finite order (the torsion elements of ''A''). An abelian group ''A'' is called a torsion group (or ...
s, and they are denoted by torsion coefficients.
The term "Betti numbers" was coined by Henri Poincaré after Enrico Betti
Enrico Betti Glaoui (21 October 1823 – 11 August 1892) was an Italian mathematician, now remembered mostly for his 1871 paper on topology that led to the later naming after him of the Betti numbers. He worked also on the theory of equations, giv ...
. The modern formulation is due to Emmy Noether
Amalie Emmy NoetherEmmy is the '' Rufname'', the second of two official given names, intended for daily use. Cf. for example the résumé submitted by Noether to Erlangen University in 1907 (Erlangen University archive, ''Promotionsakt Emmy Noeth ...
. Betti numbers are used today in fields such as simplicial homology In algebraic topology, simplicial homology is the sequence of homology groups of a simplicial complex. It formalizes the idea of the number of holes of a given dimension in the complex. This generalizes the number of connected components (the case ...
, computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includi ...
, digital images, etc.
Geometric interpretation
 Informally, the ''k''th Betti number refers to the number of ''k''-dimensional ''holes'' on a topological surface. A "''k''-dimensional ''hole''" is a ''k''-dimensional cycle that is not a boundary of a (''k''+1)-dimensional object.
The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:
* ''b''0 is the number of connected components;
* ''b''1 is the number of one-dimensional or "circular" holes;
* ''b''2 is the number of two-dimensional "voids" or "cavities".
Thus, for example, a torus has one connected surface component so ''b''0 = 1, two "circular" holes (one equatorial and one meridional) so ''b''1 = 2, and a single cavity enclosed within the surface so ''b''2 = 1.
Another interpretation of ''b''k is the maximum number of ''k''-dimensional curves that can be removed while the object remains connected. For example, the torus remains connected after removing two 1-dimensional curves (equatorial and meridional) so ''b''1 = 2.
The two-dimensional Betti numbers are easier to understand because we can see the world in 0, 1, 2, and 3-dimensions.
Informally, the ''k''th Betti number refers to the number of ''k''-dimensional ''holes'' on a topological surface. A "''k''-dimensional ''hole''" is a ''k''-dimensional cycle that is not a boundary of a (''k''+1)-dimensional object.
The first few Betti numbers have the following definitions for 0-dimensional, 1-dimensional, and 2-dimensional simplicial complexes:
* ''b''0 is the number of connected components;
* ''b''1 is the number of one-dimensional or "circular" holes;
* ''b''2 is the number of two-dimensional "voids" or "cavities".
Thus, for example, a torus has one connected surface component so ''b''0 = 1, two "circular" holes (one equatorial and one meridional) so ''b''1 = 2, and a single cavity enclosed within the surface so ''b''2 = 1.
Another interpretation of ''b''k is the maximum number of ''k''-dimensional curves that can be removed while the object remains connected. For example, the torus remains connected after removing two 1-dimensional curves (equatorial and meridional) so ''b''1 = 2.
The two-dimensional Betti numbers are easier to understand because we can see the world in 0, 1, 2, and 3-dimensions.
Formal definition
For a non-negativeinteger
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
''k'', the ''k''th Betti number ''b''''k''(''X'') of the space ''X'' is defined as the rank
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* ...
(number of linearly independent generators) of the abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is comm ...
''H''''k''(''X''), the ''k''th homology group
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topolog ...
of ''X''. The ''k''th homology group is , the s are the boundary maps of the simplicial complex and the rank of Hk is the ''k''th Betti number. Equivalently, one can define it as the vector space dimension
In mathematics, the dimension of a vector space ''V'' is the cardinality (i.e., the number of vectors) of a Basis (linear algebra), basis of ''V'' over its base Field (mathematics), field. p. 44, §2.36 It is sometimes called Hamel dimension (after ...
of ''H''''k''(''X''; Q) since the homology group in this case is a vector space over Q. The universal coefficient theorem
In algebraic topology, universal coefficient theorems establish relationships between homology groups (or cohomology groups) with different coefficients. For instance, for every topological space , its ''integral homology groups'':
:
completely ...
, in a very simple torsion-free case, shows that these definitions are the same.
More generally, given a field
Field may refer to:
Expanses of open ground
* Field (agriculture), an area of land used for agricultural purposes
* Airfield, an aerodrome that lacks the infrastructure of an airport
* Battlefield
* Lawn, an area of mowed grass
* Meadow, a grass ...
''F'' one can define ''b''''k''(''X'', ''F''), the ''k''th Betti number with coefficients in ''F'', as the vector space dimension of ''H''''k''(''X'', ''F'').
Poincaré polynomial
The Poincaré polynomial of a surface is defined to be the generating function of its Betti numbers. For example, the Betti numbers of the torus are 1, 2, and 1; thus its Poincaré polynomial is . The same definition applies to any topological space which has a finitely generated homology. Given a topological space which has a finitely generated homology, the Poincaré polynomial is defined as the generating function of its Betti numbers, via the polynomial where the coefficient of is .Examples
Betti numbers of a graph
Consider a topological graph ''G'' in which the set of vertices is ''V'', the set of edges is ''E'', and the set of connected components is ''C''. As explained in the page ongraph homology In algebraic topology and graph theory, graph homology describes the homology groups of a graph, where the graph is considered as a topological space. It formalizes the idea of the number of "holes" in the graph. It is a special case of a simplic ...
, its homology groups are given by:
:
This may be proved straightforwardly by mathematical induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help ...
on the number of edges. A new edge either increments the number of 1-cycles or decrements the number of connected components.
Therefore, the "zero-th" Betti number ''b''0(''G'') equals , ''C'', , which is simply the number of connected components.
The first Betti number ''b''1(''G'') equals , ''E'', + , ''C'', - , ''V'', . It is also called the cyclomatic number
In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or fo ...
—a term introduced by Gustav Kirchhoff
Gustav Robert Kirchhoff (; 12 March 1824 – 17 October 1887) was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects.
He ...
before Betti's paper. See cyclomatic complexity
Cyclomatic complexity is a software metric used to indicate the complexity of a program. It is a quantitative measure of the number of linearly independent paths through a program's source code. It was developed by Thomas J. McCabe, Sr. in 1976. ...
for an application to software engineering
Software engineering is a systematic engineering approach to software development.
A software engineer is a person who applies the principles of software engineering to design, develop, maintain, test, and evaluate computer software. The term '' ...
.
All other Betti numbers are 0.
Betti numbers of a simplicial complex
 Consider a simplicial complex with 0-simplices: a, b, c, and d, 1-simplices: E, F, G, H and I, and the only 2-simplex is J, which is the shaded region in the figure. It is clear that there is one connected component in this figure (''b''0); one hole, which is the unshaded region (''b''1); and no "voids" or "cavities" (''b''2).
This means that the rank of is 1, the rank of is 1 and the rank of is 0.
The Betti number sequence for this figure is 1, 1, 0, 0, ...; the Poincaré polynomial is .
Consider a simplicial complex with 0-simplices: a, b, c, and d, 1-simplices: E, F, G, H and I, and the only 2-simplex is J, which is the shaded region in the figure. It is clear that there is one connected component in this figure (''b''0); one hole, which is the unshaded region (''b''1); and no "voids" or "cavities" (''b''2).
This means that the rank of is 1, the rank of is 1 and the rank of is 0.
The Betti number sequence for this figure is 1, 1, 0, 0, ...; the Poincaré polynomial is .
Betti numbers of the projective plane
The homology groups of theprojective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that d ...
''P'' are:
:
Here, Z2 is the cyclic group
In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bina ...
of order 2. The 0-th Betti number is again 1. However, the 1-st Betti number is 0. This is because ''H''1(''P'') is a finite group - it does not have any infinite component. The finite component of the group is called the torsion coefficient of ''P''. The (rational) Betti numbers ''b''''k''(''X'') do not take into account any torsion
Torsion may refer to:
Science
* Torsion (mechanics), the twisting of an object due to an applied torque
* Torsion of spacetime, the field used in Einstein–Cartan theory and
** Alternatives to general relativity
* Torsion angle, in chemistry
Bi ...
in the homology groups, but they are very useful basic topological invariants. In the most intuitive terms, they allow one to count the number of ''holes'' of different dimensions.
Properties
Euler characteristic
For a finite CW-complex ''K'' we have : where denotes Euler characteristic of ''K'' and any field ''F''.Cartesian product
For any two spaces ''X'' and ''Y'' we have : where denotes the Poincaré polynomial of ''X'', (more generally, theHilbert–Poincaré series
In mathematics, and in particular in the field of algebra, a Hilbert–Poincaré series (also known under the name Hilbert series), named after David Hilbert and Henri Poincaré, is an adaptation of the notion of dimension to the context of grade ...
, for infinite-dimensional spaces), i.e., the generating function of the Betti numbers of ''X'':
:
see Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem, also called a Künneth formula, is a statement relating the homology of two objects to the homology of their product. The classical statement of the K� ...
.
Symmetry
If ''X'' is ''n''-dimensional manifold, there is symmetry interchanging and , for any : : under conditions (a ''closed'' and ''oriented'' manifold); seePoincaré duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds. It states that if ''M'' is an ''n''-dimensional oriented closed manifold (compact ...
.
Different coefficients
The dependence on the field ''F'' is only through its characteristic. If the homology groups are torsion-free, the Betti numbers are independent of ''F''. The connection of ''p''-torsion and the Betti number for characteristic ''p'', for ''p'' a prime number, is given in detail by theuniversal coefficient theorem
In algebraic topology, universal coefficient theorems establish relationships between homology groups (or cohomology groups) with different coefficients. For instance, for every topological space , its ''integral homology groups'':
:
completely ...
(based on Tor functor
In mathematics, the Tor functors are the derived functors of the tensor product of modules over a ring. Along with the Ext functor, Tor is one of the central concepts of homological algebra, in which ideas from algebraic topology are used to con ...
s, but in a simple case).
More examples
# The Betti number sequence for a circle is 1, 1, 0, 0, 0, ...; #: the Poincaré polynomial is #:: . # The Betti number sequence for a three-torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
If the axis of revolution does not tou ...
is 1, 3, 3, 1, 0, 0, 0, ... .
#: the Poincaré polynomial is
#:: .
# Similarly, for an ''n''-torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
If the axis of revolution does not tou ...
,
#: the Poincaré polynomial is
#:: (by the Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem, also called a Künneth formula, is a statement relating the homology of two objects to the homology of their product. The classical statement of the K� ...
), so the Betti numbers are the binomial coefficients.
It is possible for spaces that are infinite-dimensional in an essential way to have an infinite sequence of non-zero Betti numbers. An example is the infinite-dimensional complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a ...
, with sequence 1, 0, 1, 0, 1, ... that is periodic, with period length
A periodic function is a Function (mathematics), function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used th ...
2.
In this case the Poincaré function is not a polynomial but rather an infinite series
:,
which, being a geometric series, can be expressed as the rational function
:
More generally, any sequence that is periodic can be expressed as a sum of geometric series, generalizing the above. For example has the generating function
:
and more generally linear recursive sequence
In mathematics and theoretical computer science, a constant-recursive sequence is an infinite sequence of numbers where each number in the sequence is equal to a fixed linear combination of one or more of its immediate predecessors. A constant ...
s are exactly the sequences generated by rational functions
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rat ...
; thus the Poincaré series is expressible as a rational function if and only if the sequence of Betti numbers is a linear recursive sequence.
The Poincaré polynomials of the compact simple Lie groups
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additi ...
are:
:
Relationship with dimensions of spaces of differential forms
In geometric situations when is a closed manifold, the importance of the Betti numbers may arise from a different direction, namely that they predict the dimensions of vector spaces ofclosed differential form In mathematics, especially vector calculus and differential topology, a closed form is a differential form ''α'' whose exterior derivative is zero (), and an exact form is a differential form, ''α'', that is the exterior derivative of another diff ...
s '' modulo'' exact differential form In mathematics, especially vector calculus and differential topology, a closed form is a differential form ''α'' whose exterior derivative is zero (), and an exact form is a differential form, ''α'', that is the exterior derivative of another diff ...
s. The connection with the definition given above is via three basic results, de Rham's theorem and Poincaré duality
In mathematics, the Poincaré duality theorem, named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds. It states that if ''M'' is an ''n''-dimensional oriented closed manifold (compact ...
(when those apply), and the universal coefficient theorem
In algebraic topology, universal coefficient theorems establish relationships between homology groups (or cohomology groups) with different coefficients. For instance, for every topological space , its ''integral homology groups'':
:
completely ...
of homology theory.
There is an alternate reading, namely that the Betti numbers give the dimensions of spaces of harmonic form
In mathematics, Hodge theory, named after W. V. D. Hodge, is a method for studying the cohomology groups of a smooth manifold ''M'' using partial differential equations. The key observation is that, given a Riemannian metric on ''M'', every coh ...
s. This requires the use of some of the results of Hodge theory on the Hodge Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is th ...
.
In this setting, Morse theory
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiab ...
gives a set of inequalities for alternating sums of Betti numbers in terms of a corresponding alternating sum of the number of critical points of a Morse function
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiab ...
of a given index:
:
Edward Witten
Edward Witten (born August 26, 1951) is an American mathematical and theoretical physicist. He is a Professor Emeritus in the School of Natural Sciences at the Institute for Advanced Study in Princeton. Witten is a researcher in string theory, q ...
gave an explanation of these inequalities by using the Morse function to modify the exterior derivative in the de Rham complex
In mathematics, de Rham cohomology (named after Georges de Rham) is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly ada ...
.
See also
*Topological data analysis
In applied mathematics, topological based data analysis (TDA) is an approach to the analysis of datasets using techniques from topology. Extraction of information from datasets that are high-dimensional, incomplete and noisy is generally challengin ...
* Torsion coefficient
A torsion spring is a spring that works by twisting its end along its axis; that is, a flexible elastic object that stores mechanical energy when it is twisted. When it is twisted, it exerts a torque in the opposite direction, proportiona ...
* Euler characteristic
References
*. *. {{DEFAULTSORT:Betti Number Algebraic topology Graph invariants Topological graph theory Generating functions