Beltrami identity

The Beltrami identity, named after Eugenio Beltrami, is a special case of the Euler–Lagrange equation in the calculus of variations.

The Euler–Lagrange equation serves to extremize action functionals of the form

:I \int_a^b L ,u(x),u'(x)\, dx \, ,

where $a$ and $b$ are constants and $u'(x) = \frac$.

If $\frac = 0$, then the Euler–Lagrange equation reduces to the Beltrami identity,

where is a constant.Weisstein, Eric W
"Euler-Lagrange Differential Equation."
Fro
MathWorld
-A Wolfram Web Resource. See Eq. (5).Thus, the Legendre transform of the Lagrangian, the Hamiltonian, is constant along the dynamical path.

Derivation

By the chain rule, the derivative of is
:$\frac = \frac \frac + \frac \frac + \frac \frac \, .$
Because $\frac = 0$, we write
:$\frac = \frac u' + \frac u'' \, .$
We have an expression for $\frac$ from the Euler–Lagrange equation,
:$\frac = \frac \frac \,$
that we can substitute in the above expression for $\frac$ to obtain
:$\frac =u'\frac \frac + u''\frac \, .$
By the product rule, the right side is equivalent to
:$\frac = \frac \left( u' \frac \right) \, .$
By integrating both sides and putting both terms on one side, we get the Beltrami identity,
:$L - u'\frac = C \, .$

Applications

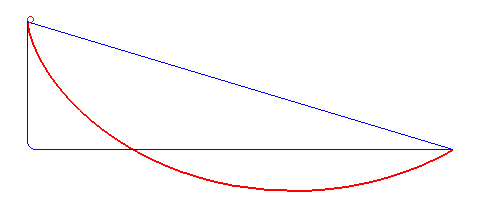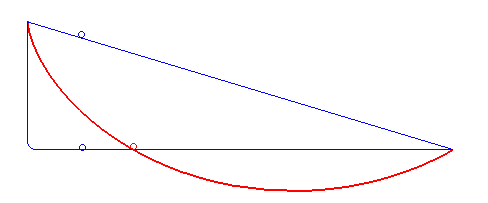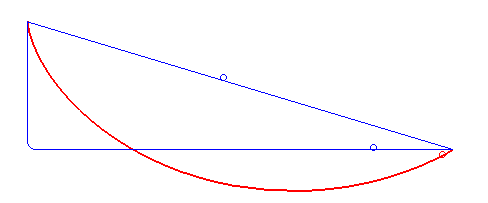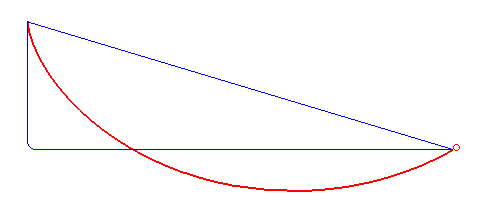
Solution to the brachistochrone problem

An example of an application of the Beltrami identity is the brachistochrone problem, which involves finding the curve $y = y(x)$ that minimizes the integral

: I = \int_0^a \sqrt dx \, .

The integrand
:$L(y,y') = \sqrt$
does not depend explicitly on the variable of integration $x$, so the Beltrami identity applies,
:$L-y'\frac=C \, .$
Substituting for $L$ and simplifying,
:$y(1+y'^) = 1/C^2 ~~\text \, ,$
which can be solved with the result put in the form of parametric equations
:$x = A(\phi - \sin \phi)$
:$y = A(1 - \cos \phi)$
with $A$ being half the above constant, $\frac$, and $\phi$ being a variable. These are the parametric equations for a cycloid.This solution of the Brachistochrone problem corresponds to the one in —

Solution to the catenary problem

Consider a string with uniform density $\mu$ of length $l$ suspended from two points of equal height and at distance $D$. By the formula for arc length,
$l = \int_S dS = \int_^ \sqrtdx,$
where $S$ is the path of the string, and $s_1$ and $s_2$ are the boundary conditions.

The curve has to minimize its potential energy
$U = \int_S g\mu y\cdot dS = \int_^ g\mu y\sqrt dx,$
and is subject to the constraint
$\int_^ \sqrt dx = l ,$
where $g$ is the force of gravity.

Because the independent variable $x$ does not appear in the integrand, the Beltrami identity may be used to express the path of the string as a separable first order differential equation

L - y\prime \frac = \mu gy\sqrt + \lambda \sqrt - \left mu gy\frac + \lambda \frac\right= C,
where $\lambda$ is the Lagrange multiplier.

It is possible to simplify the differential equation as such:
$\frac = C.$

Solving this equation gives the hyperbolic cosine, where $C_0$ is a second constant obtained from integration

y = \frac\cosh \left \frac (x + C_0) \right- \frac.

The three unknowns $C$, $C_0$, and $\lambda$ can be solved for using the constraints for the string's endpoints and arc length $l$, though a closed-form solution is often very difficult to obtain.

Notes

References

{{reflist

Calculus of variations
Optimal control