arithmetic overflow on:
[Wikipedia]
[Google]
[Amazon]
 In
In
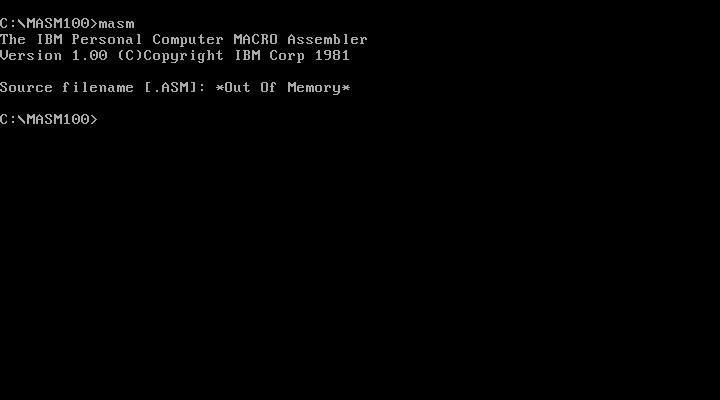 IBM– Microsoft Macro Assembler (MASM) version 1.00, and likely all other programs built by the same Pascal compiler, had an integer overflow and signedness error in the stack setup code, which prevented them from running on newer DOS machines or emulators under some common configurations with more than 512 KiB of memory. The program either hangs or displays an error message and exits to DOS.
In August 2016, a
IBM– Microsoft Macro Assembler (MASM) version 1.00, and likely all other programs built by the same Pascal compiler, had an integer overflow and signedness error in the stack setup code, which prevented them from running on newer DOS machines or emulators under some common configurations with more than 512 KiB of memory. The program either hangs or displays an error message and exits to DOS.
In August 2016, a
Phrack #60, Basic Integer Overflows
* ttps://web.archive.org/web/20121010025025/http://www.cs.cmu.edu/~dbrumley/pubs/integer-ndss-07.pdf Efficient and Accurate Detection of Integer-based Attacksbr>WASC Threat Classification – Integer OverflowsUnderstanding Integer Overflow in C/C++Binary Overflow – Binary ArithmeticISO C11 Standard
Software bugs Computer security exploits Computer arithmetic de:Arithmetischer Überlauf
 In
In computer programming
Computer programming or coding is the composition of sequences of instructions, called computer program, programs, that computers can follow to perform tasks. It involves designing and implementing algorithms, step-by-step specifications of proc ...
, an integer overflow occurs when an arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
operation on integers attempts to create a numeric value that is outside of the range that can be represented with a given number of digits – either higher than the maximum or lower than the minimum representable value.
The most common result of an overflow is that the least significant representable digits of the result are stored; the result is said to ''wrap'' around the maximum (i.e. modulo
In computing and mathematics, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another, the latter being called the '' modulus'' of the operation.
Given two positive numbers and , mo ...
a power of the radix, usually two in modern computers, but sometimes ten or other number). On some processors like graphics processing units (GPUs) and digital signal processors (DSPs) which support saturation arithmetic, overflowed results would be ''clamped'', i.e. set to the minimum value in the representable range if the result is below the minimum and set to the maximum value in the representable range if the result is above the maximum, rather than wrapped around.
An overflow condition may give results leading to unintended behavior. In particular, if the possibility has not been anticipated, overflow can compromise a program's reliability and security.
For some applications, such as timers and clocks, wrapping on overflow can be desirable. The C11 standard states that for unsigned integers, modulo wrapping is the defined behavior and the term overflow never applies: "a computation involving unsigned operands can never overflow."
Origin
The register width of a processor determines the range of values that can be represented in its registers. Though the vast majority of computers can perform multiple-precision arithmetic on operands in memory, allowing numbers to be arbitrarily long and overflow to be avoided, the register width limits the sizes of numbers that can be operated on (e.g., added or subtracted) using a single instruction per operation. Typical binary register widths for unsigned integers include: * 4-bit: maximum representable value 24 − 1 = 15 * 8-bit: maximum representable value 28 − 1 = 255 *16-bit
16-bit microcomputers are microcomputers that use 16-bit microprocessors.
A 16-bit register can store 216 different values. The range of integer values that can be stored in 16 bits depends on the integer representation used. With the two ...
: maximum representable value 216 − 1 = 65,535
* 32-bit: maximum representable value 232 − 1 = 4,294,967,295 (the most common width for personal computers ),
* 64-bit: maximum representable value 264 − 1 = 18,446,744,073,709,551,615 (the most common width for personal computer central processing unit
A central processing unit (CPU), also called a central processor, main processor, or just processor, is the primary Processor (computing), processor in a given computer. Its electronic circuitry executes Instruction (computing), instructions ...
s (CPUs), ),
* 128-bit: maximum representable value 2128 − 1 = 340,282,366,920,938,463,463,374,607,431,768,211,455
When an unsigned arithmetic operation produces a result larger than the maximum above for an N-bit integer, an overflow reduces the result to modulo
In computing and mathematics, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another, the latter being called the '' modulus'' of the operation.
Given two positive numbers and , mo ...
N-th power of 2, retaining only the least significant bits of the result and effectively causing a ''wrap around''.
In particular, multiplying or adding two integers may result in a value that is unexpectedly small, and subtracting from a small integer may cause a wrap to a large positive value (for example, 8-bit integer addition 255 + 2 results in 1, which is , and similarly subtraction 0 − 1 results in 255, a two's complement representation of −1).
Such wraparound may cause security detriments—if an overflowed value is used as the number of bytes to allocate for a buffer, the buffer will be allocated unexpectedly small, potentially leading to a buffer overflow which, depending on the use of the buffer, might in turn cause arbitrary code execution.
If the variable has a signed integer type, a program may make the assumption that a variable always contains a positive value. An integer overflow can cause the value to wrap and become negative, which violates the program's assumption and may lead to unexpected behavior (for example, 8-bit integer addition of 127 + 1 results in −128, a two's complement of 128). (A solution for this particular problem is to use unsigned integer types for values that a program expects and assumes will never be negative.)
Flags
Most computers have two dedicated processor flags to check for overflow conditions. The carry flag is set when the result of an addition or subtraction, considering the operands and result as unsigned numbers, does not fit in the given number of bits. This indicates an overflow with a ''carry'' or ''borrow'' from the most significant bit. An immediately following ''add with carry'' or ''subtract with borrow'' operation would use the contents of this flag to modify a register or a memory location that contains the higher part of a multi-word value. The overflow flag is set when the result of an operation on signed numbers does not have the sign that one would predict from the signs of the operands, e.g., a negative result when adding two positive numbers. This indicates that an overflow has occurred and the signed result represented in two's complement form would not fit in the given number of bits.Definition variations and ambiguity
For an unsigned type, when the ideal result of an operation is outside the type's representable range and the returned result is obtained by wrapping, then this event is commonly defined as an overflow. In contrast, the C11 standard defines that this event is not an overflow and states "a computation involving unsigned operands can never overflow." When the ideal result of an integer operation is outside the type's representable range and the returned result is obtained by clamping, then this event is commonly defined as a saturation. Use varies as to whether a saturation is or is not an overflow. To eliminate ambiguity, the terms wrapping overflow and saturating overflow can be used. Many references can be found to integer underflow. When the term integer underflow is used, it means the ideal result was closer to negative infinity than the output type's representable value closest to negative infinity. Depending on context, the definition of overflow may include all types including underflows, or it may only include cases where the ideal result was closer to positive infinity than the output type's representable value closest to positive infinity. When the ideal result of an operation is not an exact integer, the meaning of overflow can be ambiguous in edge cases. Consider the case where the ideal result has a value of 127.25 and the output type's maximum representable value is 127. If overflow is defined as the ideal value being outside the representable range of the output type, then this case would be classified as an overflow. For operations that have well defined rounding behavior, overflow classification may need to be postponed until after rounding is applied. The C11 standard defines that conversions from floating point to integer must round toward zero. If C is used to convert the floating point value 127.25 to integer, then rounding should be applied first to give an ideal integer output of 127. Since the rounded integer is in the outputs range, the C standard would not classify this conversion as an overflow.Inconsistent behavior
The behavior on occurrence of overflow may not be consistent in all circumstances. For example, in the language Rust, while functionality is provided to give users choice and control, the behavior for basic use of mathematic operators is naturally fixed; however, this fixed behavior differs between a program built in 'debug' mode and one built in 'release' mode. In C, unsigned integer overflow is defined to wrap around, while signed integer overflow causes undefined behavior.Methods to address integer overflow problems
Detection
Run-time overflow detection implementationUBSan ( undefined behavior sanitizer) is available for C compilers.
In Java 8, there are overloaded methods, for example , which will throw an in case of overflow.
Computer emergency response team (CERT) developed the As-if Infinitely Ranged (AIR) integer model, a largely automated mechanism to eliminate integer overflow and truncation in C/C++ using run-time error handling.
Avoidance
By allocating variables with data types that are large enough to contain all values that may possibly be computed and stored in them, it is always possible to avoid overflow. Even when the available space or the fixed data types provided by a programming language or environment are too limited to allow for variables to be defensively allocated with generous sizes, by carefully ordering operations and checking operands in advance, it is often possible to ensure ''a priori'' that the result will never be larger than can be stored. Static analysis tools, formal verification and design by contract techniques can be used to more confidently and robustly ensure that an overflow cannot accidentally result.Handling
If it is anticipated that overflow may occur, then tests can be inserted into the program to detect when it happens, or is about to happen, and do other processing to mitigate it. For example, if an important result computed from user input overflows, the program can stop, reject the input, and perhaps prompt the user for different input, rather than the program proceeding with the invalid overflowed input and probably malfunctioning as a consequence. CPUs generally have a way to detect this to support addition of numbers larger than their register size, typically using a status bit. The technique is called multiple-precision arithmetic. Thus, it is possible to perform byte-wide addition on operands wider than a byte: first add the low bytes, store the result and check for overflow; then add the high bytes, and if necessary add the ''carry'' from the low bytes, then store the result. Handling possible overflow of a calculation may sometimes present a choice between performing a check ''before'' a calculation (to determine whether or not overflow is going to occur), or ''after'' it (to consider whether or not it likely occurred based on the resulting value). Since some implementations might generate a trap condition on integer overflow, the most portable programs test in advance of performing the operation that might overflow.Programming language support
Programming languages implement various mitigation methods against an accidental overflow: Ada, Seed7, and certain variants of functional languages trigger an exception condition on overflow, while Python (since 2.4) seamlessly converts internal representation of the number to match its growth, eventually representing it aslong – whose ability is only limited by the available memory.
In languages with native support for arbitrary-precision arithmetic and type safety (such as Python, Smalltalk
Smalltalk is a purely object oriented programming language (OOP) that was originally created in the 1970s for educational use, specifically for constructionist learning, but later found use in business. It was created at Xerox PARC by Learni ...
, or Common Lisp), numbers are promoted to a larger size automatically when overflows occur, or exceptions thrown (conditions signaled) when a range constraint exists. Using such languages may thus be helpful to mitigate this issue. However, in some such languages, situations are still possible where an integer overflow can occur. An example is explicit optimization of a code path which is considered a bottleneck by the profiler. In the case of Common Lisp, this is possible by using an explicit declaration to type-annotate a variable to a machine-size word (fixnum) and lower the type safety level to zero for a particular code block.
In stark contrast to older languages such as C, some newer languages such as Rust provide built-in functions that allow easy detection and user choice over how overflow should be handled case-by-case. In Rust, while use of basic mathematic operators naturally lacks such flexibility, users can alternatively perform calculations via a set of methods provided by each of the integer primitive types. These methods give users several choices between performing a ''checked'' (or ''overflowing'') operation (which indicates whether or not overflow occurred via the return type); an 'unchecked' operation; an operation that performs wrapping, or an operation which performs saturation at the numeric bounds.
Saturated arithmetic
Incomputer graphics
Computer graphics deals with generating images and art with the aid of computers. Computer graphics is a core technology in digital photography, film, video games, digital art, cell phone and computer displays, and many specialized applications. ...
or signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
, it is typical to work on data that ranges from 0 to 1 or from −1 to 1. For example, take a grayscale
In digital photography, computer-generated imagery, and colorimetry, a greyscale (more common in Commonwealth English) or grayscale (more common in American English) image is one in which the value of each pixel is a single sample (signal), s ...
image where 0 represents black, 1 represents white, and the values in between represent shades of gray. One operation that one may want to support is brightening the image by multiplying every pixel
In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a Raster graphics, raster image, or the smallest addressable element in a dot matrix display device. In most digital display devices, p ...
by a constant. Saturated arithmetic allows one to just blindly multiply every pixel by that constant without worrying about overflow by just sticking to a reasonable outcome that all these pixels larger than 1 (i.e., "brighter than white") just become white and all values "darker than black" just become black.
Examples
Unanticipated arithmetic overflow is a fairly common cause of program errors. Such overflow bugs may be hard to discover and diagnose because they may manifest themselves only for very large input data sets, which are less likely to be used in validation tests. Taking the arithmetic mean of two numbers by adding them and dividing by two, as done in many search algorithms, causes error if the sum (although not the resulting mean) is too large to be represented and hence overflows. Between 1985 and 1987, arithmetic overflow in the Therac-25radiation therapy
Radiation therapy or radiotherapy (RT, RTx, or XRT) is a therapy, treatment using ionizing radiation, generally provided as part of treatment of cancer, cancer therapy to either kill or control the growth of malignancy, malignant cell (biology), ...
machines, along with a lack of hardware safety controls, caused the death of at least six people from radiation overdoses.
An unhandled arithmetic overflow in the engine steering software was the primary cause of the crash of the 1996 maiden flight of the Ariane 5 rocket. The software had been considered bug-free since it had been used in many previous flights, but those used smaller rockets which generated lower acceleration than Ariane 5. Frustratingly, the part of the software in which the overflow error occurred was not even required to be running for the Ariane 5 at the time that it caused the rocket to fail: it was a launch-regime process for a smaller predecessor of the Ariane 5 that had remained in the software when it was adapted for the new rocket. Further, the true cause of the failure was a flaw in the engineering specification of how the software dealt with the overflow when it was detected: it did a diagnostic dump to its bus, which would have been connected to test equipment during software testing during development but was connected to the rocket steering motors during flight; the data dump drove the engine nozzle hard to one side which put the rocket out of aerodynamic control and precipitated its rapid breakup in the air.
On 30 April 2015, the U.S. Federal Aviation Administration
The Federal Aviation Administration (FAA) is a Federal government of the United States, U.S. federal government agency within the United States Department of Transportation, U.S. Department of Transportation that regulates civil aviation in t ...
announced it will order Boeing 787 operators to reset its electrical system periodically, to avoid an integer overflow which could lead to loss of electrical power and ram air turbine deployment, and Boeing deployed a software update in the fourth quarter. The European Aviation Safety Agency followed on 4 May 2015. The error happens after 231 hundredths of a second (about days), indicating a 32-bit signed integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
.
Overflow bugs are evident in some computer games. In '' Super Mario Bros.'' for the NES, the stored number of lives is a signed byte (ranging from −128 to 127) meaning the player can safely have 127 lives, but when the player reaches their 128th life, the counter rolls over to zero lives (although the number counter is glitched before this happens) and stops keeping count. As such, if the player then dies it's an immediate game over. This is caused by the game's data overflow that was an error of programming as the developers may not have thought said number of lives would be reasonably earned in a full playthrough.
In the arcade game '' Donkey Kong'', it is impossible to advance past level 22 due to an integer overflow in its time/bonus. The game calculates the time/bonus by taking the level number a user is on, multiplying it by 10, and adding 40. When they reach level 22, the time/bonus number is 260, which is too large for its 8-bit 256 value register, so it overflows to a value of 4 – too short to finish the level. In '' Donkey Kong Jr. Math'', when trying to calculate a number over 10,000, it shows only the first 4 digits. Overflow is the cause of the famous "split-screen" level in '' Pac-Man''. Such a bug also caused the ''Far Lands'' in ''Minecraft
''Minecraft'' is a 2011 sandbox game developed and published by the Swedish video game developer Mojang Studios. Originally created by Markus Persson, Markus "Notch" Persson using the Java (programming language), Java programming language, the ...
'' Java Edition which existed from the Infdev development period to Beta 1.7.3; it was later fixed in Beta 1.8. The same bug also existed in ''Minecraft'' Bedrock Edition but has since been fixed.
 IBM– Microsoft Macro Assembler (MASM) version 1.00, and likely all other programs built by the same Pascal compiler, had an integer overflow and signedness error in the stack setup code, which prevented them from running on newer DOS machines or emulators under some common configurations with more than 512 KiB of memory. The program either hangs or displays an error message and exits to DOS.
In August 2016, a
IBM– Microsoft Macro Assembler (MASM) version 1.00, and likely all other programs built by the same Pascal compiler, had an integer overflow and signedness error in the stack setup code, which prevented them from running on newer DOS machines or emulators under some common configurations with more than 512 KiB of memory. The program either hangs or displays an error message and exits to DOS.
In August 2016, a casino
A casino is a facility for gambling. Casinos are often built near or combined with hotels, resorts, restaurants, retail shops, cruise ships, and other tourist attractions. Some casinos also host live entertainment, such as stand-up comedy, conce ...
machine at Resorts World casino printed a prize ticket of $42,949,672.76 as a result of an overflow bug. The casino refused to pay this amount, calling it a malfunction, using in their defense that the machine clearly stated that the maximum payout was $10,000, so any prize exceeding that had to be the result of a programming bug. The New York State Gaming Commission ruled in favor of the casino.
See also
* Carry (arithmetic) *Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to mo ...
* Nuclear Gandhi
References
{{ReflistExternal links
Phrack #60, Basic Integer Overflows
* ttps://web.archive.org/web/20121010025025/http://www.cs.cmu.edu/~dbrumley/pubs/integer-ndss-07.pdf Efficient and Accurate Detection of Integer-based Attacksbr>WASC Threat Classification – Integer Overflows
Software bugs Computer security exploits Computer arithmetic de:Arithmetischer Überlauf