Archimedes's Use Of Infinitesimals

''The Method of Mechanical Theorems'' ( el, Περὶ μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένη ἔφοδος), also referred to as ''The Method'', is one of the major surviving works of the ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles (sometimes erroneously referred to as infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''.

Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises that contain the results. In these treatises, he proves the same theorems by exhaustion, finding rigorous upper and lower bounds which both converge to the answer required. Nevertheless, the mechanical method was what he used to discover the relations for which he later gave rigorous proofs.

Area of a parabola

To explain Archimedes' method today, it is convenient to make use of a little bit of Cartesian geometry, although this of course was unavailable at the time. His idea is to use the law of the lever to determine the areas of figures from the known center of mass of other figures. The simplest example in modern language is the area of the parabola. Archimedes uses a more elegant method, but in Cartesian language, his method is calculating the integral

$\int_0^1 x^2 \, dx = \frac,$

which can easily be checked nowadays using elementary integral calculus.

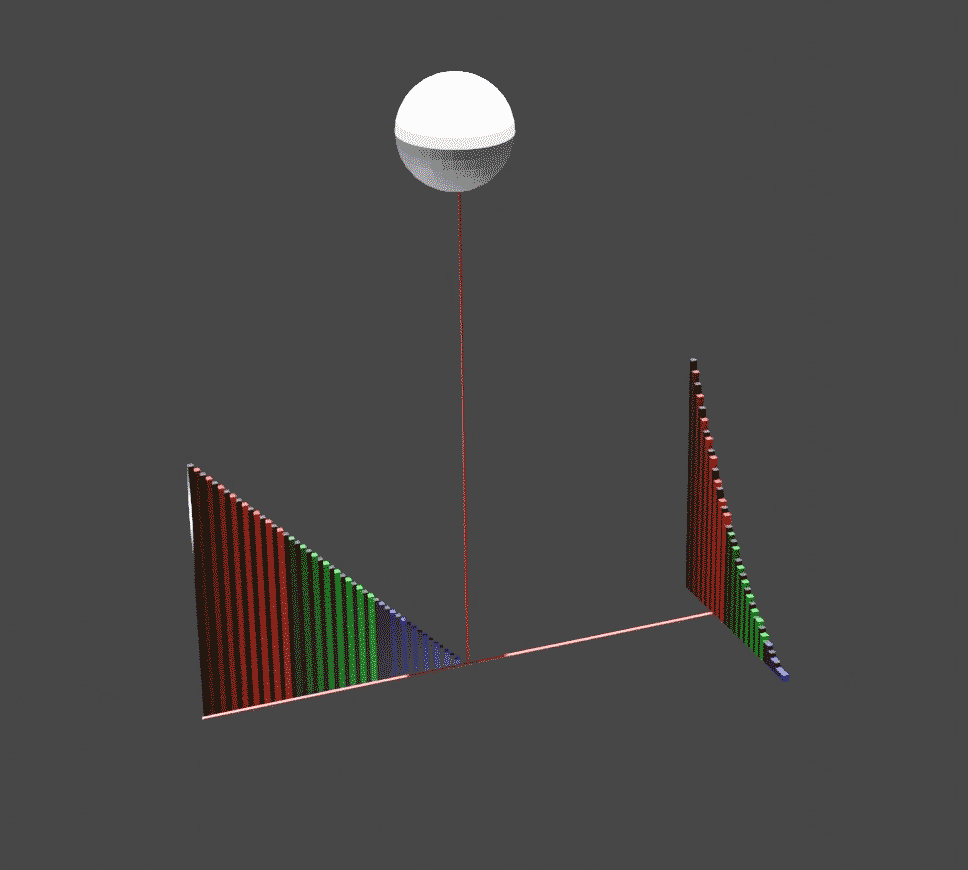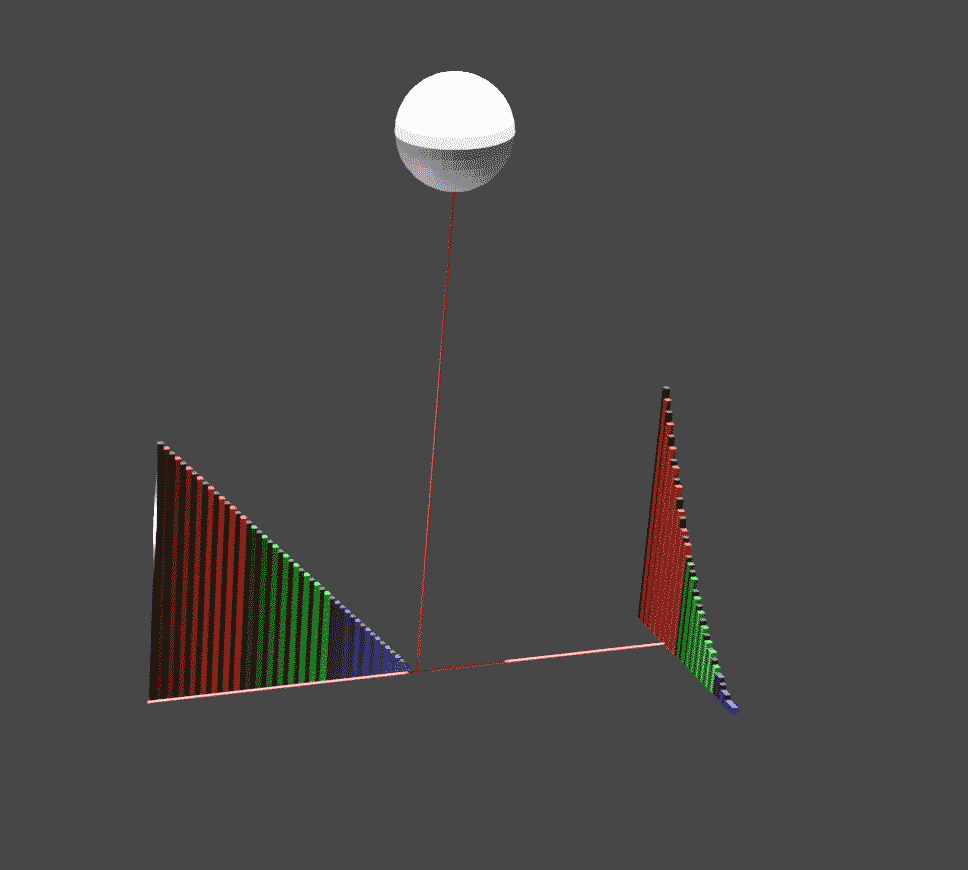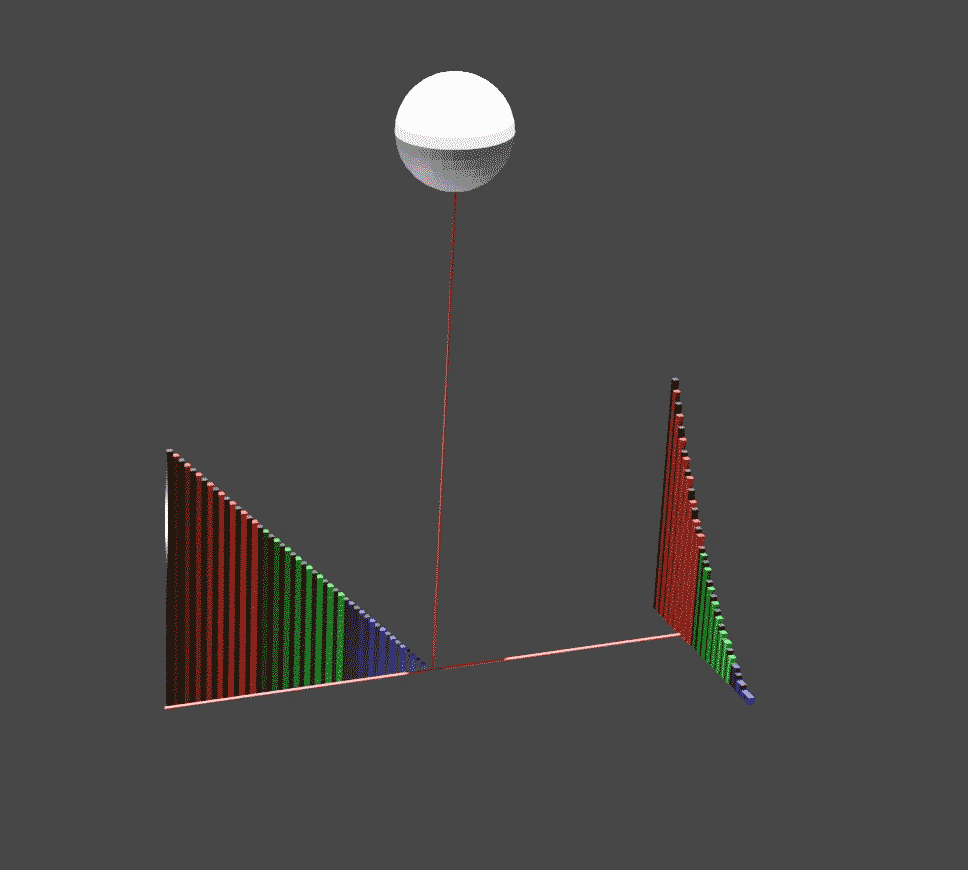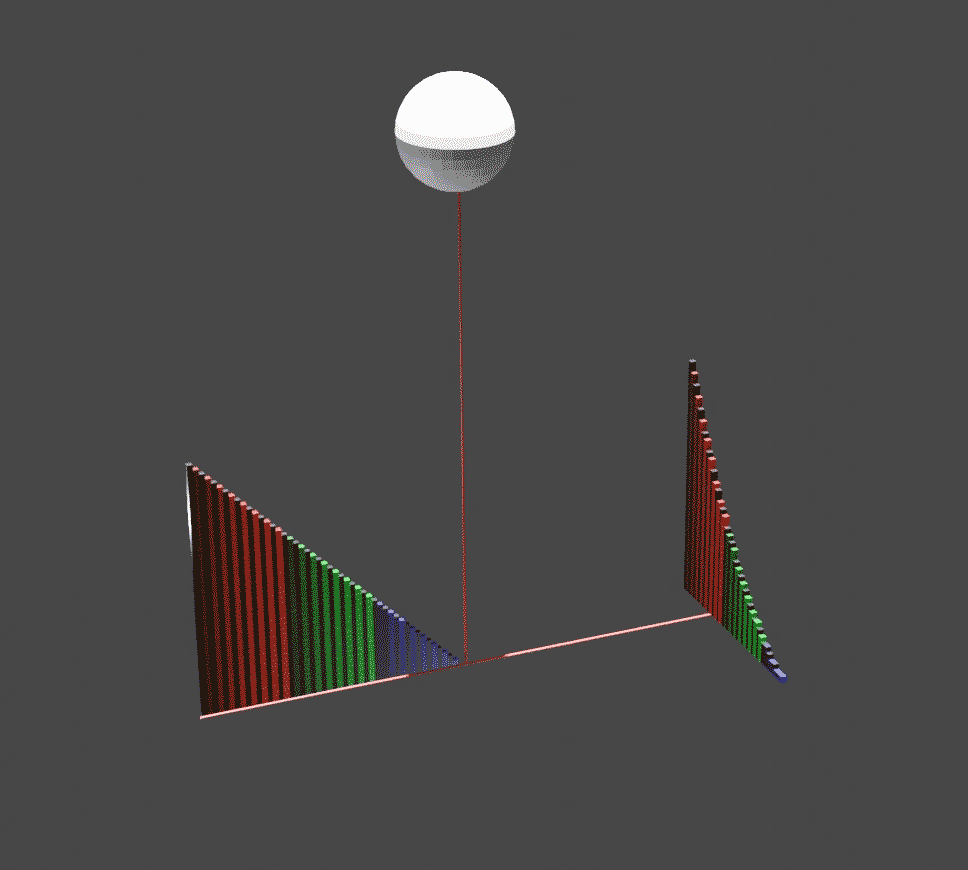
The idea is to mechanically balance the parabola (the curved region being integrated above) with a certain triangle that is made of the same material. The parabola is the region in the $(x,y)$ plane between the $x$-axis and the curve $y=x^2$ as $x$ varies from 0 to 1. The triangle is the region in the same plane between the $x$-axis and the line $y=x$, also as $x$ varies from 0 to 1.

Slice the parabola and triangle into vertical slices, one for each value of $x$. Imagine that the $x$-axis is a lever, with a fulcrum at $x=0$. The law of the lever states that two objects on opposite sides of the fulcrum will balance if each has the same torque, where an object's torque equals its weight times its distance to the fulcrum. For each value of $x$, the slice of the triangle at position $x$ has a mass equal to its height $x$, and is at a distance $x$ from the fulcrum; so it would balance the corresponding slice of the parabola, of height $x^2$, if the latter were moved to $x=-1$, at a distance of 1 on the other side of the fulcrum.

Since each pair of slices balances, moving the whole parabola to $x=-1$ would balance the whole triangle. This means that if the original uncut parabola is hung by a hook from the point $x=-1$ (so that the whole mass of the parabola is attached to that point), it will balance the triangle sitting between $x=0$ and $x=1$.

The center of mass of a triangle can be easily found by the following method, also due to Archimedes. If a median line is drawn from any one of the vertices of a triangle to the opposite edge $E$, the triangle will balance on the median, considered as a fulcrum. The reason is that if the triangle is divided into infinitesimal line segments parallel to $E$, each segment has equal length on opposite sides of the median, so balance follows by symmetry. This argument can be easily made rigorous by exhaustion by using little rectangles instead of infinitesimal lines, and this is what Archimedes does in ''On the Equilibrium of Planes''.

So the center of mass of a triangle must be at the intersection point of the medians. For the triangle in question, one median is the line $y=x/2$, while a second median is the line $y=1-x$. Solving these equations, we see that the intersection of these two medians is above the point $x=2/3$, so that the total effect of the triangle on the lever is as if the total mass of the triangle were pushing down on (or hanging from) this point. The total torque exerted by the triangle is its area, 1/2, times the distance 2/3 of its center of mass from the fulcrum at $x=0$. This torque of 1/3 balances the parabola, which is at a distance 1 from the fulcrum. Hence, the area of the parabola must be 1/3 to give it the opposite torque.

This type of method can be used to find the area of an arbitrary section of a parabola, and similar arguments can be used to find the integral of any power of $x$, although higher powers become complicated without algebra. Archimedes only went as far as the integral of $x^3$, which he used to find the center of mass of a hemisphere, and in other work, the center of mass of a parabola.

First proposition in the palimpsest

Consider the parabola in the figure to the right. Pick two points on the parabola and call them ''A'' and ''B''.

Suppose the line segment ''AC'' is parallel to the axis of symmetry of the parabola. Further suppose that the line segment ''BC'' lies on a line that is tangent to the parabola at ''B''.
The first proposition states:

:The area of the triangle ''ABC'' is exactly three times the area bounded by the parabola and the secant line ''AB''.

:''Proof'':
Let ''D'' be the midpoint of ''AC''. Construct a line segment ''JB'' through ''D'', where the distance from ''J'' to ''D'' is equal to the distance from ''B'' to ''D''. We will think of the segment ''JB'' as a "lever" with ''D'' as its fulcrum. As Archimedes had previously shown, the center of mass of the triangle is at the point ''I'' on the "lever" where ''DI'' :''DB'' = 1:3. Therefore, it suffices to show that if the whole weight of the interior of the triangle rests at ''I'', and the whole weight of the section of the parabola at ''J'', the lever is in equilibrium.

Consider an infinitely small cross-section of the triangle given by the segment ''HE'', where the point ''H'' lies on ''BC'', the point ''E'' lies on ''AB'', and ''HE'' is parallel to the axis of symmetry of the parabola. Call the intersection of ''HE'' and the parabola ''F'' and the intersection of ''HE'' and the lever ''G''. If the weight of all such segments ''HE'' rest at the points ''G'' where they intersect the lever, then they exert the same torque on the lever as does the whole weight of the triangle resting at ''I''. Thus, we wish to show that if the weight of the cross-section ''HE'' rests at ''G'' and the weight of the cross-section ''EF'' of the section of the parabola rests at ''J'', then the lever is in equilibrium. In other words, it suffices to show that ''EF'' :''GD'' = ''EH'' :''JD''. But that is a routine consequence of the equation of the parabola.  Q.E.D.

Volume of a sphere

Again, to illuminate the mechanical method, it is convenient to use a little bit of coordinate geometry. If a sphere of radius 1 is placed with its center at ''x'' = 1, the vertical cross sectional radius $\rho_S$ at any ''x'' between 0 and 2 is given by the following formula:
$\rho_S(x) = \sqrt.$

The mass of this cross section, for purposes of balancing on a lever, is proportional to the area:

$\pi \rho_S(x)^2 = 2\pi x - \pi x^2.$

Archimedes then considered rotating the triangular region between ''y'' = 0 and ''y'' = ''x'' and ''x'' = 2 on the ''x''-''y'' plane around the ''x''-axis, to form a cone. The cross section of this cone is a circle of radius $\rho_C$

$\rho_C(x) = x$

and the area of this cross section is

$\pi \rho_C^2 = \pi x^2.$

So if slices of the cone and the sphere ''both'' are to be weighed together, the combined cross-sectional area is:

$M(x) = 2\pi x.$

If the two slices are placed together at distance 1 from the fulcrum, their total weight would be exactly balanced by a circle of area $2\pi$ at a distance ''x'' from the fulcrum on the other side. This means that the cone and the sphere together, if all their material were moved to ''x'' = 1, would balance a cylinder of base radius 1 and length 2 on the other side.

As ''x'' ranges from 0 to 2, the cylinder will have a center of gravity a distance 1 from the fulcrum, so all the weight of the cylinder can be considered to be at position 1. The condition of balance ensures that the volume of the cone plus the volume of the sphere is equal to the volume of the cylinder.

The volume of the cylinder is the cross section area, $2\pi$ times the height, which is 2, or $4\pi$. Archimedes could also find the volume of the cone using the mechanical method, since, in modern terms, the integral involved is exactly the same as the one for area of the parabola. The volume of the cone is 1/3 its base area times the height. The base of the cone is a circle of radius 2, with area $4\pi$, while the height is 2, so the area is $8\pi/3$. Subtracting the volume of the cone from the volume of the cylinder gives the volume of the sphere:

$V_S = 4\pi - \pi = \pi.$

The dependence of the volume of the sphere on the radius is obvious from scaling, although that also was not trivial to make rigorous back then. The method then gives the familiar formula for the volume of a sphere. By scaling the dimensions linearly Archimedes easily extended the volume result to spheroids.

Archimedes argument is nearly identical to the argument above, but his cylinder had a bigger radius, so that the cone and the cylinder hung at a greater distance from the fulcrum. He considered this argument to be his greatest achievement, requesting that the accompanying figure of the balanced sphere, cone, and cylinder be engraved upon his tombstone.

Surface area of a sphere

To find the surface area of the sphere, Archimedes argued that just as the area of the circle could be thought of as infinitely many infinitesimal right triangles going around the circumference (see ''Measurement of the Circle''), the volume of the sphere could be thought of as divided into many cones with height equal to the radius and base on the surface. The cones all have the same height, so their volume is 1/3 the base area times the height.

Archimedes states that the total volume of the sphere is equal to the volume of a cone whose base has the same surface area as the sphere and whose height is the radius. There are no details given for the argument, but the obvious reason is that the cone can be divided into infinitesimal cones by splitting the base area up, and the each cone makes a contribution according to its base area, just the same as in the sphere.

Let the surface of the sphere be ''S''. The volume of the cone with base area ''S'' and height ''r'' is $Sr/3$, which must equal the volume of the sphere: $4\pi r^3/3$. Therefore, the surface area of the sphere must be $4\pi r^2$, or "four times its largest circle". Archimedes proves this rigorously in ''On the Sphere and Cylinder''.

Curvilinear shapes with rational volumes

One of the remarkable things about the ''Method'' is that Archimedes finds two shapes defined by sections of cylinders, whose volume does not involve $\pi$, despite the shapes having curvilinear boundaries. This is a central point of the investigation—certain curvilinear shapes could be rectified by ruler and compass, so that there are nontrivial rational relations between the volumes defined by the intersections of geometrical solids.

Archimedes emphasizes this in the beginning of the treatise, and invites the reader to try to reproduce the results by some other method. Unlike the other examples, the volume of these shapes is not rigorously computed in any of his other works. From fragments in the palimpsest, it appears that Archimedes did inscribe and circumscribe shapes to prove rigorous bounds for the volume, although the details have not been preserved.

The two shapes he considers are the intersection of two cylinders at right angles (the bicylinder), which is the region of (''x'', ''y'', ''z'') obeying:
$x^2 + y^2 <1, \quad y^2 + z^2 <1,$
and the circular prism, which is the region obeying:
x^2 + y^2<1, \quad 0
Both problems have a slicing which produces an easy integral for the mechanical method. For the circular prism, cut up the ''x''-axis into slices. The region in the ''y''-''z'' plane at any ''x'' is the interior of a right triangle of side length $\sqrt$ whose area is $(1-x^2)$, so that the total volume is:
$\displaystyle\int_^1 (1-x^2) \, dx$
which can be easily rectified using the mechanical method. Adding to each triangular section a section of a triangular pyramid with area $x^2/2$ balances a prism whose cross section is constant.

For the intersection of two cylinders, the slicing is lost in the manuscript, but it can be reconstructed in an obvious way in parallel to the rest of the document: if the x-z plane is the slice direction, the equations for the cylinder give that $x^2 < 1-y^2$ while $z^2 < 1-y^2$, which defines a region which is a square in the ''x''-''z'' plane of side length $2\sqrt$, so that the total volume is:
$\displaystyle\int_^1 4(1-y^2) \, dy.$
And this is the same integral as for the previous example. Jan Hogendijk argues that, besides the volume of the bicylinder, Archimedes knew its surface area, which is also rational.

Other propositions in the palimpsest

A series of propositions of geometry are proved in the palimpsest by similar arguments. One theorem is that the location of a center of mass of a hemisphere is located 5/8 of the way from the pole to the center of the sphere. This problem is notable, because it is evaluating a cubic integral.

See also

* Archimedes Palimpsest
* Method of indivisibles
* Method of exhaustion

References

{{DEFAULTSORT:Method of Mechanical Theorems
History of calculus
Archimedes
Works by Archimedes