620s BC Deaths on:
[Wikipedia]
[Google]
[Amazon]
6 (six) is the
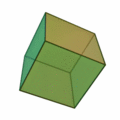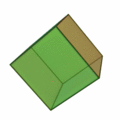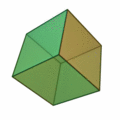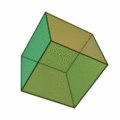 6 is the largest of the four
6 is the largest of the four
 ''Sex-'' is a
''Sex-'' is a

 The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the
The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the  .
This digit resembles an inverted ''9''. To disambiguate the two on objects and documents that can be inverted, the 6 has often been underlined, both in handwriting and on printed labels.
.
This digit resembles an inverted ''9''. To disambiguate the two on objects and documents that can be inverted, the 6 has often been underlined, both in handwriting and on printed labels.

 *In Judaism:
**Six points on a
*In Judaism:
**Six points on a
object
NGC 6, a spiral galaxy in the constellation Andromeda constellation, Andromeda *The Roman numeral VI: **Stands for subdwarfs in the stellar classification, Yerkes spectral classification scheme **(Usually) stands for the sixth-discovered satellite of a planet or minor planet (e.g. Jupiter VI) *6 Hebe
 *The cells of a beehive are hexagon, six-sided.
*Insects have six legs.
*Six kingdoms in the taxonomic rank below domain (biology); Animalia, Plantae, Fungi, Protista, Archaea/Archaeabacteria, and Bacteria/Eubacteria. See Kingdom (biology).
*The six elements most common in biomolecules are called the CHNOPS elements; the letters stand for the chemical abbreviations of carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur. See CHON.
*The cells of a beehive are hexagon, six-sided.
*Insects have six legs.
*Six kingdoms in the taxonomic rank below domain (biology); Animalia, Plantae, Fungi, Protista, Archaea/Archaeabacteria, and Bacteria/Eubacteria. See Kingdom (biology).
*The six elements most common in biomolecules are called the CHNOPS elements; the letters stand for the chemical abbreviations of carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur. See CHON.
 *A benzene molecule has a ring of six carbon atoms.
*6 is the atomic number of carbon.
*The sixfold symmetry of snowflakes arises from the
*A benzene molecule has a ring of six carbon atoms.
*6 is the atomic number of carbon.
*The sixfold symmetry of snowflakes arises from the
 *In the Standard Model of particle physics, there are six types of quarks and six types of leptons.
*In statistical mechanics, the Ice-type model, six-vertex model has six possible configurations of arrows at each vertex
*There are six colors in the RGB color wheel: (primary) red, blue, green, (secondary) cyan, magenta, and yellow. (See Tertiary color)
*In Three-dimensional space, three-dimensional Euclidean space, there are six unknown Reaction (physics), support reactions for a Statically indeterminate, statically determinate structure: one force in each of the three dimensions, and one moment (physics), moment through each of three possible orthogonal plane (geometry), planes.
*In the Standard Model of particle physics, there are six types of quarks and six types of leptons.
*In statistical mechanics, the Ice-type model, six-vertex model has six possible configurations of arrows at each vertex
*There are six colors in the RGB color wheel: (primary) red, blue, green, (secondary) cyan, magenta, and yellow. (See Tertiary color)
*In Three-dimensional space, three-dimensional Euclidean space, there are six unknown Reaction (physics), support reactions for a Statically indeterminate, statically determinate structure: one force in each of the three dimensions, and one moment (physics), moment through each of three possible orthogonal plane (geometry), planes.
 *On most phones, the 6 key is associated with the letters M, N, and O, but on the BlackBerry Pearl it is the key for J and K, and on the BlackBerry 8700 series and BlackBerry Curve 8900, Curve 8900 with full keyboard, it is the key for F
*The "6-meter band" in amateur radio includes the frequencies from 50 to 54 MHz
*6 is the resin identification code used in recycling to identify polystyrene
*On most phones, the 6 key is associated with the letters M, N, and O, but on the BlackBerry Pearl it is the key for J and K, and on the BlackBerry 8700 series and BlackBerry Curve 8900, Curve 8900 with full keyboard, it is the key for F
*The "6-meter band" in amateur radio includes the frequencies from 50 to 54 MHz
*6 is the resin identification code used in recycling to identify polystyrene
 *Six pack rings, Six pack is a common form of packaging for six bottles or cans of drink (especially beer), and by extension, other assemblages of six items.
*In Pythagorean numerology (a pseudoscience), the number 6 is the digit of balance, harmony and organization of the home and family
*The fundamental flight instruments lumped together on a cockpit display are often called the Basic Six or six-pack.
*The number of dots in a braille cell.
**See also Six degrees (disambiguation).
*Extrasensory perception is sometimes called the "sixth sense".
*Six Flags is an American company running amusement parks and theme parks in the U.S., Canada, and Mexico.
*In the U.S. Army "Six" as part of a Military call sign, radio call sign is used by the commanding officer of a unit, while subordinate platoon leaders usually go by "One".
(For a similar example see also: Rainbow Six (novel), Rainbow Six.)
*Six pack rings, Six pack is a common form of packaging for six bottles or cans of drink (especially beer), and by extension, other assemblages of six items.
*In Pythagorean numerology (a pseudoscience), the number 6 is the digit of balance, harmony and organization of the home and family
*The fundamental flight instruments lumped together on a cockpit display are often called the Basic Six or six-pack.
*The number of dots in a braille cell.
**See also Six degrees (disambiguation).
*Extrasensory perception is sometimes called the "sixth sense".
*Six Flags is an American company running amusement parks and theme parks in the U.S., Canada, and Mexico.
*In the U.S. Army "Six" as part of a Military call sign, radio call sign is used by the commanding officer of a unit, while subordinate platoon leaders usually go by "One".
(For a similar example see also: Rainbow Six (novel), Rainbow Six.)
The Number 6The Positive Integer 6
{{DEFAULTSORT:6 (Number) Integers 6 (number)
natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
following 5 and preceding 7. It is a composite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
and the smallest perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
.
In mathematics
Six is the smallest positive integer which is neither asquare number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
nor a prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
; it is the second smallest composite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
, behind 4; its proper divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
s are , and .
Since 6 equals the sum of its proper divisors, it is a perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
; 6 is the smallest of the perfect numbers. It is also the smallest Granville number In mathematics, specifically number theory, Granville numbers, also known as \mathcal-perfect numbers, are an extension of the perfect numbers.
The Granville set
In 1996, Andrew Granville proposed the following construction of a set \mathcal:
:Le ...
, or -perfect number.
As a perfect number:
*6 is related to the Mersenne prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17t ...
3, since . (The next perfect number is 28.)
*6 is the only even perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
that is not the sum of successive odd cubes.
*6 is the root of the 6-aliquot tree, and is itself the aliquot sum
In number theory, the aliquot sum ''s''(''n'') of a positive integer ''n'' is the sum of all proper divisors of ''n'', that is, all divisors of ''n'' other than ''n'' itself.
That is,
:s(n)=\sum\nolimits_d.
It can be used to characterize the prim ...
of only one other number; the square number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
, .
Six is the only number that is both the sum and the product of three consecutive positive numbers.
Unrelated to 6's being a perfect number, a Golomb ruler
In mathematics, a Golomb ruler is a set of marks at integer positions along a ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its ''order'', and the largest distance between two of its mar ...
of length 6 is a "perfect ruler". Six is a congruent number
In number theory, a congruent number is a positive integer that is the area of a right triangle with three rational number sides. A more general definition includes all positive rational numbers with this property.
The sequence of (integer) cong ...
.
Six is the first discrete biprime (2 × 3) and the first member of the (2 × ''q'') discrete biprime
In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers.
Because there are infinitely many prime n ...
family.
Six is a unitary perfect number
A unitary perfect number is an integer which is the sum of its positive proper unitary divisors, not including the number itself (a divisor ''d'' of a number ''n'' is a unitary divisor if ''d'' and ''n''/''d'' share no common factors). Some perfect ...
, a primary pseudoperfect number
In mathematics, and particularly in number theory, ''N'' is a primary pseudoperfect number if it satisfies the Egyptian fraction equation
:\frac + \sum_\frac = 1,
where the sum is over only the prime divisors of ''N''.
Properties
Equivalently, ...
, a harmonic divisor number
In mathematics, a harmonic divisor number, or Ore number (named after Øystein Ore who defined it in 1948), is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are:
: 1, 6, 2 ...
and a superior highly composite number
In mathematics, a superior highly composite number is a natural number which has the highest ratio of its number of divisors to ''some'' positive power of itself than any other number. It is a stronger restriction than that of a highly composite ...
, the last to also be a primorial
In mathematics, and more particularly in number theory, primorial, denoted by "#", is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function ...
.
There are no Graeco-Latin square
In combinatorics, two Latin squares of the same size (''order'') are said to be ''orthogonal'' if when superimposed the ordered paired entries in the positions are all distinct. A set of Latin squares, all of the same order, all pairs of which are ...
s with order 6. If ''n'' is a natural number that is not 2 or 6, then there is a Graeco-Latin square with order ''n''.
There is not a prime such that the multiplicative order of 2 modulo is 6, that is,
By Zsigmondy's theorem
In number theory, Zsigmondy's theorem, named after Karl Zsigmondy, states that if a>b>0 are coprime integers, then for any integer n \ge 1, there is a prime number ''p'' (called a ''primitive prime divisor'') that divides a^n-b^n and does not divi ...
, if is a natural number that is not 1 or 6, then there is a prime such that . See for such .
The ring of integer of the sixth cyclotomic field , which is called Eisenstein integer, has 6 units: ±1, ±ω, ±ω2, where .
The smallest non-abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commut ...
is the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \m ...
''S''3 which has 3! = 6 elements.
''S''6, with 720 = 6 ! elements, is the only finite symmetric group which has an outer automorphism In mathematics, the outer automorphism group of a group, , is the quotient, , where is the automorphism group of and ) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted . If is trivial and has a t ...
. This automorphism allows us to construct a number of exceptional mathematical objects such as the S(5,6,12) Steiner system
250px, thumbnail, The Fano plane is a Steiner triple system S(2,3,7). The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line.
In combinatorial mathematics, a Steiner system (named after Jakob Steiner) ...
, the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do ...
of order 4 and the Hoffman-Singleton graph. A closely related result is the following theorem: 6 is the only natural number ''n'' for which there is a construction of ''n'' isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
objects on an ''n''-set ''A'', invariant under all permutations of ''A'', but not naturally in one-to-one correspondence with the elements of ''A''. This can also be expressed category theoretically: consider the category
Category, plural categories, may refer to:
Philosophy and general uses
* Categorization, categories in cognitive science, information science and generally
*Category of being
* ''Categories'' (Aristotle)
*Category (Kant)
*Categories (Peirce)
* ...
whose objects are the ''n'' element sets and whose arrows are the bijection
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other s ...
s between the sets. This category has a non-trivial functor
In mathematics, specifically category theory, a functor is a Map (mathematics), mapping between Category (mathematics), categories. Functors were first considered in algebraic topology, where algebraic objects (such as the fundamental group) ar ...
to itself only for .
Six similar coins can be arranged around a central coin of the same radius so that each coin makes contact with the central one (and touches both its neighbors without a gap), but seven cannot be so arranged. This makes 6 the answer to the two-dimensional kissing number problem
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement of ...
. The densest sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing p ...
of the plane is obtained by extending this pattern to the hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°.
Regular hexa ...
al lattice
Lattice may refer to:
Arts and design
* Latticework, an ornamental criss-crossed framework, an arrangement of crossing laths or other thin strips of material
* Lattice (music), an organized grid model of pitch ratios
* Lattice (pastry), an orna ...
in which each circle touches just six others.
 6 is the largest of the four
6 is the largest of the four all-Harshad number
In mathematics, a harshad number (or Niven number) in a given number base is an integer that is divisible by the sum of its digits when written in that base.
Harshad numbers in base are also known as -harshad (or -Niven) numbers.
Harshad number ...
s.
A six-sided polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two toge ...
is a hexagon, one of the three regular polygons capable of tiling the plane. Figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean
* polygon ...
s representing hexagons (including six) are called hexagonal number
A hexagonal number is a figurate number. The ''n''th hexagonal number ''h'n'' is the number of ''distinct'' dots in a pattern of dots consisting of the ''outlines'' of regular hexagons with sides up to n dots, when the hexagons are overlaid so ...
s. Because 6 is the product of a power of 2 (namely 21) with nothing but distinct Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
s (specifically 3), a regular hexagon is a constructible polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinite ...
.
Six is also an octahedral number
In number theory, an octahedral number is a figurate number that represents the number of spheres in an octahedron formed from close-packed spheres. The ''n''th octahedral number O_n can be obtained by the formula:.
:O_n=.
The first few octahed ...
. It is a triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
and so is its square ().
There are six basic trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
.
There are six convex regular polytopes in four dimensions
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordina ...
.
The six exponentials theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials.
Statement
If ''x''1, '' ...
guarantees (given the right conditions on the exponents) the transcendence of at least one of a set of exponentials.
All primes above 3 are of the form 6''n'' ± 1 for ''n'' ≥ 1.
6 is a pronic number A pronic number is a number that is the product of two consecutive integers, that is, a number of the form n(n+1).. The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers,. or rectangular number ...
and the only semiprime to be.
There are six different ways in which 100 can be expressed as the sum of two prime numbers -- 3 + 97, 11 + 89, 17 + 83, 29 + 71, 41 + 59 and 47 + 53.
List of basic calculations
Greek and Latin word parts
'
' is classicalGreek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
for "six". Thus:
*"Hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, hexa ...
" combines ' with the Latinate ' to name a number base
In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal/denary system (the most common system in use today) the radix (base number) is t ...
of 16
*A hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°.
Regular hexa ...
is a regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
with six sides
**' is a French nickname for the continental part of Metropolitan France
Metropolitan France (french: France métropolitaine or ''la Métropole''), also known as European France (french: Territoire européen de la France) is the area of France which is geographically in Europe. This collective name for the European ...
for its resemblance to a regular hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A '' regular hexagon'' has ...
*A hexahedron
A hexahedron (plural: hexahedra or hexahedrons) or sexahedron (plural: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.
There ...
is a polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on th ...
with six faces, with a cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
being a special case
*Hexameter
Hexameter is a metrical line of verses consisting of six feet (a "foot" here is the pulse, or major accent, of words in an English line of poetry; in Greek and Latin a "foot" is not an accent, but describes various combinations of syllables). It w ...
is a poetic form consisting of six feet per line
*A "hex nut" is a nut
Nut often refers to:
* Nut (fruit), fruit composed of a hard shell and a seed, or a collective noun for dry and edible fruits or seeds
* Nut (hardware), fastener used with a bolt
Nut or Nuts may also refer to:
Arts, entertainment, and media Co ...
with six sides, and a hex bolt has a six-sided head
*The prefix "" also occurs in the systematic name A systematic name is a name given in a systematic way to one unique group, organism, object or chemical substance, out of a specific population or collection. Systematic names are usually part of a nomenclature.
A semisystematic name or semitrivial ...
of many chemical compound
A chemical compound is a chemical substance composed of many identical molecules (or molecular entities) containing atoms from more than one chemical element held together by chemical bonds. A molecule consisting of atoms of only one element ...
s, such as hexane
Hexane () is an organic compound, a straight-chain alkane with six carbon atoms and has the molecular formula C6H14.
It is a colorless liquid, odorless when pure, and with boiling points approximately . It is widely used as a cheap, relatively ...
which has 6 carbon atoms ().
The prefix ''sex-''
 ''Sex-'' is a
''Sex-'' is a Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the ...
prefix
A prefix is an affix which is placed before the Word stem, stem of a word. Adding it to the beginning of one word changes it into another word. For example, when the prefix ''un-'' is added to the word ''happy'', it creates the word ''unhappy'' ...
meaning "six". Thus:
*''Senary'' is the ordinal adjective meaning "sixth"
*People with sexdactyly have six fingers on each hand
*The measuring instrument called a sextant
A sextant is a doubly reflecting navigation instrument that measures the angular distance between two visible objects. The primary use of a sextant is to measure the angle between an astronomical object and the horizon for the purposes of celes ...
got its name because its shape forms one-sixth of a whole circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
*A group of six musicians is called a sextet
A sextet (or hexad) is a formation containing exactly six members. The former term is commonly associated with vocal ensembles (e.g. The King's Singers, Affabre Concinui) or musical instrument groups, but can be applied to any situation where six ...
*Six babies delivered in one birth are sextuplet
A multiple birth is the culmination of one multiple pregnancy, wherein the mother gives birth to two or more babies. A term most applicable to vertebrate species, multiple births occur in most kinds of mammals, with varying frequencies. Such bi ...
s
*Sexy prime
In number theory, sexy primes are prime numbers that differ from each other by 6. For example, the numbers 5 and 11 are both sexy primes, because both are prime and .
The term "sexy prime" is a pun stemming from the Latin word for six: .
If o ...
pairs – Prime pairs differing by six are ''sexy'', because sex is the Latin word for six.
The SI prefix
The International System of Units, known by the international abbreviation SI in all languages and sometimes pleonastically as the SI system, is the modern form of the metric system and the world's most widely used system of measurement. E ...
for 10006 is exa-
A metric prefix is a unit prefix that precedes a basic unit of measure to indicate a multiple or submultiple of the unit. All metric prefixes used today are decadic. Each prefix has a unique symbol that is prepended to any unit symbol. The pre ...
(E), and for its reciprocal atto-
A metric prefix is a unit prefix that precedes a basic unit of measure to indicate a multiple or submultiple of the unit. All metric prefixes used today are decadic. Each prefix has a unique symbol that is prepended to any unit symbol. The pre ...
(a).
Evolution of the Arabic digit

 The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the
The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the Brahmi numerals
The Brahmi numerals are a numeral system attested from the 3rd century BCE (somewhat later in the case of most of the tens). They are a non positional decimal system. They are the direct graphic ancestors of the modern Hindu–Arabic numeral s ...
of India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the so ...
, which are first known from the Edicts of Ashoka
The Edicts of Ashoka are a collection of more than thirty inscriptions on the Pillars of Ashoka, as well as boulders and cave walls, attributed to Emperor Ashoka of the Maurya Empire who reigned from 268 BCE to 232 BCE. Ashoka used the expres ...
circa 250 BCE. It was written in one stroke like a cursive lowercase e rotated 90 degrees clockwise. Gradually, the upper part of the stroke (above the central squiggle) became more curved, while the lower part of the stroke (below the central squiggle) became straighter. The Arabs dropped the part of the stroke below the squiggle. From there, the European evolution to our modern 6 was very straightforward, aside from a flirtation with a glyph that looked more like an uppercase G.
On the seven-segment display
A seven-segment display is a form of electronic display device for displaying decimal numerals that is an alternative to the more complex dot matrix displays.
Seven-segment displays are widely used in digital clocks, electronic meters, basic ...
s of calculators and watches, 6 is usually written with six segments. Some historical calculator models use just five segments for the 6, by omitting the top horizontal bar. This glyph variant has not caught on; for calculators that can display results in hexadecimal, a 6 that looks like a "b" is not practical.
Just as in most modern typeface
A typeface (or font family) is the design of lettering that can include variations in size, weight (e.g. bold), slope (e.g. italic), width (e.g. condensed), and so on. Each of these variations of the typeface is a font.
There are list of type ...
s, in typefaces with text figures
Text figures (also known as non-lining, lowercase, old style, ranging, hanging, medieval, billing, or antique figures or numerals) are numerals designed with varying heights in a fashion that resembles a typical line of running text, hence the ...
the character for the digit 6 usually has an ascender, as, for example, in In music

In artists
*' ("The Six" in English) was a group consisting of the French composers , , , , and in the 1920s * Bands with the number six in their name includeSix Organs of Admittance
Six Organs of Admittance is the primary musical project of American guitarist Ben Chasny. Chasny's music is largely guitar-based and is often considered new folk; however, it includes obvious influences, marked by the use of drones, chimes, and ...
, 6 O'Clock Saints, Electric Six
Electric Six is a six-piece American rock band formed in 1996 in Detroit, Michigan. Their music was described by AllMusic as a combination of garage, disco, punk rock, new wave, and metal. The band achieved recognition in 2003 with the singl ...
, Eve 6
Eve 6 is an American rock band formed in 1995 in Southern California, best known for their hit singles " Inside Out," "Leech," " Here's to the Night," and "Promise." They disbanded in 2004, returned for numerous tours in 2007 with a new lineup ...
, Los Xey
LOS, or Los, or LoS may refer to:
Science and technology
* Length of stay, the duration of a single episode of hospitalisation
* Level of service, a measure used by traffic engineers
* Level of significance, a measure of statistical significan ...
(' is Basque for "six"), Out On Blue Six, Six In Six, Sixpence None the Richer
Sixpence None the Richer (also known as Sixpence) is an American Christian alternative rock band that formed in New Braunfels, Texas, and eventually settled in Nashville, Tennessee. They are best known for their songs " Kiss Me" and " Breathe Yo ...
, Slant 6
Slant 6 was an American punk rock trio based in Washington, D.C. affiliated with early riot grrrl.
Slant 6 consisted of Christina Billotte (electric guitar and vocals), Myra Power (electric bass guitar and vocals), and Marge Marshall (drum se ...
, Vanity 6, and You Me At Six
You Me at Six are an English rock band from Weybridge, Surrey. The band consists of lead singer Josh Franceschi, guitarists Max Helyer and Chris Miller, bassist Matt Barnes and drummer Daniel Flint. Formed in 2004, the name for the group origin ...
* #6 is the pseudonym of American
American(s) may refer to:
* American, something of, from, or related to the United States of America, commonly known as the "United States" or "America"
** Americans, citizens and nationals of the United States of America
** American ancestry, pe ...
musician Shawn Crahan
Michael Shawn Crahan (born September 24, 1969), more commonly known by his stage persona "Clown", is an American musician. He is the co-founder and one of two percussionists for heavy metal band Slipknot in which he is designated #6. Crahan he ...
, when performing with the band Slipknot
In instruments
*A standardguitar
The guitar is a fretted musical instrument that typically has six strings. It is usually held flat against the player's body and played by strumming or plucking the strings with the dominant hand, while simultaneously pressing selected stri ...
has six strings
*Most woodwind
Woodwind instruments are a family of musical instruments within the greater category of wind instruments. Common examples include flute, clarinet, oboe, bassoon, and saxophone. There are two main types of woodwind instruments: flutes and reed ...
instruments have six basic holes or keys (e.g., bassoon, clarinet, pennywhistle, saxophone); these holes or keys are usually not given numbers or letters in the fingering charts
In music theory
*There are six whole tones in an octave. *There are six semitones in a tritone.In works
*"Six geese a-laying" were given as a present on the sixth day in the popularChristmas carol
A Christmas carol is a carol (a song or hymn) on the theme of Christmas, traditionally sung at Christmas itself or during the surrounding Christmas holiday season. The term noel has sometimes been used, especially for carols of French ori ...
, "The Twelve Days of Christmas
The Twelve Days of Christmas, also known as Twelvetide, is a festive Christian season celebrating the Nativity of Jesus. In some Western ecclesiastical traditions, "Christmas Day" is considered the "First Day of Christmas" and the Twelve Days a ...
."
*Divided in six arias, ''Hexachordum Apollinis
''Hexachordum Apollinis'' (PWC 193–8, T. 211–6, PC 131–6, POP 1–6) is a collection of keyboard music by Johann Pachelbel, published in 1699. It comprises six arias with variations, on original themes, and is generally regarded as one of th ...
'' is generally regarded as one of the pinnacles of Johann Pachelbel
Johann Pachelbel (baptised – buried 9 March 1706; also Bachelbel) was a German composer, organist, and teacher who brought the south German organ schools to their peak. He composed a large body of sacred and secularity, secular music, and h ...
's oeuvre.
*The theme of the sixth album by Dream Theater, ''Six Degrees of Inner Turbulence
''Six Degrees of Inner Turbulence'' is the sixth full-length studio album by progressive metal band Dream Theater, released as a double-disc album on January 29, 2002 through Elektra Records. Excluding the ''A Change of Seasons'' EP, it is the ...
'', was the number six: the album has six songs, and the sixth song — that is, the complete second disc — explores the stories of six individuals suffering from various mental illnesses.
*Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
gave six elements of tragedy, the first of which is Mythos
Myth is a folklore genre consisting of narratives that play a fundamental role in a society, such as foundational tales or origin myths. Since "myth" is widely used to imply that a story is not objectively true, the identification of a narrati ...
.
In religion
Star of David
The Star of David (). is a generally recognized symbol of both Jewish identity and Judaism. Its shape is that of a hexagram: the compound of two equilateral triangles.
A derivation of the ''seal of Solomon'', which was used for decorative ...
**Six orders of the Mishnah
The Mishnah or the Mishna (; he, מִשְׁנָה, "study by repetition", from the verb ''shanah'' , or "to study and review", also "secondary") is the first major written collection of the Jewish oral traditions which is known as the Oral Torah ...
**Six symbolic foods placed on the Passover Seder Plate
The Passover Seder plate ( he, קערה, ''ke'ara'') is a special plate containing symbolic foods eaten or displayed at the Passover Seder. The purpose of the Passover Seder plate is to show all the foods that perpetuate and emphasize the ideas ...
**God took six days to create the world in the Old Testament Book of Genesis; humankind was created on day 6. In the City of God (book), ''City of God'', Augustine of Hippo suggested (book 11, chapter 30) that God's creation of the world took six days because 6 is a perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
.
**The Judaism, Jewish holiday of Shavuot starts on the sixth day of the Hebrew calendar, Hebrew month of Sivan
**Seraphs have six wings.
*In Islam:
**There are Six articles of belief
**Fasting six days of Shawwal, together with the month of Ramadan, is equivalent to fasting the whole year
*In Āstika and nāstika, Hindu theology, a ''Hindu units of measurement#Small units of time used in the Vedas, trasarenu'' is the combination of six celestial (Vaisheshika#The atomic theory, atoms).
*In Taoism:
**Six Lines of a I Ching, Hexagram
**Three Departments and Six Ministries, Six Ministries of Emperor of China, Huang Di
In science
Astronomy
*Messier object Messier Object 6, M6, a magnitude 4.5 open cluster in the constellation Scorpius, also known as the Butterfly Cluster *The New General Catalogue]object
NGC 6, a spiral galaxy in the constellation Andromeda constellation, Andromeda *The Roman numeral VI: **Stands for subdwarfs in the stellar classification, Yerkes spectral classification scheme **(Usually) stands for the sixth-discovered satellite of a planet or minor planet (e.g. Jupiter VI) *6 Hebe
Biology
 *The cells of a beehive are hexagon, six-sided.
*Insects have six legs.
*Six kingdoms in the taxonomic rank below domain (biology); Animalia, Plantae, Fungi, Protista, Archaea/Archaeabacteria, and Bacteria/Eubacteria. See Kingdom (biology).
*The six elements most common in biomolecules are called the CHNOPS elements; the letters stand for the chemical abbreviations of carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur. See CHON.
*The cells of a beehive are hexagon, six-sided.
*Insects have six legs.
*Six kingdoms in the taxonomic rank below domain (biology); Animalia, Plantae, Fungi, Protista, Archaea/Archaeabacteria, and Bacteria/Eubacteria. See Kingdom (biology).
*The six elements most common in biomolecules are called the CHNOPS elements; the letters stand for the chemical abbreviations of carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur. See CHON.
Chemistry
 *A benzene molecule has a ring of six carbon atoms.
*6 is the atomic number of carbon.
*The sixfold symmetry of snowflakes arises from the
*A benzene molecule has a ring of six carbon atoms.
*6 is the atomic number of carbon.
*The sixfold symmetry of snowflakes arises from the hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°.
Regular hexa ...
al crystal structure of Ice, ordinary ice.
*A hexamer is an oligomer made of six subunits.
Medicine
*There are six tastes in traditional Indian medicine (Ayurveda): sweet, sour, salty, bitter, pungent, and astringent. These tastes are used to suggest a diet based on the symptoms of the body. *Phase 6 is one of six WHO pandemic phases, pandemic influenza phases.Physics
In sports
* The Original Six teams in the National Hockey League are Toronto Maple Leafs, Toronto, Chicago Blackhawks, Chicago, Montreal Canadiens, Montreal, New York Rangers, New York, Boston Bruins, Boston, and Detroit Red Wings, Detroit. They are the oldest remaining teams in the league, though not necessarily the first six; they comprised the entire league from 1942–43 NHL season, 1942 to 1967 NHL expansion, 1967. * Number of players: ** In association football (soccer), the number of substitutes combined by both teams, that are allowed in the game. ** In box lacrosse, the number of players per team, including the goaltender, that are on the floor at any one time, excluding penalty situations. ** In ice hockey, the number of players per team, including the goaltender, that are on the ice at any one time during regulation play, excluding penalty situations. (Some leagues reduce the number of players on the ice during overtime.) ** In volleyball: *** Six players from each team on each side play against each other. *** Standard rules only allow six total substitutions per team per set. (Substitutions involving the libero, a defensive specialist who can only play in the back row, are not counted against this limit.) ** Six-man football is a variant of American or Canadian football, played by smaller schools with insufficient enrollment to field the traditional 11-man (American) or 12-man (Canadian) squad. * Scoring: ** In both American football, American and Canadian football, 6 points are awarded for a touchdown. ** In Australian rules football, 6 points are awarded for a goal, scored when a kicked ball passes between the defending team's two inner goalposts without having been touched by another player. ** In cricket, six runs are scored for the batting team when the ball is hit to the boundary or the ground beyond it without having touched the ground in the field. * In basketball, the Basketball (ball), ball used for women's full-court competitions is designated "size 6". * In most rugby league competitions (but not the Super League, which uses static squad numbering), the jersey number 6 is worn by the starting (Southern Hemisphere term) or (Northern Hemisphere term). * In rugby union, the starting blindside flanker wears jersey number 6. (Some teams use "left" and "right" flankers instead of "openside" and "blindside", with 6 being worn by the starting left flanker.)In technology
In calendars
*In the ancient Roman calendar, Sextilis was the sixth month. After the Julian calendar, Julian reform, June became the sixth month and Sextilis was renamed August *Sextidi was the sixth day of the ''wikt:décade, décade'' in the French Revolutionary calendarIn the arts and entertainment
Games
*The number of sides on a cube, hence the highest number on a standard dice, die *The six-sided tiles on a hex grid are used in many tabletop and board games. *The highest number on one end of a standard Dominoes, dominoComics and cartoons
*''The Super 6'', a 1966 animated cartoon series featuring six different super-powered heroes.Literature
*''The Power of Six'' is a book written by Pittacus Lore, and the second in the Lorien Legacies series. *Number 6 is a character in the book series Lorien LegaciesTV
* Number Six (Battlestar Galactica), Number Six (Tricia Helfer), is a family of fictional characters from the reimagined science fiction television series, ''Battlestar Galactica (2004 TV series), Battlestar Galactica'' *Number 6, the main protagonist in ''The Prisoner'' played by Patrick McGoohan, and portrayed by Jim Caviezel in The Prisoner (2009 miniseries), the remake. *Six is a character in the television series ''Blossom (TV series), Blossom'' played by Jenna von Oÿ. *Six is the nickname of Kal Varrik, a central character in the television series ''Dark Matter (TV Series), Dark Matter'', played by Roger Cross. *''Six (TV series), Six'' is a History (U.S. TV channel), History channel series that chronicles the operations and daily lives of SEAL Team Six. *''Six Feet Under (TV series), Six Feet Under'', an HBO series that ran from 2005 to 2011.Movies
*Number 6 (Teresa Palmer) is a character in the movie ''I Am Number Four (film), I Am Number Four'' (2011). *''The 6th Day'' (2000), starring Arnold Schwarzenegger. *''The Sixth Sense'' (1999), written and directed by M. Night Shyamalan and starring Haley Joel Osment and Bruce Willis. *''Girl 6'' (1996), directed by Spike Lee.Musicals
* Six (musical), ''Six'' is a modern retelling of the lives of the six wives of Henry VIII presented as a pop concert.Anthropology
*The name of the smallest group of Cub Scouts and Guiding's equivalent Brownie (Girl Guides), Brownies, traditionally consisting of six people and is led by a "sixer". *A coffin is traditionally buried six feet under the ground; thus, the phrase "six feet under" means that a person (or thing, or concept) is dead *There are said to be no more than six degrees of separation between any two people on Earth. *In Western astrology, Virgo (astrology), Virgo is the 6th astrological sign of the Zodiac *The Six Dynasties form part of Chinese history *Six is a lucky numbers in Chinese culture, number in Chinese culture. *The Birmingham Six were a British miscarriage of justice, held in prison for 16 years. *"Six" is used as an informal slang term for the British Secret Intelligence Service, MI6.In other fields
See also
*List of highways numbered 6References
*''The Odd Number 6'', JA Todd, Math. Proc. Camb. Phil. Soc. 41 (1945) 66–68 *''A Property of the Number Six'', Chapter 6, P Cameron, JH v. Lint, ''Designs, Graphs, Codes and their Links'' *Wells, D. ''The Penguin Dictionary of Curious and Interesting Numbers'' London: Penguin Group. (1987): 67 - 69External links
The Number 6
{{DEFAULTSORT:6 (Number) Integers 6 (number)