4-cube T3 A3 on:
[Wikipedia]
[Google]
[Amazon]

 In
In
 The construction of
The construction of  The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts ( 16-cells). It can also be triangulated into 4-dimensional
The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts ( 16-cells). It can also be triangulated into 4-dimensional

 The ''cell-first'' parallel
The ''cell-first'' parallel 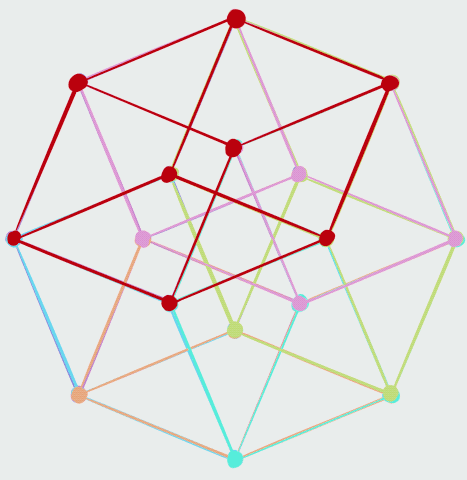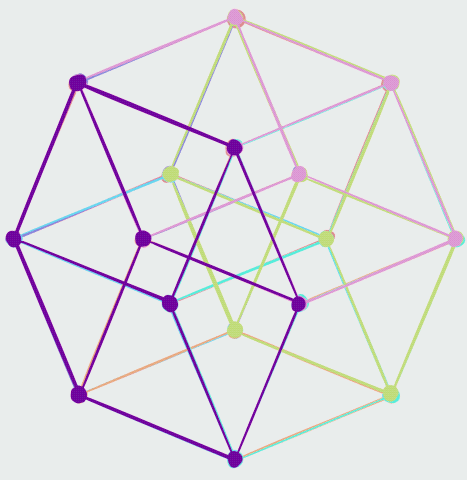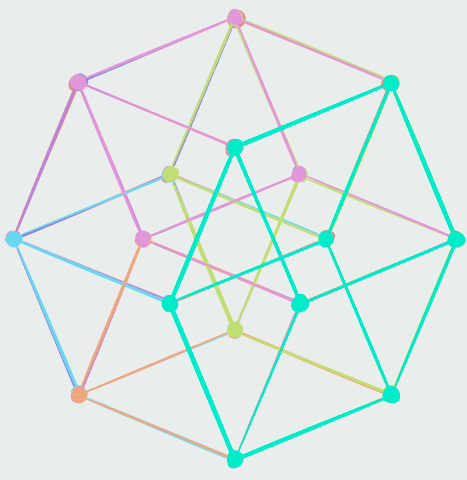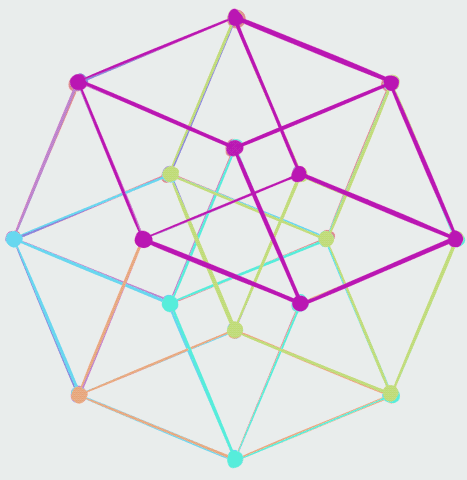
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'',
"The projection of fourfold figures on a three-flat"
The Tesseract
Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
Marco Möller's Regular polytopes in ℝ4 (German)
WikiChoron: Tesseract
is an open source program for the
Hypercube 98
A
ken perlin's home page
A way to visualize hypercubes, by
Some Notes on the Fourth Dimension
includes animated tutorials on several different aspects of the tesseract, b
Davide P. Cervone
{{Polytopes Algebraic topology Four-dimensional geometry 008

 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a tesseract is the four-dimensional
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
analogue of the cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
; the tesseract is to the cube as the cube is to the square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
. Just as the surface of the cube consists of six square faces
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affe ...
, the hypersurface
In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidean ...
of the tesseract consists of eight cubical cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
. The tesseract is one of the six convex regular 4-polytope
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six convex and ten star regu ...
s.
The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s or measure polytopes. Coxeter labels it the polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
.
The ''Oxford English Dictionary
The ''Oxford English Dictionary'' (''OED'') is the first and foundational historical dictionary of the English language, published by Oxford University Press (OUP). It traces the historical development of the English language, providing a com ...
'' traces the word ''tesseract'' to Charles Howard Hinton
Charles Howard Hinton (1853 – 30 April 1907) was a British mathematician and writer of science fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imaginative and ...
's 1888 book ''A New Era of Thought
''A New Era of Thought'' is a non-fiction work written by Charles Howard Hinton, published in 1888 and reprinted in 1900 by Swan Sonnenschein & Co. Ltd., London. ''A New Era of Thought'' is about the fourth dimension and its implications on human ...
''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled the word as ''tessaract''.
Geometry
As aregular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or -faces (for all , where is the dimension of the polytope) — cells, f ...
with three cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
s folded together around every edge, it has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
with hyperoctahedral symmetry of order 384. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol × , with symmetry order 96. As a 4-4 duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
, a Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ti ...
of two squares
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
, it can be named by a composite Schläfli symbol ×, with symmetry order 64. As an orthotope
In geometry, an orthotopeCoxeter, 1973 (also called a hyperrectangle or a box) is the generalization of a rectangle to higher dimensions.
A necessary and sufficient condition is that it is Congruence (geometry), congruent to the Cartesian product ...
it can be represented by composite Schläfli symbol × × × or 4, with symmetry order 16.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
of the tesseract is a regular tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
. The dual polytope
In geometry, every polyhedron is associated with a second dual structure, where the Vertex (geometry), vertices of one correspond to the Face (geometry), faces of the other, and the edges between pairs of vertices of one correspond to the edges b ...
of the tesseract is the 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
with Schläfli symbol , with which it can be combined to form the compound of tesseract and 16-cell
In 4-dimensional geometry, the tesseract 16-cell compound is a polytope compound composed of a regular tesseract and its dual, the regular 16-cell. Its convex hull is the regular 24-cell, which is self-dual.
A '' compound polytope'' is a figure t ...
.
Each edge of a regular tesseract is of the same length. This is of interest when using tesseracts as the basis for a network topology
Network topology is the arrangement of the elements ( links, nodes, etc.) of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, including command and contro ...
to link multiple processors in parallel computing
Parallel computing is a type of computation in which many calculations or processes are carried out simultaneously. Large problems can often be divided into smaller ones, which can then be solved at the same time. There are several different fo ...
: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Coordinates
The standard tesseract in Euclidean 4-space is given as theconvex hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space ...
of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
:
In this Cartesian frame of reference, the tesseract has radius 2 and is bounded by eight hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
s (''x''i = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Net
An unfolding of apolytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
is called a net
Net or net may refer to:
Mathematics and physics
* Net (mathematics), a filter-like topological generalization of a sequence
* Net, a linear system of divisors of dimension 2
* Net (polyhedron), an arrangement of polygons that can be folded up ...
. There are 261 distinct nets of the tesseract. The unfoldings of the tesseract can be counted by mapping the nets to ''paired trees'' (a tree
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, including only woody plants with secondary growth, plants that are ...
together with a perfect matching
In graph theory, a perfect matching in a graph is a matching that covers every vertex of the graph. More formally, given a graph , a perfect matching in is a subset of edge set , such that every vertex in the vertex set is adjacent to exactly ...
in its complement
A complement is something that completes something else.
Complement may refer specifically to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-class ...
).
Construction
 The construction of
The construction of hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s can be imagined the following way:
* 1-dimensional: Two points A and B can be connected to become a line, giving a new line segment AB.
* 2-dimensional: Two parallel line segments AB and CD separated by a distance of AB can be connected to become a square, with the corners marked as ABCD.
* 3-dimensional: Two parallel squares ABCD and EFGH separated by a distance of AB can be connected to become a cube, with the corners marked as ABCDEFGH.
* 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP separated by a distance of AB can be connected to become a tesseract, with the corners marked as ABCDEFGHIJKLMNOP. However, this parallel positioning of two cubes such that their 8 corresponding pairs of vertices are each separated by a distance of AB can only be achieved in a space of 4 or more dimensions.
simplices
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
( irregular 5-cells) that share their vertices with the tesseract. It is known that there are 92487256 such triangulations and that the fewest 4-dimensional simplices in any of them is 16.
The dissection of the tesseract into instances of its characteristic simplex (a particular orthoscheme with Coxeter diagram ) is the most basic direct construction of the tesseract possible. The characteristic 5-cell of the 4-cube is a fundamental region
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each o ...
of the tesseract's defining symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient ...
, the group which generates the B4 polytopes. The tesseract's characteristic simplex directly ''generates'' the tesseract through the actions of the group, by reflecting itself in its own bounding facets (its ''mirror walls'').
Radial equilateral symmetry
The long radius (center to vertex) of the tesseract is equal to its edge length; thus its diagonal through the center (vertex to opposite vertex) is 2 edge lengths. Only a few uniformpolytopes
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
have this property, including the four-dimensional tesseract and 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, the three-dimensional cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...
, and the two-dimensional hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°.
Regular hexa ...
. In particular, the tesseract is the only hypercube (other than a 0-dimensional point) that is ''radially equilateral''. The longest vertex-to-vertex diameter of an ''n''-dimensional hypercube of unit edge length is , so for the square it is , for the cube it is , and only for the tesseract it is , exactly 2 edge lengths.
Formulas
For a tesseract with side length : * Hypervolume: * Surface volume: *Face diagonal
In geometry, a face diagonal of a polyhedron is a diagonal on one of the faces, in contrast to a ''space diagonal'' passing through the interior of the polyhedron.
A cuboid has twelve face diagonals (two on each of the six faces), and it has fou ...
:
* Cell diagonal:
*4-space diagonal:
As a configuration
This configuration matrix represents the tesseract. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole tesseract. The nondiagonal numbers say how many of the column's element occur in or at the row's element. For example, the 2 in the first column of the second row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 4 in the second column of the first row indicates that 4 edges meet at each vertex.Projections
It is possible to project tesseracts into three- and two-dimensional spaces, similarly to projecting a cube into two-dimensional space.
projection
Projection, projections or projective may refer to:
Physics
* Projection (physics), the action/process of light, heat, or sound reflecting from a surface to another in a different direction
* The display of images by a projector
Optics, graphic ...
of the tesseract into three-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining six cells are projected onto the six square faces of the cube.
The ''face-first'' parallel projection of the tesseract into three-dimensional space has a cuboid
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the length of the edges or the angles between edges and faces a cuboid can be transformed into a cub ...
al envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the four remaining cells project to the side faces.
The ''edge-first'' parallel projection of the tesseract into three-dimensional space has an envelope in the shape of a hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices..
Since it has 8 faces, it is an octahedron. However, the term ''octahedron'' is primarily used to ...
. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto six rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The ''vertex-first'' parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedral envelope. Two vertices of the tesseract are projected to the origin. There are exactly two ways of dissecting
Dissection (from Latin ' "to cut to pieces"; also called anatomization) is the dismembering of the body of a deceased animal or plant to study its anatomical structure. Autopsy is used in pathology and forensic medicine to determine the cause of ...
a rhombic dodecahedron into four congruent rhombohedra
In geometry, a rhombohedron (also called a rhombic hexahedron or, inaccurately, a rhomboid) is a three-dimensional figure with six faces which are rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be use ...
, giving a total of eight possible rhombohedra, each a projected cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
of the tesseract. This projection is also the one with maximal volume. One set of projection vectors are ''u''=(1,1,-1,-1), ''v''=(-1,1,-1,1), ''w''=(1,-1,-1,1).

Tessellation
The tesseract, like allhypercubes
In geometry, a hypercube is an N-dimensional space, ''n''-dimensional analogue of a Square (geometry), square () and a cube (). It is a Closed set, closed, Compact space, compact, Convex polytope, convex figure whose 1-N-skeleton, skeleton consis ...
, tessellates Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
. The self-dual tesseractic honeycomb
In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations (or honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of tesseract facets.
Its verte ...
consisting of 4 tesseracts around each face has Schläfli symbol . Hence, the tesseract has a dihedral angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the uni ...
of 90°.
The tesseract's radial equilateral symmetry
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...
makes its tessellation the unique regular body-centered cubic lattice of equal-sized spheres, in any number of dimensions.
Related polytopes and honeycombs
The tesseract is 4th in a series ofhypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
:
The tesseract (8-cell) is the third in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).
As a uniform duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
, the tesseract exists in a sequence of uniform duoprisms: ×.
The regular tesseract, along with the 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
, exists in a set of 15 uniform 4-polytopes with the same symmetry. The tesseract exists in a sequence of regular 4-polytopes and honeycombs, with tetrahedral
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s, . The tesseract is also in a sequence of regular 4-polytope and honeycombs, with cubic cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
.
The regular complex polytope In geometry, a complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one.
A complex polytope may be understood as a collecti ...
42, , in has a real representation as a tesseract or 4-4 duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
in 4-dimensional space. 42 has 16 vertices, and 8 4-edges. Its symmetry is 4 sub>2, order 32. It also has a lower symmetry construction, , or 4×4, with symmetry 4 sub>4, order 16. This is the symmetry if the red and blue 4-edges are considered distinct.
In popular culture
Since their discovery, four-dimensional hypercubes have been a popular theme in art, architecture, and science fiction. Notable examples include: * "And He Built a Crooked House
or AND may refer to:
Logic, grammar, and computing
* Conjunction (grammar), connecting two words, phrases, or clauses
* Logical conjunction in mathematical logic, notated as "∧", "⋅", "&", or simple juxtaposition
* Bitwise AND, a boole ...
", Robert Heinlein
Robert Anson Heinlein (; July 7, 1907 – May 8, 1988) was an American science fiction author, aeronautical engineer, and naval officer. Sometimes called the "dean of science fiction writers", he was among the first to emphasize scientific accu ...
's 1940 science fiction story featuring a building in the form of a four-dimensional hypercube. This and Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis ...
's "The No-Sided Professor", published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle
In topology, a branch of mathematics, the Klein bottle () is an example of a non-orientable surface; it is a two-dimensional manifold against which a system for determining a normal vector cannot be consistently defined. Informally, it is a o ...
, and the hypercube (tesseract).
* ''Crucifixion (Corpus Hypercubus)
''Crucifixion (Corpus Hypercubus)'' is a 1954 oil-on-canvas painting by Salvador Dalí. A nontraditional, surrealist portrayal of the Crucifixion, it depicts Christ on a polyhedron net of a tesseract (hypercube). It is one of his best-known p ...
'', a 1954 oil painting by Salvador Dalí featuring a four-dimensional hypercube unfolded into a three-dimensional Latin cross
A Latin cross or ''crux immissa'' is a type of cross in which the vertical beam sticks above the crossbeam, with the three upper arms either equally long or with the vertical topmost arm shorter than the two horizontal arms, and always with a mu ...
.
* The Grande Arche
La Grande Arche de la Défense (; "The Great Arch of the Defense"), originally called La Grande Arche de la Fraternité (; "Fraternity"), is a monument and building in the business district of La Défense and in the commune of Puteaux, to the west ...
, a monument and building near Paris, France, completed in 1989. According to the monument's engineer, Erik Reitzel
Erik Reitzel (10 May 1941 – 6 February 2012) was a Danish civil engineer who started work in 1964 and was for many years a professor at the Royal Danish Academy of Fine Arts and at the Technical University of Denmark, in the disciplines of bearin ...
, the Grande Arche was designed to resemble the projection of a hypercube.
* ''Fez
Fez most often refers to:
* Fez (hat), a type of felt hat commonly worn in the Ottoman Empire
* Fez, Morocco (or Fes), the second largest city of Morocco
Fez or FEZ may also refer to:
Media
* ''Fez'' (Frank Stella), a 1964 painting by the moder ...
'', a video game where one plays a character who can see beyond the two dimensions other characters can see, and must use this ability to solve platforming puzzles. Features "Dot", a tesseract who helps the player navigate the world and tells how to use abilities, fitting the theme of seeing beyond human perception of known dimensional space.
The word ''tesseract'' was later adopted for numerous other uses in popular culture, including as a plot device in works of science fiction, often with little or no connection to the four-dimensional hypercube of this article. See Tesseract (disambiguation)
A tesseract is a four-dimensional analog of the cube.
Tesseract may also refer to:
Arts and entertainment Literature
* Tesseract, a concept for spacetime travel in the novel ''A Wrinkle in Time'', by Madeleine L'Engle (1962), and subsequent novel ...
.
See also
*Mathematics and art
Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This artic ...
Notes
References
* * F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', Wiley-Interscience Publication** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'',
Mathematische Zeitschrift
''Mathematische Zeitschrift'' (German for ''Mathematical Journal'') is a mathematical journal for pure and applied mathematics published by Springer Verlag.
It was founded in 1918 and edited by Leon Lichtenstein together with Konrad Knopp, Erhard ...
46 (1940) 380–407, MR 2,10]
** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* John H. Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English people, English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to ...
, Heidi Burgiel, Chaim Goodman-Strass (2008) ''The Symmetries of Things'', (Chapter 26. pp. 409: Hemicubes: 1n1)
* T. Gosset (1900) ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics
The ''Messenger of Mathematics'' is a defunct British mathematics journal. The founding editor-in-chief was William Allen Whitworth with Charles Taylor and volumes 1–58 were published between 1872 and 1929. James Whitbread Lee Glaisher was the ...
, Macmillan.
* T. Proctor Hall (1893"The projection of fourfold figures on a three-flat"
American Journal of Mathematics
The ''American Journal of Mathematics'' is a bimonthly mathematics journal published by the Johns Hopkins University Press.
History
The ''American Journal of Mathematics'' is the oldest continuously published mathematical journal in the United ...
15:179–89.
* Norman Johnson ''Uniform Polytopes'', Manuscript (1991)
** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. (1966)
* Victor Schlegel
Victor Schlegel (4 March 1843 – 22 November 1905) was a German mathematician. He is remembered for promoting the geometric algebra of Hermann Grassmann and for a method of visualizing polytopes called Schlegel diagrams.
In the nineteenth centur ...
(1886) ''Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper'', Waren.
External links
* *The Tesseract
Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
Marco Möller's Regular polytopes in ℝ4 (German)
WikiChoron: Tesseract
is an open source program for the
Apple Macintosh
The Mac (known as Macintosh until 1999) is a family of personal computers designed and marketed by Apple Inc. Macs are known for their ease of use and minimalist designs, and are popular among students, creative professionals, and software en ...
(Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
Hypercube 98
A
Windows
Windows is a group of several proprietary graphical operating system families developed and marketed by Microsoft. Each family caters to a certain sector of the computing industry. For example, Windows NT for consumers, Windows Server for serv ...
program that displays animated hypercubes, by Rudy Rucker
Rudolf von Bitter Rucker (; born March 22, 1946) is an American mathematician, computer scientist, science fiction author, and one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known f ...
ken perlin's home page
A way to visualize hypercubes, by
Ken Perlin
Kenneth H. Perlin is a professor in the Department of Computer Science at New York University, founding director of the Media Research Lab at NYU, director of the Future Reality Lab at NYU, and the Director of the Games for Learning Institute. He ...
Some Notes on the Fourth Dimension
includes animated tutorials on several different aspects of the tesseract, b
Davide P. Cervone
{{Polytopes Algebraic topology Four-dimensional geometry 008