4-cube T0123 on:
[Wikipedia]
[Google]
[Amazon]

 In
In
 The construction of
The construction of  The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts ( 16-cells). It can also be
The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts ( 16-cells). It can also be

 The ''cell-first'' parallel graphical projection, projection of the tesseract into three-dimensional space has a cube, cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining six cells are projected onto the six square faces of the cube.
The ''face-first'' parallel projection of the tesseract into three-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the four remaining cells project to the side faces.
The ''edge-first'' parallel projection of the tesseract into three-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto six rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The ''vertex-first'' parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedron, rhombic dodecahedral envelope. Two vertices of the tesseract are projected to the origin. There are exactly two ways of dissection (geometry), dissecting a rhombic dodecahedron into four congruent rhombohedron, rhombohedra, giving a total of eight possible rhombohedra, each a projected
The ''cell-first'' parallel graphical projection, projection of the tesseract into three-dimensional space has a cube, cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining six cells are projected onto the six square faces of the cube.
The ''face-first'' parallel projection of the tesseract into three-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the four remaining cells project to the side faces.
The ''edge-first'' parallel projection of the tesseract into three-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto six rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The ''vertex-first'' parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedron, rhombic dodecahedral envelope. Two vertices of the tesseract are projected to the origin. There are exactly two ways of dissection (geometry), dissecting a rhombic dodecahedron into four congruent rhombohedron, rhombohedra, giving a total of eight possible rhombohedra, each a projected 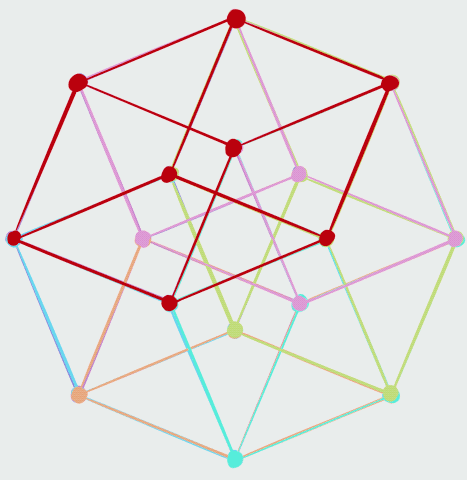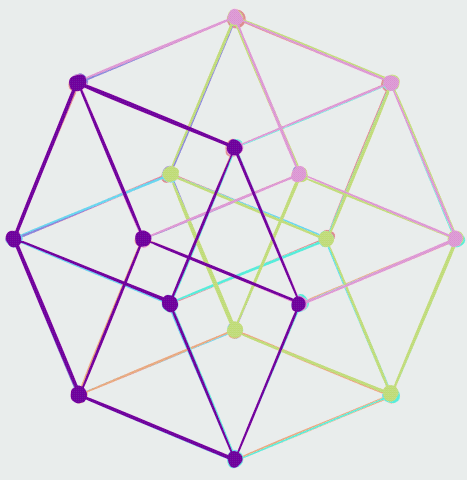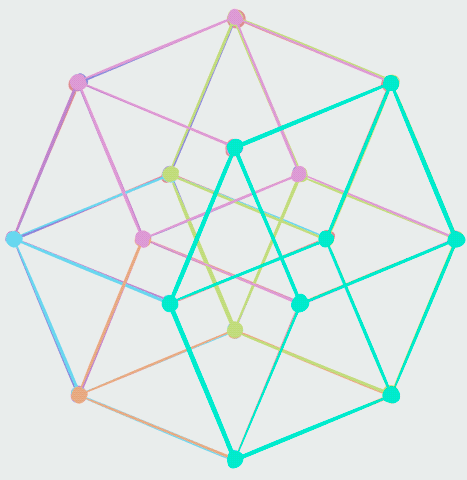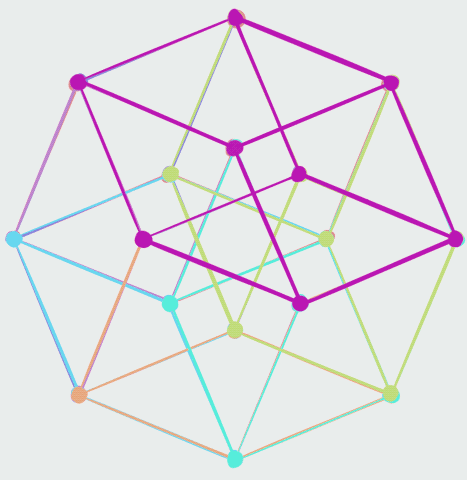
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10] ** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', [Math. Zeit. 188 (1985) 559-591] ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45] * John Horton Conway, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass (2008) ''The Symmetries of Things'', (Chapter 26. pp. 409: Hemicubes: 1n1) * Thorold Gosset, T. Gosset (1900) ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan. * T. Proctor Hall (1893
"The projection of fourfold figures on a three-flat"
American Journal of Mathematics 15:179–89. * Norman Johnson (mathematician), Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. (1966) * Victor Schlegel (1886) ''Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper'', Waren.
The Tesseract
Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
Marco Möller's Regular polytopes in ℝ4 (German)
WikiChoron: Tesseract
is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
Hypercube 98
A Microsoft Windows, Windows program that displays animated hypercubes, by Rudy Rucker
ken perlin's home page
A way to visualize hypercubes, by Ken Perlin
Some Notes on the Fourth Dimension
includes animated tutorials on several different aspects of the tesseract, b
Davide P. Cervone
{{Polytopes Algebraic topology Four-dimensional geometry 4-polytopes, 008

 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a tesseract is the four-dimensional
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
analogue of the cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
; the tesseract is to the cube as the cube is to the square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
. Just as the surface of the cube consists of six square faces
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affe ...
, the hypersurface
In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidean ...
of the tesseract consists of eight cubical cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
. The tesseract is one of the six convex regular 4-polytope
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six convex and ten star regu ...
s.
The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s or measure polytopes. Coxeter labels it the polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
.
The ''Oxford English Dictionary
The ''Oxford English Dictionary'' (''OED'') is the first and foundational historical dictionary of the English language, published by Oxford University Press (OUP). It traces the historical development of the English language, providing a com ...
'' traces the word ''tesseract'' to Charles Howard Hinton
Charles Howard Hinton (1853 – 30 April 1907) was a British mathematician and writer of science fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imaginative and ...
's 1888 book ''A New Era of Thought
''A New Era of Thought'' is a non-fiction work written by Charles Howard Hinton, published in 1888 and reprinted in 1900 by Swan Sonnenschein & Co. Ltd., London. ''A New Era of Thought'' is about the fourth dimension and its implications on human ...
''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled the word as ''tessaract''.
Geometry
As aregular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or -faces (for all , where is the dimension of the polytope) — cells, f ...
with three cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
s folded together around every edge, it has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
with hyperoctahedral symmetry of order 384. Constructed as a 4D hyperprism
In geometry, a prism is a polyhedron comprising an polygon base, a second base which is a translated copy (rigidly moved without rotation) of the first, and other faces, necessarily all parallelograms, joining corresponding sides of the two ba ...
made of two parallel cubes, it can be named as a composite Schläfli symbol × , with symmetry order 96. As a 4-4 duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
, a Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ti ...
of two squares
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
, it can be named by a composite Schläfli symbol ×, with symmetry order 64. As an orthotope
In geometry, an orthotopeCoxeter, 1973 (also called a hyperrectangle or a box) is the generalization of a rectangle to higher dimensions.
A necessary and sufficient condition is that it is Congruence (geometry), congruent to the Cartesian product ...
it can be represented by composite Schläfli symbol × × × or 4, with symmetry order 16.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
of the tesseract is a regular tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
. The dual polytope
In geometry, every polyhedron is associated with a second dual structure, where the Vertex (geometry), vertices of one correspond to the Face (geometry), faces of the other, and the edges between pairs of vertices of one correspond to the edges b ...
of the tesseract is the 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
with Schläfli symbol , with which it can be combined to form the compound of tesseract and 16-cell
In 4-dimensional geometry, the tesseract 16-cell compound is a polytope compound composed of a regular tesseract and its dual, the regular 16-cell. Its convex hull is the regular 24-cell, which is self-dual.
A '' compound polytope'' is a figure t ...
.
Each edge of a regular tesseract is of the same length. This is of interest when using tesseracts as the basis for a network topology
Network topology is the arrangement of the elements ( links, nodes, etc.) of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, including command and contro ...
to link multiple processors in parallel computing
Parallel computing is a type of computation in which many calculations or processes are carried out simultaneously. Large problems can often be divided into smaller ones, which can then be solved at the same time. There are several different fo ...
: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Coordinates
The standard tesseract inEuclidean 4-space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
is given as the convex hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space ...
of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
:
In this Cartesian frame of reference, the tesseract has radius 2 and is bounded by eight hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
s (''x''i = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Net
An unfolding of apolytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
is called a net. There are 261 distinct nets of the tesseract. The unfoldings of the tesseract can be counted by mapping the nets to ''paired trees'' (a tree
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, including only woody plants with secondary growth, plants that are ...
together with a perfect matching
In graph theory, a perfect matching in a graph is a matching that covers every vertex of the graph. More formally, given a graph , a perfect matching in is a subset of edge set , such that every vertex in the vertex set is adjacent to exactly ...
in its complement).
Construction
 The construction of
The construction of hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s can be imagined the following way:
* 1-dimensional: Two points A and B can be connected to become a line, giving a new line segment AB.
* 2-dimensional: Two parallel line segments AB and CD separated by a distance of AB can be connected to become a square, with the corners marked as ABCD.
* 3-dimensional: Two parallel squares ABCD and EFGH separated by a distance of AB can be connected to become a cube, with the corners marked as ABCDEFGH.
* 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP separated by a distance of AB can be connected to become a tesseract, with the corners marked as ABCDEFGHIJKLMNOP. However, this parallel positioning of two cubes such that their 8 corresponding pairs of vertices are each separated by a distance of AB can only be achieved in a space of 4 or more dimensions.
triangulated
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points.
Applications
In surveying
Specifically in surveying, triangulation involves only angle me ...
into 4-dimensional simplices
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
( irregular 5-cells) that share their vertices with the tesseract. It is known that there are 92487256 such triangulations and that the fewest 4-dimensional simplices in any of them is 16.
The dissection of the tesseract into instances of its characteristic simplex (a particular orthoscheme with Coxeter diagram ) is the most basic direct construction of the tesseract possible. The characteristic 5-cell of the 4-cube is a fundamental region of the tesseract's defining symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient ...
, the group which generates the B4 polytope, B4 polytopes. The tesseract's characteristic simplex directly ''generates'' the tesseract through the actions of the group, by reflecting itself in its own bounding facets (its ''mirror walls'').
Radial equilateral symmetry
The long radius (center to vertex) of the tesseract is equal to its edge length; thus its diagonal through the center (vertex to opposite vertex) is 2 edge lengths. Only a few uniform polytopes have this property, including the four-dimensional tesseract and 24-cell#Radially equilateral honeycomb, 24-cell, the three-dimensional Cuboctahedron#Radial equilateral symmetry, cuboctahedron, and the two-dimensional hexagon. In particular, the tesseract is the only hypercube (other than a 0-dimensional point) that is ''radially equilateral''. The longest vertex-to-vertex diameter of an ''n''-dimensional hypercube of unit edge length is , so for the square it is , for the cube it is , and only for the tesseract it is , exactly 2 edge lengths.Formulas
For a tesseract with side length : * Hypervolume: * Surface volume: *Face diagonal: *Space diagonal, Cell diagonal: *4-space diagonal:As a configuration
This Regular 4-polytope#As configurations, configuration matrix represents the tesseract. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole tesseract. The nondiagonal numbers say how many of the column's element occur in or at the row's element. For example, the 2 in the first column of the second row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 4 in the second column of the first row indicates that 4 edges meet at each vertex.Projections
It is possible to project tesseracts into three- and two-dimensional spaces, similarly to projecting a cube into two-dimensional space.
cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
of the tesseract. This projection is also the one with maximal volume. One set of projection vectors are ''u''=(1,1,-1,-1), ''v''=(-1,1,-1,1), ''w''=(1,-1,-1,1).

Tessellation
The tesseract, like all hypercubes, tessellates Euclidean space. The self-dual tesseractic honeycomb consisting of 4 tesseracts around each face has Ludwig Schläfli, Schläfli symbol . Hence, the tesseract has a dihedral angle of 90°. The tesseract's #Radial equilateral symmetry, radial equilateral symmetry makes its tessellation the Tesseractic honeycomb#Sphere packing, unique regular body-centered cubic lattice of equal-sized spheres, in any number of dimensions.Related polytopes and honeycombs
The tesseract is 4th in a series ofhypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
:
The tesseract (8-cell) is the third in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).
As a uniform duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
, the tesseract exists in a Uniform 4-polytope#Polygonal prismatic prisms: .5Bp.5D .C3.97 .5B .5D .C3.97 .5B .5D, sequence of uniform duoprisms: ×.
The regular tesseract, along with the 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
, exists in a set of 15 Truncated tesseract#Related uniform polytopes in tesseract symmetry, uniform 4-polytopes with the same symmetry. The tesseract exists in a Hexagonal tiling honeycomb#Polytopes and honeycombs with tetrahedral vertex figures, sequence of regular 4-polytopes and honeycombs, with tetrahedron, tetrahedral vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s, . The tesseract is also in a Order-5 cubic honeycomb#Related polytopes and honeycombs with cubic cells, sequence of regular 4-polytope and honeycombs, with cube, cubic cell (geometry), cells.
The regular complex polytope 42, , in has a real representation as a tesseract or 4-4 duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
in 4-dimensional space. 42 has 16 vertices, and 8 4-edges. Its symmetry is 4[4]2, order 32. It also has a lower symmetry construction, , or 4×4, with symmetry 4[2]4, order 16. This is the symmetry if the red and blue 4-edges are considered distinct.
In popular culture
Since their discovery, four-dimensional hypercubes have been a popular theme in art, architecture, and science fiction. Notable examples include: * "And He Built a Crooked House", Robert A. Heinlein, Robert Heinlein's 1940 science fiction story featuring a building in the form of a four-dimensional hypercube. This and Martin Gardner's "The No-Sided Professor", published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle, and the hypercube (tesseract). * ''Crucifixion (Corpus Hypercubus)'', a 1954 oil painting by Salvador Dalí featuring a four-dimensional hypercube unfolded into a three-dimensional Latin cross. * The Grande Arche, a monument and building near Paris, France, completed in 1989. According to the monument's engineer, Erik Reitzel, the Grande Arche was designed to resemble the projection of a hypercube. * ''Fez (video game), Fez'', a video game where one plays a character who can see beyond the two dimensions other characters can see, and must use this ability to solve platforming puzzles. Features "Dot", a tesseract who helps the player navigate the world and tells how to use abilities, fitting the theme of seeing beyond human perception of known dimensional space. The word ''tesseract'' was later adopted for numerous other uses in popular culture, including as a plot device in works of science fiction, often with little or no connection to the four-dimensional hypercube of this article. See Tesseract (disambiguation).See also
* Mathematics and artNotes
References
* * F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', Wiley-Interscience Publication** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10] ** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', [Math. Zeit. 188 (1985) 559-591] ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45] * John Horton Conway, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass (2008) ''The Symmetries of Things'', (Chapter 26. pp. 409: Hemicubes: 1n1) * Thorold Gosset, T. Gosset (1900) ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan. * T. Proctor Hall (1893
"The projection of fourfold figures on a three-flat"
American Journal of Mathematics 15:179–89. * Norman Johnson (mathematician), Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. (1966) * Victor Schlegel (1886) ''Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper'', Waren.
External links
* *The Tesseract
Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
Marco Möller's Regular polytopes in ℝ4 (German)
WikiChoron: Tesseract
is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
Hypercube 98
A Microsoft Windows, Windows program that displays animated hypercubes, by Rudy Rucker
ken perlin's home page
A way to visualize hypercubes, by Ken Perlin
Some Notes on the Fourth Dimension
includes animated tutorials on several different aspects of the tesseract, b
Davide P. Cervone
{{Polytopes Algebraic topology Four-dimensional geometry 4-polytopes, 008