24 канал on:
[Wikipedia]
[Google]
[Amazon]
4 (four) is a

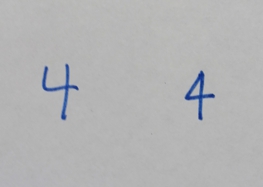 Brahmic numerals represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga Empire, Shunga would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arabs' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross.
While the shape of the character for the digit 4 has an ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in
Brahmic numerals represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga Empire, Shunga would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arabs' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross.
While the shape of the character for the digit 4 has an ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in  .
.
 On the seven-segment displays of pocket calculators and digital watches, as well as certain optical character recognition fonts, 4 is seen with an open top.
Television stations that operate on channel 4 (disambiguation), channel 4 have occasionally made use of another variation of the "open 4", with the open portion being on the side, rather than the top. This version resembles the Canadian Aboriginal syllabics letter ᔦ. The magnetic ink character recognition "CMC-7" font also uses this variety of "4".
On the seven-segment displays of pocket calculators and digital watches, as well as certain optical character recognition fonts, 4 is seen with an open top.
Television stations that operate on channel 4 (disambiguation), channel 4 have occasionally made use of another variation of the "open 4", with the open portion being on the side, rather than the top. This version resembles the Canadian Aboriginal syllabics letter ᔦ. The magnetic ink character recognition "CMC-7" font also uses this variety of "4".
 *The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The Square of Opposition, in both its Aristotelian version and its Square of Opposition#Modern squares of opposition, Boolean version, consists of four forms: A ("All ''S'' is ''R''"), I ("Some ''S'' is ''R''"), E ("No ''S'' is ''R''"), and O ("Some ''S'' is not ''R''").
*In regard to whether two given propositions can have the same truth value, there are four separate logical possibilities: the propositions are ''subalterns'' (possibly both are true, and possibly both are false); ''subcontraries'' (both may be true, but not that both are false); ''contraries'' (both may be false, but not that both are true); or ''contradictories'' (it is not possible that both are true, and it is not possible that both are false).
*Aristotle held that there are basically four causes in nature: the Four causes#Material cause, material, the Four causes#Formal cause, formal, the Four causes#Efficient cause, efficient, and the Four causes#Final cause, final.
*The Stoicism, Stoics held with four basic categories (Stoic), categories, all viewed as bodies (substantial and insubstantial): (1) ''substance'' in the sense of substrate, primary formless matter; (2) ''quality'', matter's organization to differentiate and individualize something, and coming down to a physical ingredient such as ''pneuma'', breath; (3) ''somehow holding'' (or ''disposed''), as in a posture, state, shape, size, action, and (4) ''somehow holding'' (or ''disposed'') ''toward something,'' as in relative location, familial relation, and so forth.
*Immanuel Kant expounded a Category (Kant)#The table of judgments, table of judgments involving four three-way alternatives, in regard to (1) Quantity, (2) Quality, (3) Relation, (4) Modality, and, based thereupon, a Category (Kant)#The table of categories, table of four categories, named by the terms just listed, and each with three subcategories.
*Arthur Schopenhauer's doctoral thesis was ''On the Fourfold Root of the Principle of Sufficient Reason''.
*Franz Brentano held that any major philosophical period has four phases: (1) Creative and rapidly progressing with scientific interest and results; then declining through the remaining phases, (2) practical, (3) increasingly skeptical, and (4) literary, mystical, and scientifically worthless—until philosophy is renewed through a new period's first phase. (See Brentano's essay "The Four Phases of Philosophy and Its Current State" 1895, tr. by Mezei and Smith 1998.)
*Charles Sanders Peirce, C. S. Peirce, usually a trichotomy (philosophy), trichotomist, discussed four methods for overcoming troublesome uncertainties and achieving secure beliefs: (1) the method of tenacity (policy of sticking to initial belief), (2) the method of authority, (3) the method of congruity (following a fashionable paradigm), and (4) the Fallibilism, fallibilistic, self-correcting method of science (see "s:The Fixation of Belief, The Fixation of Belief", 1877); and four barriers to inquiry, barriers refused by the fallibilist: (1) assertion of absolute certainty; (2) maintaining that something is unknowable; (3) maintaining that something is inexplicable because absolutely basic or ultimate; (4) holding that perfect exactitude is possible, especially such as to quite preclude unusual and anomalous phenomena (see
*The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The Square of Opposition, in both its Aristotelian version and its Square of Opposition#Modern squares of opposition, Boolean version, consists of four forms: A ("All ''S'' is ''R''"), I ("Some ''S'' is ''R''"), E ("No ''S'' is ''R''"), and O ("Some ''S'' is not ''R''").
*In regard to whether two given propositions can have the same truth value, there are four separate logical possibilities: the propositions are ''subalterns'' (possibly both are true, and possibly both are false); ''subcontraries'' (both may be true, but not that both are false); ''contraries'' (both may be false, but not that both are true); or ''contradictories'' (it is not possible that both are true, and it is not possible that both are false).
*Aristotle held that there are basically four causes in nature: the Four causes#Material cause, material, the Four causes#Formal cause, formal, the Four causes#Efficient cause, efficient, and the Four causes#Final cause, final.
*The Stoicism, Stoics held with four basic categories (Stoic), categories, all viewed as bodies (substantial and insubstantial): (1) ''substance'' in the sense of substrate, primary formless matter; (2) ''quality'', matter's organization to differentiate and individualize something, and coming down to a physical ingredient such as ''pneuma'', breath; (3) ''somehow holding'' (or ''disposed''), as in a posture, state, shape, size, action, and (4) ''somehow holding'' (or ''disposed'') ''toward something,'' as in relative location, familial relation, and so forth.
*Immanuel Kant expounded a Category (Kant)#The table of judgments, table of judgments involving four three-way alternatives, in regard to (1) Quantity, (2) Quality, (3) Relation, (4) Modality, and, based thereupon, a Category (Kant)#The table of categories, table of four categories, named by the terms just listed, and each with three subcategories.
*Arthur Schopenhauer's doctoral thesis was ''On the Fourfold Root of the Principle of Sufficient Reason''.
*Franz Brentano held that any major philosophical period has four phases: (1) Creative and rapidly progressing with scientific interest and results; then declining through the remaining phases, (2) practical, (3) increasingly skeptical, and (4) literary, mystical, and scientifically worthless—until philosophy is renewed through a new period's first phase. (See Brentano's essay "The Four Phases of Philosophy and Its Current State" 1895, tr. by Mezei and Smith 1998.)
*Charles Sanders Peirce, C. S. Peirce, usually a trichotomy (philosophy), trichotomist, discussed four methods for overcoming troublesome uncertainties and achieving secure beliefs: (1) the method of tenacity (policy of sticking to initial belief), (2) the method of authority, (3) the method of congruity (following a fashionable paradigm), and (4) the Fallibilism, fallibilistic, self-correcting method of science (see "s:The Fixation of Belief, The Fixation of Belief", 1877); and four barriers to inquiry, barriers refused by the fallibilist: (1) assertion of absolute certainty; (2) maintaining that something is unknowable; (3) maintaining that something is inexplicable because absolutely basic or ultimate; (4) holding that perfect exactitude is possible, especially such as to quite preclude unusual and anomalous phenomena (see
F.R.L.
[First Rule of Logic], 1899). *Paul Weiss (philosopher), Paul Weiss built a system involving four modes of being: Actualities (substances in the sense of substantial, spatiotemporally finite beings), Ideality or Possibility (pure normative form), Existence (the dynamic field), and God (unity). (See Weiss's ''Modes of Being'', 1958). *Karl Popper outlined a tetradic schema to describe the growth of theories and, via generalization, also the emergence of new behaviors and living organisms: (1) problem, (2) tentative theory, (3) (attempted) error-elimination (especially by way of critical discussion), and (4) new problem(s). (See Popper's ''Objective Knowledge'', 1972, revised 1979.) *John Boyd (military strategist) made his key concept the decision cycle or John Boyd (military strategist)#OODA loop, OODA loop, consisting of four stages: (1) observation (data intake through the senses), (2) orientation (analysis and synthesis of data), (3) decision, and (4) action. Boyd held that his decision cycle has philosophical generality, though for strategists the point remains that, through swift decisions, one can disrupt an opponent's decision cycle. *Richard McKeon outlined four classes (each with four subclasses) of modes of philosophical inquiry: (1) Modes of Being (Being); (2) Modes of Thought (That which is); (3) Modes of Fact (Existence); (4) Modes of Simplicity (Experience)—and, corresponding to them, four classes (each with four subclasses) of philosophical semantics: Principles, Methods, Interpretations, and Selections. (See McKeon's "Philosophic Semantics and Philosophic Inquiry" in ''Freedom and History and Other Essays'', 1989.) *Jonathan Lowe (E.J. Lowe) argues in ''The Four-Category Ontology'', 2006, for four categories: ''kinds'' (substantial universals), ''attributes'' (relational universals and property-universals), ''objects'' (substantial particulars), and ''modes'' (relational particulars and property-particulars, also known as "trope (philosophy), tropes"). (See Lowe's "Recent Advances in Metaphysics," 2001
Eprint
*Four opposed camps of the morality and nature of evil: moral absolutism, amoralism, moral relativism, and moral universalism.
 *The resin identification code used in recycling to identify low-density polyethylene.
*Most furniture has four legs – tables, chairs, etc.
*The four color process (CMYK) is used for printing.
*Wide use of
*The resin identification code used in recycling to identify low-density polyethylene.
*Most furniture has four legs – tables, chairs, etc.
*The four color process (CMYK) is used for printing.
*Wide use of
 *Many internal combustion engines are called four-stroke engines because they complete one thermodynamic cycle in four distinct steps: Intake, compression, power, and exhaust.
*Most vehicles, including motor vehicles, and particularly automobile, cars/automobiles and light commercial vehicles have four road wheels.
*"quattro (four wheel drive system), Quattro", meaning four in the Italian language, is used by Audi as a trademark to indicate that all-wheel drive (AWD) technologies are used on Audi-branded cars. The word "Quattro" was initially used by Audi in 1980 in its original 4WD coupé, the Audi Quattro. Audi also has a privately held subsidiary company called quattro GmbH.
*List of highways numbered 4
*Many internal combustion engines are called four-stroke engines because they complete one thermodynamic cycle in four distinct steps: Intake, compression, power, and exhaust.
*Most vehicles, including motor vehicles, and particularly automobile, cars/automobiles and light commercial vehicles have four road wheels.
*"quattro (four wheel drive system), Quattro", meaning four in the Italian language, is used by Audi as a trademark to indicate that all-wheel drive (AWD) technologies are used on Audi-branded cars. The word "Quattro" was initially used by Audi in 1980 in its original 4WD coupé, the Audi Quattro. Audi also has a privately held subsidiary company called quattro GmbH.
*List of highways numbered 4
 * The phrase "four-letter word" is used to describe many profanity, swear words in the English language.
*Four is the only number whose name in English has the same number of letters as its value.
*Four (, formal writing: , pinyin sì) is considered an unlucky number in Chinese culture, Chinese, Korean culture, Korean, Culture of Vietnam, Vietnamese and Culture of Japan, Japanese cultures mostly in Eastern Asia because it sounds like the word "death" (, pinyin sǐ). To avoid complaints from people with tetraphobia, many numbered product lines skip the "four": e.g. Nokia cell phones (there was no series beginning with a 4 until the Nokia 4.2), PalmOne, Inc., Palm Personal digital assistant, PDAs, etc. Some buildings skip floor 4 or replace the number with the letter "F", particularly in heavily Asian areas. ''See tetraphobia'' and ''Numbers in Chinese culture''.
*In Pythagorean numerology (a pseudocience) the number 4 represents security and stability.
*The number of characters in a canonical four-character idiom (disambiguation), four-character idiom.
*In the ICAO spelling alphabet, NATO phonetic alphabet, the digit 4 is called "fower".
*In astrology, Cancer (constellation), Cancer is the 4th astrological sign of the Zodiac.
*In Tarot, The Emperor (Tarot card), The Emperor is the fourth trump (card games), trump or Major Arcana card.
*In ''Tetris'', a game named for the Greek word for 4, every shape in the game is formed of 4 blocks each.
*4 represents the number of Justices on the Supreme Court of the United States necessary to grant a writ of certiorari (i.e., agree to hear a case; it is one less than the number necessary to render a majority decision) at the court's current size.
*Number Four is a character in the book series ''Lorien Legacies.''
*In the performing arts, the fourth wall is an imaginary barrier which separates the audience from the performers, and is "broken" when performers communicate directly to the audience.
* The phrase "four-letter word" is used to describe many profanity, swear words in the English language.
*Four is the only number whose name in English has the same number of letters as its value.
*Four (, formal writing: , pinyin sì) is considered an unlucky number in Chinese culture, Chinese, Korean culture, Korean, Culture of Vietnam, Vietnamese and Culture of Japan, Japanese cultures mostly in Eastern Asia because it sounds like the word "death" (, pinyin sǐ). To avoid complaints from people with tetraphobia, many numbered product lines skip the "four": e.g. Nokia cell phones (there was no series beginning with a 4 until the Nokia 4.2), PalmOne, Inc., Palm Personal digital assistant, PDAs, etc. Some buildings skip floor 4 or replace the number with the letter "F", particularly in heavily Asian areas. ''See tetraphobia'' and ''Numbers in Chinese culture''.
*In Pythagorean numerology (a pseudocience) the number 4 represents security and stability.
*The number of characters in a canonical four-character idiom (disambiguation), four-character idiom.
*In the ICAO spelling alphabet, NATO phonetic alphabet, the digit 4 is called "fower".
*In astrology, Cancer (constellation), Cancer is the 4th astrological sign of the Zodiac.
*In Tarot, The Emperor (Tarot card), The Emperor is the fourth trump (card games), trump or Major Arcana card.
*In ''Tetris'', a game named for the Greek word for 4, every shape in the game is formed of 4 blocks each.
*4 represents the number of Justices on the Supreme Court of the United States necessary to grant a writ of certiorari (i.e., agree to hear a case; it is one less than the number necessary to render a majority decision) at the court's current size.
*Number Four is a character in the book series ''Lorien Legacies.''
*In the performing arts, the fourth wall is an imaginary barrier which separates the audience from the performers, and is "broken" when performers communicate directly to the audience.
Marijn.Org on Why is everything four?
by Penelope Merritt at samuel-beckett.net
The Number 4The Positive Integer 4
{{Authority control Integers 4 (number),
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
, numeral and digit. It is the natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
following 3 and preceding 5. It is the smallest semiprime
In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers.
Because there are infinitely many prime nu ...
and composite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
, and is considered unlucky in many East Asian cultures.
In mathematics
Four is the smallestcomposite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
, its proper divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
s being and . Four is the sum and product of two
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultur ...
with itself: + = = x , the only number such that + = = x , which also makes four the smallest squared prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. In Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976.
In his 1947 paper, R. L. Goodstein introduced the specific sequence of operations that are now called ''hyperoperati ...
, , and so forth, for any number of up arrows. By consequence, four is the only square one more than a prime number, specifically three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
. The sum of the first four prime numbers two
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultur ...
+ three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
+ five
5 is a number, numeral, and glyph.
5, five or number 5 may also refer to:
* AD 5, the fifth year of the AD era
* 5 BC, the fifth year before the AD era
Literature
* ''5'' (visual novel), a 2008 visual novel by Ram
* ''5'' (comics), an awa ...
+ seven
7 is a number, numeral, and glyph.
7 or seven may also refer to:
* AD 7, the seventh year of the AD era
* 7 BC, the seventh year before the AD era
* The month of
July
Music Artists
* Seven (Swiss singer) (born 1978), a Swiss recording artist ...
is the only sum of four consecutive prime numbers that yields an odd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
prime number, seventeen
Seventeen or 17 may refer to:
*17 (number), the natural number following 16 and preceding 18
* one of the years 17 BC, AD 17, 1917, 2017
Literature
Magazines
* ''Seventeen'' (American magazine), an American magazine
* ''Seventeen'' (Japanese m ...
, which is the fourth super-prime
Super-prime numbers, also known as higher-order primes or prime-indexed primes (PIPs), are the subsequence of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers.
The subsequence begins
:3, 5, 11, 17, 31, ...
. Four lies between the first proper pair of twin primes
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term ''twin pr ...
, three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
and five
5 is a number, numeral, and glyph.
5, five or number 5 may also refer to:
* AD 5, the fifth year of the AD era
* 5 BC, the fifth year before the AD era
Literature
* ''5'' (visual novel), a 2008 visual novel by Ram
* ''5'' (comics), an awa ...
, which are the first two Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
s, like seventeen
Seventeen or 17 may refer to:
*17 (number), the natural number following 16 and preceding 18
* one of the years 17 BC, AD 17, 1917, 2017
Literature
Magazines
* ''Seventeen'' (American magazine), an American magazine
* ''Seventeen'' (Japanese m ...
, which is the third. On the other hand, the square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
of four 42, equivalently the fourth power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So:
:''n''4 = ''n'' × ''n'' × ''n'' × ''n''
Fourth powers are also formed by multiplying a number by its cube. Further ...
of two 24, is sixteen; the only number that has = as a form of factorization
In mathematics, factorization (or factorisation, see American and British English spelling differences#-ise, -ize (-isation, -ization), English spelling differences) or factoring consists of writing a number or another mathematical object as a p ...
. Holistically, there are four elementary arithmetic operations in mathematics: addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
(+), subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
(−), multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
(×), and division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
(÷); and four basic number system
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
s, the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real ...
s , rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
s , integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s , and natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
s .
Each natural number divisible by 4 is a difference of squares of two natural numbers, i.e. = − . A number is a multiple of 4 if its last two digits are a multiple of 4. For example, 1092 is a multiple of 4 because .
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as the sum of four integer squares. That is, the squares form an additive basis of order four.
p = a_0^2 + a_1^2 + a_2^2 + a_ ...
states that every positive integer can be written as the sum of at most four square number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
s. Three are not always sufficient; for instance cannot be written as the sum of three squares.
There are four all-Harshad number
In mathematics, a harshad number (or Niven number) in a given number base is an integer that is divisible by the sum of its digits when written in that base.
Harshad numbers in base are also known as -harshad (or -Niven) numbers.
Harshad number ...
s: 1, 2, ''4'', and 6. 12, which is divisible by four thrice over, is a Harshad number in all bases except octal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, ...
.
A four-sided plane figure is a quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
or quadrangle, sometimes also called a ''tetragon''. It can be further classified as a rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
or ''oblong'', kite
A kite is a tethered heavier than air flight, heavier-than-air or lighter-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. ...
, rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The ...
, and square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
.
Four is the highest degree general polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation' ...
for which there is a solution in radicals
A solution in radicals or algebraic solution is a closed-form expression, and more specifically a closed-form algebraic expression, that is the solution of a polynomial equation, and relies only on addition, subtraction, multiplication, divi ...
.
The four-color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions sha ...
states that a planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross ...
(or, equivalently, a flat map
A map is a symbolic depiction emphasizing relationships between elements of some space, such as objects, regions, or themes.
Many maps are static, fixed to paper or some other durable medium, while others are dynamic or interactive. Although ...
of two-dimensional regions such as countries) can be colored using four colors, so that adjacent vertices (or regions) are always different colors. Three colors are not, in general, sufficient to guarantee this. The largest planar complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is c ...
has four vertices.
A solid figure with four faces as well as four vertices is a tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, which is the smallest possible number of faces and vertices a polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on th ...
can have. The regular tetrahedron, also called a 3-simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
, is the simplest Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
. It has four regular triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each othe ...
s as faces that are themselves at dual positions with the vertices of another tetrahedron. Tetrahedra can be inscribed inside all other four Platonic solids, and tessellate space alongside the regular octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...
in the alternated cubic honeycomb
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
Other names incl ...
.
Four-dimensional space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
is the highest-dimensional space featuring more than three regular convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
figures:
*Two-dimensional: infinitely many regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
s.
*Three-dimensional: five regular polyhedra
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equival ...
; the five Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
s which are the tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
, octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...
, dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
, and icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
.
*Four-dimensional: six regular polychora
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six convex and ten star regu ...
; the 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
, 8-cell or tesseract
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eig ...
, 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
, 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, heca ...
, and 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
. The 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, made of regular octahedra
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...
, has no analogue in any other dimension; it is self-dual
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a Injective function, one-to-one fashion, often (but not always) by means of an Involution (mathematics), involutio ...
, with its 24-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular polytope, regular space-filling tessellation (or honeycomb (geometry), honeycomb) of 4-dimensional Euclidean space by ...
dual to the 16-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensiona ...
.
*Five-dimensional and every higher dimension: three regular convex -polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
s, all within the infinite family of regular -simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
es, -hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s, and - orthoplexes.
The fourth dimension is also the highest dimension where regular self-intersecting figures exist:
*Two-dimensional: infinitaly many regular star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations ...
s.
*Three-dimensional: ''four'' regular star polyhedra
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
There are two general kinds of star polyhedron:
*Polyhedra which self-intersect in a repetitive way.
*Concave p ...
, the regular Kepler-Poinsot star polyhedra.
*Four-dimensional: ten regular star polychora, the Schläfli–Hess star polychora. They contain cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
of Kepler-Poinsot polyhedra alongside regular tetrahedra, icosahedra
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
and dodecahedra
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
.
*Five-dimensional and every higher dimension: zero regular star-polytopes; uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, se ...
star polytopes in dimensions > are the most symmetric, which mainly originate from stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific el ...
s of regular -polytopes.
Altogether, sixteen (or 16 = 42) regular convex and star polychora are generated from symmetries of ''four'' (4) Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections th ...
s and point groups
In geometry, a point group is a mathematical group of symmetry operations (isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every p ...
in the fourth dimension: the simplex, hypercube, icositetrachoric, and hexacosichoric groups; with the demihypercube
In geometry, demihypercubes (also called ''n-demicubes'', ''n-hemicubes'', and ''half measure polytopes'') are a class of ''n''-polytopes constructed from alternation of an ''n''-hypercube, labeled as ''hγn'' for being ''half'' of the hype ...
group generating two alternative constructions.
There are also sixty-four (or 64 = 43) four-dimensional Bravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n_ ...
s, ''and'' sixty-four Uniform 4-polytope, uniform polychora in the fourth dimension based on the same , , and Point groups in four dimensions, Coxeter groups, and extending to Uniform 4-polytope#Prismatic uniform 4-polytopes, prismatic groups of Uniform polyhedron, uniform polyhedra, including one special Wythoff construction, non-Wythoffian form, the grand antiprism. There are also two infinite families of duoprisms and Uniform antiprismatic prism, antiprismatic prisms in the fourth dimension.
Four-dimensional differential manifolds have some unique properties. There is only one differential structure on except when = , in which case there are uncountably many.
The smallest non-cyclic group has four elements; it is the Klein four-group. ''A'' alternating groups are not simple group, simple for values ≤ .
Further extensions of the real numbers under Hurwitz's theorem (composition algebras), Hurwitz's theorem states that there are four Normed algebra, normed division algebras: the real numbers , the complex numbers , the quaternions , and the octonions . Under Cayley–Dickson constructions, the sedenions constitute a further fourth extension over . The real numbers are Ordered field, ordered, commutative and associative Algebraic structure, algebras, as well as alternative algebras with power-associativity. The complex numbers share all four multiplicative algebraic properties of the reals , without being ordered. The quaternions loose a further commutative algebraic property, while holding associative, alternative, and power-associative properties. The octonions are alternative and power-associative, while the sedenions are only power-associative. The sedenions and all further ''extensions'' of these four normed division algebras are solely power-associative with non-trivial zero divisors, which makes them Division algebra, non-division algebras. has a vector space of dimension 1, while , , and work in algebraic number fields of dimensions 2, 4, 8, and 16, respectively.
List of basic calculations
Evolution of the Hindu-Arabic digit

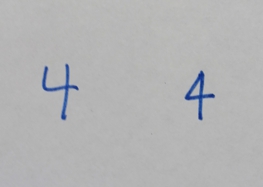 Brahmic numerals represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga Empire, Shunga would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arabs' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross.
While the shape of the character for the digit 4 has an ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in
Brahmic numerals represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga Empire, Shunga would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arabs' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross.
While the shape of the character for the digit 4 has an ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in In religion
Buddhism
*Four Noble Truths – Dukkha, Pratītyasamutpāda, Samudaya, Nirvana, Nirodha, Noble Eightfold Path, Magga *Four sights – observations which affected Prince Siddhartha deeply and made him realize the sufferings of all beings, and compelled him to begin his spiritual journey—an old age, old man, a illness, sick man, a death, dead man, and an ascetic *Mahābhūta, Four Great Elements – earth (classical element), earth, water (classical element), water, fire (classical element), fire, and air (classical element), wind *Four Heavenly Kings *Satipatthana, Four Foundations of Mindfulness – contemplation of the body, contemplation of feelings, contemplation of mind, contemplation of mental objects *Four Right Exertions *Iddhipada, Four Bases of Power *Jhāna, Four jhānas *Arūpajhāna, Four arūpajhānas *Brahmavihara, Four Divine Abidings – Mettā, loving-kindness, Karuṇā, compassion, Mudita, sympathetic joy, and Upekkha, equanimity *Four stages of enlightenment – Sotāpanna, stream-enterer, Sakadagami, once-returner, Anagami, non-returner, and Arahant (Buddhism), arahant *Buddhist pilgrimage, Four main pilgrimage sites – Lumbini, Bodh Gaya, Sarnath, and KusinaraJudeo-Christian symbolism
*The Tetragrammaton is the four-letter name of God. *Ezekiel has a vision of four living creatures (Bible), living creatures: a man, a lion, an ox, and an eagle. *The four Matriarchs (foremothers) of Judaism are Sarah, Rebekah, Leah, and Rachel. *The Four Species (lulav, hadass, Aravah (Sukkot), aravah and etrog) are taken as one of the mitzvah, mitzvot on the Jewish holiday of Sukkot. (Judaism) *The Four Cups of Wine to drink on the Jewish holiday of Passover. (Judaism) *The Four Questions to be asked on the Jewish holiday of Passover. (Judaism) *The Four Sons to be dealt with on the Jewish holiday of Passover. (Judaism) *The Four Expressions of Redemption to be said on the Jewish holiday of Passover. (Judaism) *The four Gospels: Gospel of Matthew, Matthew, Gospel of Mark, Mark, Gospel of Luke, Luke, and Gospel of John, John. (Christianity) *The Four Horsemen of the Apocalypse ride in the Book of Revelation. (Christianity) *The Holy cities of Judaism, four holy cities of Judaism: Jerusalem, Hebron, Safed, and Tiberias, TiberiusHinduism
*There are four Vedas: Rigveda, Samaveda, Yajurveda and Atharvaveda. *In Puruṣārtha, there are four aims of human life: Dharma, Artha, Kāma, Moksha. *The four stages of life Brahmacharya (student life), Grihastha (household life), Vanaprastha (retired life) and Sannyasa (renunciation). *The four primary castes or strata of society: Brahmana (priest/teacher), Kshatriya (warrior/politician), Vaishya (landowner/entrepreneur) and Shudra (servant/manual laborer). *The swastika symbol is traditionally used in Hindu religions as a sign of good luck and signifies good from all four directions. *The god Brahma has four faces. *There are four ''yugas'': ''Satya Yuga, Satya'', ''Dvapara Yuga, Dvapara'', ''Treta Yuga, Treta'' and ''Kali Yuga, Kali''Islam
*Eid al-Adha lasts for four days, from the 10th to the 14th of Dhul Hijja. *The Holiest sites in Islam, four holy cities of Islam: Mecca, Medina, Jerusalem and Damascus. *The Green Dome, four tombs in the Green Dome: Muhammad, Abu Bakr, Umar ibn Khattab and Isa ibn Maryam (Jesus). *There are four Rashidun or Rightly Guided Caliphs: Abu Bakr, Umar ibn al-Khattab, Uthman ibn Affan and Ali ibn Abi Talib. *The Four Archangel#In Islam, Arch Angels in Islam are: Jibraeel (Gabriel), Mikaeel (Michael), Izraeel (Azrael), and Israfil (Raphael) *There are four months in which war is not permitted: Muharram, Rajab, Dhu al-Qi'dah and Dhu al-Hijjah. *There are four Sunni schools of fiqh: Hanafi, Shafi`i, Maliki and Hanbali. *There are four major Sunni Imams: Abū Ḥanīfa, Muhammad ibn Idris ash-Shafi`i, Malik ibn Anas and Ahmad ibn Hanbal. *There are four Islamic holy books, books in Islam: Taurait, Zaboor, Injeel, Quran. *Waiting for four months is ordained for those who take an oath for abstention from their wives. *The waiting period of the woman whose husband dies is Islamic funeral#Directives for widows, four months and ten days. *When Abraham said: "My Lord, show me how You give life to the dead," Allah said: "Why! Do you have no faith?" Abraham replied: "Yes, but in order that my heart be at rest." He said: "Then take four birds, and tame them to yourself, then put a part of them on every hill, and summon them; they will come to you flying. [Al-Baqara 2:260] *The respite of four months was granted to give time to the mushriks in Surah At-Tawba so that they should consider their position carefully and decide whether to make preparation for war or to emigrate from the country or to accept Islam. *Those who accuse honorable women (of unchastity) but do not produce four witnesses, flog them with eighty lashes, and do not admit their testimony ever after. They are indeed transgressors. [An-Noor 24:4]Taoism
*Four Symbols of I ChingOther
*In a more general sense, numerous mythological and cosmogonical systems consider Four corners of the world as essentially corresponding to the four points of the compass. *Four is the sacred number of the Zia (New Mexico), Zia, an indigenous tribe located in the U.S. state of New Mexico. *The Chinese, the Koreans, and the Japanese are tetraphobia, superstitious about the number four because it is a homonym for "death" in their languages. *In Slavic mythology, the god Svetovid has four heads.In politics
*Four Freedoms: four fundamental freedoms that Franklin D. Roosevelt declared ought to be enjoyed by everyone in the world: Freedom of Speech, Freedom of Religion, Freedom from Want, Freedom from Fear. *Gang of Four: Popular name for four Chinese Communist Party leaders who rose to prominence during China's Cultural Revolution, but were ousted in 1976 following the death of Chairman Mao Zedong. Among the four was Mao's widow, Jiang Qing. Since then, many other political factions headed by four people have been called "Gangs of Four".In computing
*Four bits (half a byte) are sometimes called a nibble.In science
*A tetramer is an oligomer formed out of four sub-units.In astronomy
*Four terrestrial (or rocky) planets in the Solar System: Mercury (planet), Mercury, Venus, Earth, and Mars. *Four giant gas/ice planets in the Solar System: Jupiter, Saturn, Uranus, and Neptune. *Four of Jupiter's moons (the Galilean moons) are readily visible from Earth with a hobby telescope. *Messier object Messier 4, M4, a magnitude 7.5 globular cluster in the constellation Scorpius. *The Roman numeral IV stands for subgiant in the stellar classification, Yerkes spectral classification scheme.In biology
*Four is the number of nucleobase types in DNA and RNA – adenine, guanine, cytosine, thymine (uracil in RNA). *Many chordates have four feet, legs or leglike appendages (tetrapods). *The mammalian heart consists of four chambers. *Many mammals (Carnivora, Ungulata) use four fingers for movement. *All insects with wings except fly, flies and some others have four wings. *Insects of the superorder Endopterygota, also known as Holometabola, such as butterflies, ants, bees, beetles, fleas, flies, moths, and wasps, undergo holometabolism—complete metamorphism in four stages—from (1) embryo (ovum, egg), to (2) larva (such as grub, caterpillar), then (3) pupa (such as the chrysalis), and finally (4) the imago. *In the common ABO blood group system, there are four blood types (A, B, O, AB). *Humans have four canine tooth, canines and four wisdom teeth. *The cow's stomach is divided in four digestive compartments: reticulum, rumen, omasum and abomasum.In chemistry
*Valence (chemistry), Valency of carbon (that is basis of life on the Earth) is four. Also because of its tetrahedral crystal bond structure, diamond (one of the natural allotropes of carbon) is the hardest known naturally occurring material. It is also the valence of silicon, whose compounds form the majority of the mass of the Earth's crust. *The atomic number of beryllium *There are four basic states of matter: solid, liquid, gas, and plasma (physics), plasma.In physics
*Special relativity and general relativity treat nature as four-dimensional: Three-dimensional space (mathematics), 3D regular space and one-dimensional time are treated together and called spacetime. Also, any event ''E'' has a light cone composed of four zones of possible communication and cause and effect (outside the light cone is strictly incommunicado). *There are four fundamental forces (electromagnetism, gravitation, the weak nuclear force, and the strong nuclear force). *In statistical mechanics, the four functions inequality is an inequality for four functions on a finite distributive lattice.In logic and philosophy
 *The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The Square of Opposition, in both its Aristotelian version and its Square of Opposition#Modern squares of opposition, Boolean version, consists of four forms: A ("All ''S'' is ''R''"), I ("Some ''S'' is ''R''"), E ("No ''S'' is ''R''"), and O ("Some ''S'' is not ''R''").
*In regard to whether two given propositions can have the same truth value, there are four separate logical possibilities: the propositions are ''subalterns'' (possibly both are true, and possibly both are false); ''subcontraries'' (both may be true, but not that both are false); ''contraries'' (both may be false, but not that both are true); or ''contradictories'' (it is not possible that both are true, and it is not possible that both are false).
*Aristotle held that there are basically four causes in nature: the Four causes#Material cause, material, the Four causes#Formal cause, formal, the Four causes#Efficient cause, efficient, and the Four causes#Final cause, final.
*The Stoicism, Stoics held with four basic categories (Stoic), categories, all viewed as bodies (substantial and insubstantial): (1) ''substance'' in the sense of substrate, primary formless matter; (2) ''quality'', matter's organization to differentiate and individualize something, and coming down to a physical ingredient such as ''pneuma'', breath; (3) ''somehow holding'' (or ''disposed''), as in a posture, state, shape, size, action, and (4) ''somehow holding'' (or ''disposed'') ''toward something,'' as in relative location, familial relation, and so forth.
*Immanuel Kant expounded a Category (Kant)#The table of judgments, table of judgments involving four three-way alternatives, in regard to (1) Quantity, (2) Quality, (3) Relation, (4) Modality, and, based thereupon, a Category (Kant)#The table of categories, table of four categories, named by the terms just listed, and each with three subcategories.
*Arthur Schopenhauer's doctoral thesis was ''On the Fourfold Root of the Principle of Sufficient Reason''.
*Franz Brentano held that any major philosophical period has four phases: (1) Creative and rapidly progressing with scientific interest and results; then declining through the remaining phases, (2) practical, (3) increasingly skeptical, and (4) literary, mystical, and scientifically worthless—until philosophy is renewed through a new period's first phase. (See Brentano's essay "The Four Phases of Philosophy and Its Current State" 1895, tr. by Mezei and Smith 1998.)
*Charles Sanders Peirce, C. S. Peirce, usually a trichotomy (philosophy), trichotomist, discussed four methods for overcoming troublesome uncertainties and achieving secure beliefs: (1) the method of tenacity (policy of sticking to initial belief), (2) the method of authority, (3) the method of congruity (following a fashionable paradigm), and (4) the Fallibilism, fallibilistic, self-correcting method of science (see "s:The Fixation of Belief, The Fixation of Belief", 1877); and four barriers to inquiry, barriers refused by the fallibilist: (1) assertion of absolute certainty; (2) maintaining that something is unknowable; (3) maintaining that something is inexplicable because absolutely basic or ultimate; (4) holding that perfect exactitude is possible, especially such as to quite preclude unusual and anomalous phenomena (see
*The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The Square of Opposition, in both its Aristotelian version and its Square of Opposition#Modern squares of opposition, Boolean version, consists of four forms: A ("All ''S'' is ''R''"), I ("Some ''S'' is ''R''"), E ("No ''S'' is ''R''"), and O ("Some ''S'' is not ''R''").
*In regard to whether two given propositions can have the same truth value, there are four separate logical possibilities: the propositions are ''subalterns'' (possibly both are true, and possibly both are false); ''subcontraries'' (both may be true, but not that both are false); ''contraries'' (both may be false, but not that both are true); or ''contradictories'' (it is not possible that both are true, and it is not possible that both are false).
*Aristotle held that there are basically four causes in nature: the Four causes#Material cause, material, the Four causes#Formal cause, formal, the Four causes#Efficient cause, efficient, and the Four causes#Final cause, final.
*The Stoicism, Stoics held with four basic categories (Stoic), categories, all viewed as bodies (substantial and insubstantial): (1) ''substance'' in the sense of substrate, primary formless matter; (2) ''quality'', matter's organization to differentiate and individualize something, and coming down to a physical ingredient such as ''pneuma'', breath; (3) ''somehow holding'' (or ''disposed''), as in a posture, state, shape, size, action, and (4) ''somehow holding'' (or ''disposed'') ''toward something,'' as in relative location, familial relation, and so forth.
*Immanuel Kant expounded a Category (Kant)#The table of judgments, table of judgments involving four three-way alternatives, in regard to (1) Quantity, (2) Quality, (3) Relation, (4) Modality, and, based thereupon, a Category (Kant)#The table of categories, table of four categories, named by the terms just listed, and each with three subcategories.
*Arthur Schopenhauer's doctoral thesis was ''On the Fourfold Root of the Principle of Sufficient Reason''.
*Franz Brentano held that any major philosophical period has four phases: (1) Creative and rapidly progressing with scientific interest and results; then declining through the remaining phases, (2) practical, (3) increasingly skeptical, and (4) literary, mystical, and scientifically worthless—until philosophy is renewed through a new period's first phase. (See Brentano's essay "The Four Phases of Philosophy and Its Current State" 1895, tr. by Mezei and Smith 1998.)
*Charles Sanders Peirce, C. S. Peirce, usually a trichotomy (philosophy), trichotomist, discussed four methods for overcoming troublesome uncertainties and achieving secure beliefs: (1) the method of tenacity (policy of sticking to initial belief), (2) the method of authority, (3) the method of congruity (following a fashionable paradigm), and (4) the Fallibilism, fallibilistic, self-correcting method of science (see "s:The Fixation of Belief, The Fixation of Belief", 1877); and four barriers to inquiry, barriers refused by the fallibilist: (1) assertion of absolute certainty; (2) maintaining that something is unknowable; (3) maintaining that something is inexplicable because absolutely basic or ultimate; (4) holding that perfect exactitude is possible, especially such as to quite preclude unusual and anomalous phenomena (seeF.R.L.
[First Rule of Logic], 1899). *Paul Weiss (philosopher), Paul Weiss built a system involving four modes of being: Actualities (substances in the sense of substantial, spatiotemporally finite beings), Ideality or Possibility (pure normative form), Existence (the dynamic field), and God (unity). (See Weiss's ''Modes of Being'', 1958). *Karl Popper outlined a tetradic schema to describe the growth of theories and, via generalization, also the emergence of new behaviors and living organisms: (1) problem, (2) tentative theory, (3) (attempted) error-elimination (especially by way of critical discussion), and (4) new problem(s). (See Popper's ''Objective Knowledge'', 1972, revised 1979.) *John Boyd (military strategist) made his key concept the decision cycle or John Boyd (military strategist)#OODA loop, OODA loop, consisting of four stages: (1) observation (data intake through the senses), (2) orientation (analysis and synthesis of data), (3) decision, and (4) action. Boyd held that his decision cycle has philosophical generality, though for strategists the point remains that, through swift decisions, one can disrupt an opponent's decision cycle. *Richard McKeon outlined four classes (each with four subclasses) of modes of philosophical inquiry: (1) Modes of Being (Being); (2) Modes of Thought (That which is); (3) Modes of Fact (Existence); (4) Modes of Simplicity (Experience)—and, corresponding to them, four classes (each with four subclasses) of philosophical semantics: Principles, Methods, Interpretations, and Selections. (See McKeon's "Philosophic Semantics and Philosophic Inquiry" in ''Freedom and History and Other Essays'', 1989.) *Jonathan Lowe (E.J. Lowe) argues in ''The Four-Category Ontology'', 2006, for four categories: ''kinds'' (substantial universals), ''attributes'' (relational universals and property-universals), ''objects'' (substantial particulars), and ''modes'' (relational particulars and property-particulars, also known as "trope (philosophy), tropes"). (See Lowe's "Recent Advances in Metaphysics," 2001
Eprint
*Four opposed camps of the morality and nature of evil: moral absolutism, amoralism, moral relativism, and moral universalism.
In technology
rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s (with four angles and four sides) because they have effective form and capability for close adjacency to each other (houses, rooms, tables, bricks, sheets of paper, screens, film frames).
*In the Rich Text Format specification, language code 4 is for the Chinese language. Codes for regional variants of Chinese are congruent to .
*Credit card machines have four-twelve function keys.
*On most phones, the 4 key is associated with the letters G, H, and I, but on the BlackBerry Pearl, it is the key for D and F.
*On many computer keyboards, the "4" key may also be used to type the dollar sign ($) if the shift key is held down.
*It is the number of bits in a nibble, equivalent to half a byte
*In internet slang, "4" can replace the word "for" (as "four" and "for" are pronounced similarly). For example, typing "4u" instead of "for you".
*In Leetspeak, "4" may be used to replace the letter "A".
*The Internet protocol suite, TCP/IP stack consists of four layers.
In transport
In sports
* In the Australian Football League, the top level of Australian rules football, each team is allowed 4 "Interchange (Australian rules football), interchanges" (substitute players), who can be freely substituted at any time, subject to a limit on the total number of substitutions. *In baseball: **There are four bases in the game: first base, second base, third base, and home plate; to score a run, an offensive player must complete, in the sequence shown, a circuit of those four bases. ** When a batter receives four pitches that the umpire declares to be "Strike zone, balls" in a single at-bat, a base on balls, informally known as a "walk", is awarded, with the batter sent to first base. **For scoring, number 4 is assigned to the second baseman. **Four is the most runs that can be scored on any single at bat, whereby all three baserunners and the batter score (the most common being via a grand slam (baseball), grand slam). **The fourth batter in the batting lineup is called the cleanup hitter. *In basketball, the number four is used to designate the Power forward (basketball), power forward position, often referred to as "the four spot" or "the four". *In cricket, a four is a specific type of scoring event, whereby the ball crosses the boundary (cricket), boundary after touching the ground at least one time, scoring four runs. Taking four wickets in four consecutive balls is typically referred to as a double hat trick (two consecutive, overlapping hat tricks). *In American Football teams get four downs to reach the line of gain. *In rowing (sport), rowing, a four refers to a boat for four rowers, with or without coxswain. In rowing nomenclature, 4− represents a coxless four and 4+ represents a coxed four. *In rugby league: ** A Try (rugby), try is worth 4 points. ** One of the two starting centres wears the jersey number 4. (An exception to this rule is the Super League, which uses static squad numbering.) *In rugby union: ** One of the two starting Lock (rugby union), locks wears the jersey number 4. ** In the standard Rugby union bonus points system, bonus points system, a point is awarded in the league standings to a team that scores at least 4 tries in a match, regardless of the match result.In other fields
In music
*In written music, Time signature, common time is constructed of four beats per measure and a quarter note receives one beat. *In popular or Popular music, modern music, the most common time signature is also founded on four beats, i.e., 4/4 having four quarter note beats. *The common major scale is built on two sets of four notes (e.g., CDEF, GABC), where the first and last notes create an octave interval (a pair-of-four relationship). *The interval of a perfect fourth is a foundational element of many genres of music, represented in music theory as the tonic (music), tonic and subdominant relationship. Four is also embodied within the circle of fifths (also known as circle of fourths), which reveals the interval of four in more active harmonic contexts. *The typical number of movements in a symphony. *The number of completed, numbered symphonies by Johannes Brahms. *The number of strings on a violin, a viola, a cello, double bass, a cuatro (instrument), cuatro, a typical bass guitar, and a ukulele, and the number of string pairs on a mandolin. *"Four calling birds" is the gift on the fourth day of Christmas in the carol "The Twelve Days of Christmas (song), The Twelve Days of Christmas".Groups of four
* Big Four (disambiguation) *Four basic operations of arithmetic:addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
, subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
, multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
, division (mathematics), division.
*Classical element#Classical elements in Greece, Greek classical elements (fire, air, water, earth).
*Season, Four seasons: spring (season), spring, summer, autumn, winter.
*The Four Seasons (disambiguation)
*A leap year generally occurs every four years.
*Approximately four weeks (4 times 7 days) to a lunar month (synodic month = 29.53 days). Thus the number four is universally an integral part of primitive sacred calendars.
*Four weeks of Advent (and four Advent candles on the Advent wreath).
*Four cardinal directions: north, south, east, west.
*Four Temperaments: sanguine, choleric, Melancholia, melancholic, phlegmatic.
*Humorism, Four Humors: blood, yellow bile, black bile, phlegm.
*Four Great Ancient Capitals of China.
*Four-corner method.
*Four Asian Tigers, referring to the economies of Hong Kong, Taiwan, South Korea, and Singapore
*Four cardinal principles, Cardinal principles.
*Four cardinal virtues: justice, prudence, temperance, fortitude.
*Four suit (cards), suits of playing cards: hearts, diamonds, clubs, spades.
*Four nations of the United Kingdom: England, Wales, Scotland, Northern Ireland.
*Four provinces of Ireland: Munster, Ulster, Leinster, Connacht.
*Four estates: politics, public administration, administration, judiciary, journalism. Especially in the expression "Fourth Estate", which means journalism.
*Four Corners Monument, Four Corners is the only location in the United States where four U.S. state, states come together at a single point: Colorado, Utah, New Mexico, and Arizona.
* Four Evangelists – Matthew the Apostle, Matthew, Mark the Evangelist, Mark, Luke the Evangelist, Luke, and John the Evangelist, John
* Four Doctor of the Church, Doctors of Western Church – Saint Gregory the Great, Saint Ambrose, Saint Augustine, and Saint Jerome
* Four Doctors of Eastern Church – Saint John Chrysostom, Saint Basil the Great, and Gregory of Nazianzus and Saint Athanasius
* Four Galilean moons of Jupiter – Io (moon), Io, Europa (moon), Europa, Ganymede (moon), Ganymede, and Callisto (moon), Callisto
* The Gang of Four was a Communist Party of China, Chinese communist political faction.
* The Fantastic Four: Mr. Fantastic, The Invisible Woman, The Human Torch, The Thing.
* The Teenage Mutant Ninja Turtles: Leonardo, Michelangelo, Donatello, Raphael
* The Beatles were also known as the "Fab Four": John Lennon, Paul McCartney, George Harrison, Ringo Starr.
* Gang of Four (band), Gang of Four is a British post-punk rock and roll, rock band formed in the late 1970s.
* Four rivers in the Garden of Eden (Book of Genesis, Genesis 2:10–14): Pishon (perhaps the Jaxartes or Syr Darya), Gihon (perhaps the Oxus or Amu Darya), Hiddekel (Tigris), and P'rat (Euphrates).
* There are also four years in a single Olympiad (duration between the Olympic Games). Many major international sports competitions follow this cycle, among them the FIFA World Cup and its FIFA Women's World Cup, women's version, the FIBA World Championships for FIBA World Championship, men and FIBA World Championship for Women, women, and the Rugby World Cup.
* There are four limbs on the human body.
* Four Houses of Hogwarts in the Harry Potter series: Gryffindor, Hufflepuff, Ravenclaw, Slytherin.
* Four known continents of the world in the ''A Song of Ice and Fire'' series: Westeros, Essos, Sothoryos, Ulthos.
* Each Grand Prix in Nintendo's ''Mario Kart'' series is divided into four cups and each cup is divided into four courses. The Mushroom Cup, Flower Cup, Star Cup, and Special Cup make up the Nitro Grand Prix, while the Shell Cup, Banana Cup, Leaf Cup, and the Lightning Cup make up the Retro Grand Prix.
See also
*List of highways numbered 4References
*Wells, D. ''The Penguin Dictionary of Curious and Interesting Numbers'' London: Penguin Group. (1987): 55–58External links
Marijn.Org on Why is everything four?
by Penelope Merritt at samuel-beckett.net
The Number 4
{{Authority control Integers 4 (number),