2005 Bougainvillean General Election on:
[Wikipedia]
[Google]
[Amazon]
5 (five) is a
 is the third smallest
is the third smallest
 A pentagram, or five-pointed Polygram (geometry), polygram, is the first proper star polygon constructed from the diagonals of a
A pentagram, or five-pointed Polygram (geometry), polygram, is the first proper star polygon constructed from the diagonals of a
"Cubic Symmetric Graphs (The Foster Census)."
The automorphism group of the Petersen graph is the symmetric group of group order, order 120 (number), 120 = 5!. The Hadwiger–Nelson problem, chromatic number of the plane is at least five, depending on the choice of Axiom of choice, set-theoretical axioms: the minimum number of Graph coloring, colors required to color the plane such that no pair of points at a distance of 1 has the same color. Whereas the hexagonal Golomb graph and the regular hexagonal tiling generate chromatic numbers of 4 and 7, respectively, a chromatic coloring of 5 can be attained under a more complicated graph where multiple four-coloring Moser spindles are linked so that no monochromatic triples exist in any coloring of the overall graph, as that would generate an equilateral arrangement that tends toward a purely hexagonal Structure (mathematical logic), structure. The Plane (geometry), plane contains a total of five Bravais lattices, or arrays of Point (geometry), points defined by discrete Translation (geometry), translation operations: Hexagonal lattice, hexagonal, Oblique lattice, oblique, Rectangular lattice, rectangular, Rectangular lattice#Bravais lattices, centered rectangular, and Square lattice, square lattices. The plane can also be tiled Pentagonal tiling#Monohedral convex pentagonal tilings, monohedrally with convex pentagonal tiling, pentagons in fifteen different ways, three of which have Laves tilings as special cases. Five points are needed to determine a conic section, in the Five points determine a conic, same way that two points are needed to determine a line. A Veronese surface in the Projective space, projective plane of a conic generalizes a Pairing, linear condition for a point to be contained inside a conic.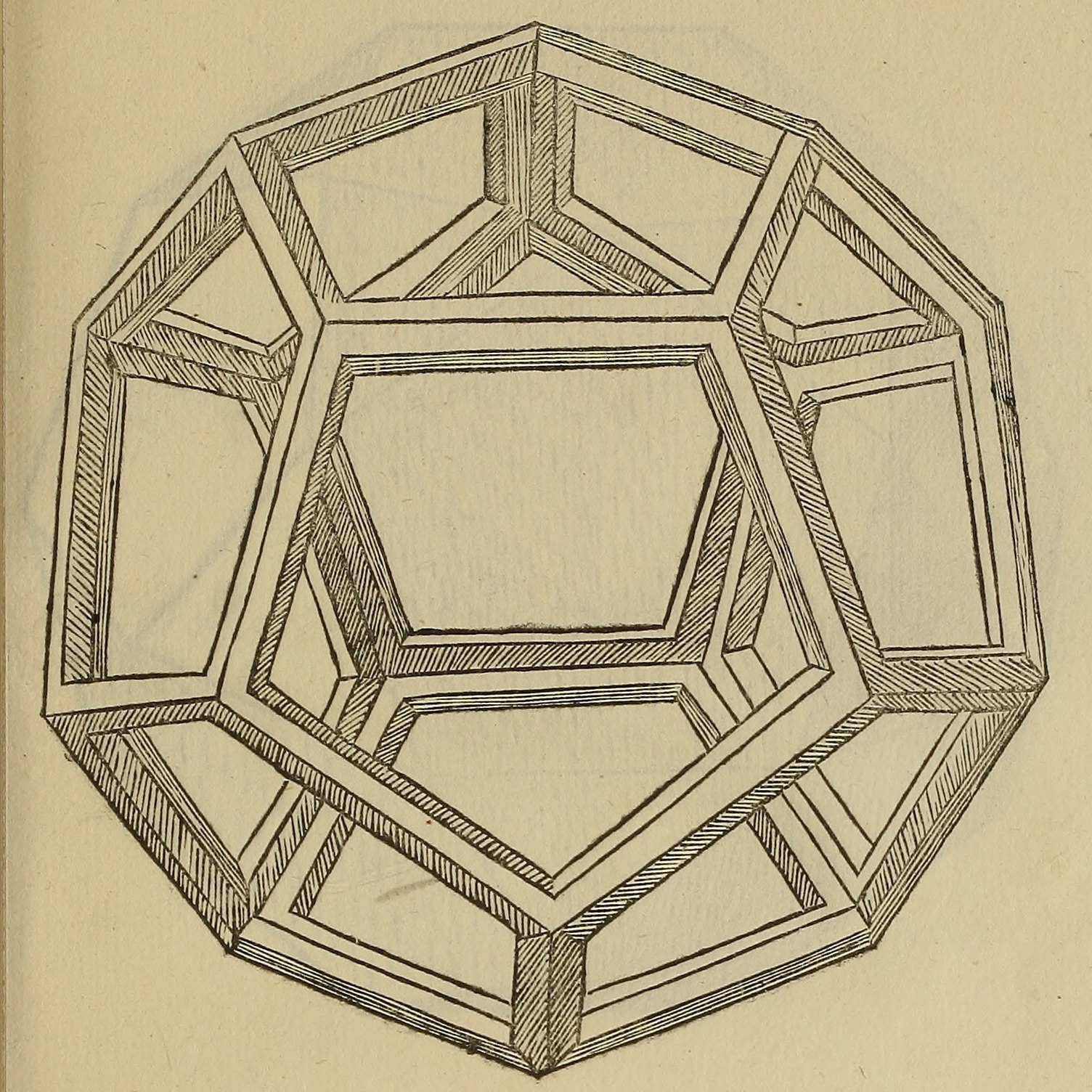 There are Platonic solid, Platonic solids in three-dimensional space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The Regular dodecahedron, dodecahedron in particular contains pentagonal faces, while the Regular icosahedron, icosahedron, its Dual polytope, dual polyhedron, has a vertex figure that is a regular pentagon. There are also :
☆ Uniform polyhedron compound, Regular polyhedron compounds: the stella octangula, compound of five tetrahedra, compound of five cubes, compound of five octahedra, and compound of ten tetrahedra. Icosahedral symmetry is isomorphic to the alternating group on 5 letters of order 120 (number), 120, realized by actions on these uniform polyhedron compounds.
☆ Honeycomb (geometry), Space-filling convex polyhedron, convex polyhedra: the triangular prism, hexagonal prism, cube, truncated octahedron, and gyrobifastigium. While the cube is the only Platonic solid that can tessellate space on its own, the truncated octahedron and the gyrobifastigium are the only Archimedean solid, Archimedean and Johnson solids, respectively, that can also tessellate space with their own copies.
☆ Isohedral figure#Related terms, Cell-transitive Parallelohedron, parallelohedra: any parallelepiped, as well as the rhombic dodecahedron and elongated dodecahedron, and the hexagonal prism and truncated octahedron. The cube is a special case of a parallelepiped, with the rhombic dodecahedron the only Catalan solid to tessellate space on its own.
☆ List of regular polytopes and compounds#Abstract polytopes, Regular abstract polyhedra, which include the excavated dodecahedron and the dodecadodecahedron. They have combinatorial symmetries transitive on List of regular polytopes and compounds#Abstract polytopes, flags of their elements, with Topology, topologies equivalent to that of toroids and the ability to tile the hyperbolic plane.
The 5-cell, or pentatope, is the self-dual fourth-dimensional analogue of the tetrahedron, with Coxeter group symmetry of order 120 (number), 120 = 5Factorial, ! and Mathematical structure, group structure. Made of five tetrahedra, its Petrie polygon is a
There are Platonic solid, Platonic solids in three-dimensional space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The Regular dodecahedron, dodecahedron in particular contains pentagonal faces, while the Regular icosahedron, icosahedron, its Dual polytope, dual polyhedron, has a vertex figure that is a regular pentagon. There are also :
☆ Uniform polyhedron compound, Regular polyhedron compounds: the stella octangula, compound of five tetrahedra, compound of five cubes, compound of five octahedra, and compound of ten tetrahedra. Icosahedral symmetry is isomorphic to the alternating group on 5 letters of order 120 (number), 120, realized by actions on these uniform polyhedron compounds.
☆ Honeycomb (geometry), Space-filling convex polyhedron, convex polyhedra: the triangular prism, hexagonal prism, cube, truncated octahedron, and gyrobifastigium. While the cube is the only Platonic solid that can tessellate space on its own, the truncated octahedron and the gyrobifastigium are the only Archimedean solid, Archimedean and Johnson solids, respectively, that can also tessellate space with their own copies.
☆ Isohedral figure#Related terms, Cell-transitive Parallelohedron, parallelohedra: any parallelepiped, as well as the rhombic dodecahedron and elongated dodecahedron, and the hexagonal prism and truncated octahedron. The cube is a special case of a parallelepiped, with the rhombic dodecahedron the only Catalan solid to tessellate space on its own.
☆ List of regular polytopes and compounds#Abstract polytopes, Regular abstract polyhedra, which include the excavated dodecahedron and the dodecadodecahedron. They have combinatorial symmetries transitive on List of regular polytopes and compounds#Abstract polytopes, flags of their elements, with Topology, topologies equivalent to that of toroids and the ability to tile the hyperbolic plane.
The 5-cell, or pentatope, is the self-dual fourth-dimensional analogue of the tetrahedron, with Coxeter group symmetry of order 120 (number), 120 = 5Factorial, ! and Mathematical structure, group structure. Made of five tetrahedra, its Petrie polygon is a

 The evolution of the modern Western digit for the numeral 5 cannot be traced back to the Brahmi numerals, Indian system, as for the digits 1 to 4. The Kushan Empire, Kushana and Gupta Empire, Gupta empires in what is now India had among themselves several different forms that bear no resemblance to the modern digit. The Devanagari, Nagari and Punjabi language, Punjabi took these digits and all came up with forms that were similar to a lowercase "h" rotated 180°. The Ghubar Arabs transformed the digit in several different ways, producing from that were more similar to the digits 4 or 3 than to 5. It was from those digits that Europeans finally came up with the modern 5.
While the shape of the character for the digit 5 has an Ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in .
On the seven-segment display of a calculator, it is represented by five segments at four successive turns from top to bottom, rotating counterclockwise first, then clockwise, and vice-versa.
The evolution of the modern Western digit for the numeral 5 cannot be traced back to the Brahmi numerals, Indian system, as for the digits 1 to 4. The Kushan Empire, Kushana and Gupta Empire, Gupta empires in what is now India had among themselves several different forms that bear no resemblance to the modern digit. The Devanagari, Nagari and Punjabi language, Punjabi took these digits and all came up with forms that were similar to a lowercase "h" rotated 180°. The Ghubar Arabs transformed the digit in several different ways, producing from that were more similar to the digits 4 or 3 than to 5. It was from those digits that Europeans finally came up with the modern 5.
While the shape of the character for the digit 5 has an Ascender (typography), ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in .
On the seven-segment display of a calculator, it is represented by five segments at four successive turns from top to bottom, rotating counterclockwise first, then clockwise, and vice-versa.
object
NGC 5, a apparent magnitude, magnitude 13 spiral galaxy in the constellation Andromeda (constellation), Andromeda. *The Roman numeral V stands for dwarfs (main sequence stars) in the stellar classification, Yerkes spectral classification scheme. *The Roman numeral V (usually) stands for the fifth-discovered satellite of a planet or minor planet (e.g. Amalthea (moon), Jupiter V). *There are five Lagrangian points in a two-body system.
The Number 5The Positive Integer 5
{{DEFAULTSORT:5 (Number) Integers 5 (number)
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
, numeral and digit. It is the natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
, and cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. Th ...
, following 4 and preceding 6, and is a prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. It has attained significance throughout history in part because typical humans have five digits on each hand.
In mathematics
prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
, and the second super-prime
Super-prime numbers, also known as higher-order primes or prime-indexed primes (PIPs), are the subsequence of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers.
The subsequence begins
:3, 5, 11, 17, 31, ...
. It is the first safe prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + ...
, the first good prime A good prime is a prime number whose square is greater than the product of any two primes at the same number of positions before and after it in the sequence of primes.
That is, good prime satisfies the inequality
:p_n^2 > p_ \cdot p_
for all 1 � ...
, the first balanced prime In number theory, a balanced prime is a prime number with equal-sized prime gaps above and below it, so that it is equal to the arithmetic mean of the nearest primes above and below. Or to put it algebraically, given a prime number p_n, where is it ...
, and the first of three known Wilson prime
In number theory, a Wilson prime is a prime number p such that p^2 divides (p-1)!+1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides (p-1)!+1. Both are named for 18th-century E ...
s. Five is the second Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
and the third Mersenne prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17t ...
exponent, as well as the third Catalan number
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Cata ...
, and the third Sophie Germain prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + ...
. Notably, 5 is equal to the sum of the ''only'' consecutive primes, 2 + 3, and is the only number that is part of more than one pair of twin prime
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term ''twin pr ...
s, ( 3, 5) and (5, 7). It is also a sexy prime
In number theory, sexy primes are prime numbers that differ from each other by 6. For example, the numbers 5 and 11 are both sexy primes, because both are prime and .
The term "sexy prime" is a pun stemming from the Latin word for six: .
If o ...
with the fifth prime number and first prime repunit, 11. Five is the third factorial prime
A factorial prime is a prime number that is one less or one more than a factorial (all factorials greater than 1 are even).
The first 10 factorial primes (for ''n'' = 1, 2, 3, 4, 6, 7, 11, 12, 14) are :
: 2 (0! +&n ...
, an alternating factorial, and an Eisenstein prime
In mathematics, an Eisenstein prime is an Eisenstein integer
: z = a + b\,\omega, \quad \text \quad \omega = e^,
that is irreducible (or equivalently prime) in the ring-theoretic sense: its only Eisenstein divisors are the units , itself ...
with no imaginary part and real part of the form − . In particular, five is the first congruent number
In number theory, a congruent number is a positive integer that is the area of a right triangle with three rational number sides. A more general definition includes all positive rational numbers with this property.
The sequence of (integer) cong ...
, since it is the length of the hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equa ...
of the smallest integer-sided right triangle.
Five is the second Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
of the form + , and more generally the second Sierpiński number of the first kind, + . There are a total of five known Fermat primes, which also include 3, 17, 257, and 65537
65537 is the integer after 65536 and before 65538.
In mathematics
65537 is the largest known prime number of the form 2^ +1 (n = 4). Therefore, a regular polygon with 65537 sides is constructible with compass and unmarked straightedge. Johann ...
. The sum of the first 3 Fermat primes, 3, 5 and 17, yields 25 or 52, while 257 is the 55th prime number. Combinations from these 5 Fermat primes generate 31 polygons with an odd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
number of sides that can be construncted purely with a compass and straight-edge, which includes the five-sided regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
. Apropos, 31 is also equal to the sum of the maximum number of area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
s inside a circle that are formed from the sides and diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek δ ...
s of the first five -sided polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two toge ...
s, and equal to the maximum number of areas formed by a six-sided polygon; per Moser's circle problem.
The number 5 is the fifth Fibonacci number
In mathematics, the Fibonacci numbers, commonly denoted , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from ...
, being 2 plus 3. It is the only Fibonacci number that is equal to its position aside from 1, which is both the first and second Fibonacci numbers. Five is also a Pell number
In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins , , , , an ...
and a Markov number
A Markov number or Markoff number is a positive integer ''x'', ''y'' or ''z'' that is part of a solution to the Markov Diophantine equation
:x^2 + y^2 + z^2 = 3xyz,\,
studied by .
The first few Markov numbers are
: 1, 2, 5, 13, 29, 34, 89 ...
, appearing in solutions to the Markov Diophantine equation: (1, 2, 5), (1, 5, 13), (2, 5, 29), (5, 13, 194), (5, 29, 433), ... ( lists Markov numbers that appear in solutions where one of the other two terms is 5). Whereas 5 is unique in the Fibonacci sequence, in the Perrin sequence 5 is both the fifth and sixth Perrin number
In mathematics, the Perrin numbers are defined by the recurrence relation
: for ,
with initial values
:.
The sequence of Perrin numbers starts with
: 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, ...
The number of different maxima ...
s.
5 is the third Mersenne prime exponent of the form − , which yields : the prime index of the third Mersenne prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17t ...
and second double Mersenne prime
In mathematics, a double Mersenne number is a Mersenne number of the form
:M_ = 2^-1
where ''p'' is prime.
Examples
The first four terms of the sequence of double Mersenne numbers areChris Caldwell''Mersenne Primes: History, Theorems and Li ...
127, as well as the third double Mersenne prime exponent for the number 2,147,483,647
The number 2,147,483,647 is the eighth Mersenne prime, equal to 231 − 1. It is one of only four known double Mersenne primes.
The primality of this number was proven by Leonhard Euler, who reported the proof in a letter to Daniel ...
, which is the largest value that a signed 32-bit
In computer architecture, 32-bit computing refers to computer systems with a processor, memory, and other major system components that operate on data in 32-bit units. Compared to smaller bit widths, 32-bit computers can perform large calculation ...
integer field can hold. There are only four known double Mersenne prime numbers, with a fifth candidate double Mersenne prime = 223058...93951 − 1 too large to compute with current computers. In a related sequence, the first 5 terms in the sequence of Catalan–Mersenne numbers are the only known prime terms, with a sixth possible candidate in the order of 101037.7094. These prime sequences are conjectured to be prime up to a certain limit.
Every odd number greater than is the sum of at most five prime numbers, and every odd number greater than is conjectured to be expressible as the sum of three prime numbers. Helfgtott has provided a proof of the latter, also known as the odd Goldbach conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that
: Every odd number greater than 5 can be expressed as the sum of three prime number, prime ...
, that is already widely acknowledged by mathematicians as it still undergoes peer-review
Peer review is the evaluation of work by one or more people with similar competencies as the producers of the work (peers). It functions as a form of self-regulation by qualified members of a profession within the relevant field. Peer review ...
.
The sums of the first five non-primes greater than zero + + + + and the first five prime numbers + + + + both equal ; the 7th triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
and like a perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
, which also includes , the 31st triangular number and perfect number of the form −1( − ) with a of , by the Euclid–Euler theorem
The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form , where is a prime number. The theorem is named after mathematician ...
.
There are a total of five known unitary perfect number
A unitary perfect number is an integer which is the sum of its positive proper unitary divisors, not including the number itself (a divisor ''d'' of a number ''n'' is a unitary divisor if ''d'' and ''n''/''d'' share no common factors). Some perfect ...
s, which are numbers that are the sums of their positive proper
Proper may refer to:
Mathematics
* Proper map, in topology, a property of continuous function between topological spaces, if inverse images of compact subsets are compact
* Proper morphism, in algebraic geometry, an analogue of a proper map for ...
unitary divisor In mathematics, a natural number ''a'' is a unitary divisor (or Hall divisor) of a number ''b'' if ''a'' is a divisor of ''b'' and if ''a'' and \frac are coprime, having no common factor other than 1. Thus, 5 is a unitary divisor of 60, because 5 an ...
s. A sixth unitary number, if discovered, would have at least nine odd prime factors.
Five is conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 19 ...
d to be the only odd untouchable number
An untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer (including the untouchable number itself). That is, these numbers are not in the image of the aliquot sum function. ...
, and if this is the case then five will be the only odd prime number that is not the base of an aliquot tree.
In figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean
* polygon ...
s, 5 is a pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The ...
, with the sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is calle ...
of pentagonal numbers starting: 1, 5, 12, 22, 35, ...
* 5 is a centered tetrahedral number
A centered tetrahedral number is a centered figurate number that represents a tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, ...
: 1, 5, 15, 35, 69, ... Every centered tetrahedral number with an index of 2, 3 or 4 modulo
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the '' modulus'' of the operation).
Given two positive numbers and , modulo (often abbreviated as ) is t ...
5 is divisible by 5.
* 5 is a square pyramidal number
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broa ...
: 1, 5, 14, 30, 55, ... The sum of the first four members is 50 while the fifth indexed member in the sequence is 55.
* 5 is a centered square number
In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each cen ...
: 1, 5, 13, 25, 41, ... The fifth square number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
or 52 is 25, which features in the proportions of the two smallest (3, 4, 5) and (5, 12, 13) ''primitive'' Pythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is ...
s.
The factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
of five, or ! = , is the sum of the first fifteen non-zero positive integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s, and 15th triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
, which in turn is the sum of the first five non-zero positive integers and 5th triangular number. 35, which is the fourth or fifth pentagonal and tetrahedral number
A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron. The th tetrahedral number, , is the sum of the first triangular numbers, that is,
...
, is equal to the sum of the first five triangular numbers: 1, 3, 6, 10, 15.
5 is the value of the central cell
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery ...
of the only non-trivial normal magic square, also called the ''Lo Shu'' square. Its x array of squares has a magic constant
The magic constant or magic sum of a magic square is the sum of numbers in any row, column, or diagonal of the magic square. For example, the magic square shown below has a magic constant of 15. For a normal magic square of order ''n'' – that is ...
of , where the sums of its rows, columns, and diagonals are all equal to fifteen. 5 is also the value of the central cell the only non-trivial order-3 normal magic hexagon that is made of nineteen cells.
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exa ...
equations of degree and below can be solved with radicals, while quintic equation
In algebra, a quintic function is a function of the form
:g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\,
where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a q ...
s of degree 5, and higher, cannot generally be so solved. This is the Abel–Ruffini theorem. This is related to the fact that the symmetric group is a solvable group for ''n'' ⩽ 4 and not solvable for ''n'' ⩾ 5.
Euler's identity, + = , contains five essential number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
s used widely in mathematics: Pi (mathematical constant), Archimedes' constant , e (mathematical constant), Euler's number , the Imaginary number, imaginary number , Unity (mathematics), unity , and zero , which makes this formula a renown example of mathematical beauty, beauty in mathematics.
In geometry
regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
as Star polygon#Regular star polygon, self-intersecting edges that are proportioned in golden ratio, Golden ratio, . Its internal geometry appears prominently in Penrose tilings, and is a Facet (geometry), facet inside Kepler-Poinsot polyhedra, Kepler-Poinsot star polyhedra and Regular 4-polytope#Regular star (Schläfli–Hess) 4-polytopes, Schläfli–Hess star polychora, represented by its Schläfli symbol . A similar figure to the pentagram is a Five-pointed star, five-pointed Simple polygon, simple isotoxal star ☆ without self-intersecting edges. Generally, Star polyhedron, star polytopes that are Regular polytope, regular only exist in dimensions 2 ⩽ < 5.
In graph theory, all Graph theory, graphs with 4 or fewer vertices are Planar graph, planar, however, there is a graph with 5 vertices that is not: ''K''5, the complete graph with 5 vertices, where every pair of distinct vertices in a pentagon is joined by unique edges belonging to a pentagram. By Kuratowski's theorem, a finite graph is planar iff it does not contain a subgraph that is a subdivision of ''K''5, or the complete bipartite utility graph ''K''3,3. A similar graph is the Petersen graph, which is strongly connected and also Planar graph, nonplanar. It is most easily described as graph of a pentagram ''embedded'' inside a pentagon, with a total of 5 Crossing number (graph theory), crossings, a Girth (graph theory), girth of 5, and a Thue number of 5. The Petersen graph, which is also a distance-regular graph, is one of only 5 known Connectivity (graph theory), connected vertex-transitive graphs with no Hamiltonian cycles.Royle, G"Cubic Symmetric Graphs (The Foster Census)."
The automorphism group of the Petersen graph is the symmetric group of group order, order 120 (number), 120 = 5!. The Hadwiger–Nelson problem, chromatic number of the plane is at least five, depending on the choice of Axiom of choice, set-theoretical axioms: the minimum number of Graph coloring, colors required to color the plane such that no pair of points at a distance of 1 has the same color. Whereas the hexagonal Golomb graph and the regular hexagonal tiling generate chromatic numbers of 4 and 7, respectively, a chromatic coloring of 5 can be attained under a more complicated graph where multiple four-coloring Moser spindles are linked so that no monochromatic triples exist in any coloring of the overall graph, as that would generate an equilateral arrangement that tends toward a purely hexagonal Structure (mathematical logic), structure. The Plane (geometry), plane contains a total of five Bravais lattices, or arrays of Point (geometry), points defined by discrete Translation (geometry), translation operations: Hexagonal lattice, hexagonal, Oblique lattice, oblique, Rectangular lattice, rectangular, Rectangular lattice#Bravais lattices, centered rectangular, and Square lattice, square lattices. The plane can also be tiled Pentagonal tiling#Monohedral convex pentagonal tilings, monohedrally with convex pentagonal tiling, pentagons in fifteen different ways, three of which have Laves tilings as special cases. Five points are needed to determine a conic section, in the Five points determine a conic, same way that two points are needed to determine a line. A Veronese surface in the Projective space, projective plane of a conic generalizes a Pairing, linear condition for a point to be contained inside a conic.
 There are Platonic solid, Platonic solids in three-dimensional space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The Regular dodecahedron, dodecahedron in particular contains pentagonal faces, while the Regular icosahedron, icosahedron, its Dual polytope, dual polyhedron, has a vertex figure that is a regular pentagon. There are also :
☆ Uniform polyhedron compound, Regular polyhedron compounds: the stella octangula, compound of five tetrahedra, compound of five cubes, compound of five octahedra, and compound of ten tetrahedra. Icosahedral symmetry is isomorphic to the alternating group on 5 letters of order 120 (number), 120, realized by actions on these uniform polyhedron compounds.
☆ Honeycomb (geometry), Space-filling convex polyhedron, convex polyhedra: the triangular prism, hexagonal prism, cube, truncated octahedron, and gyrobifastigium. While the cube is the only Platonic solid that can tessellate space on its own, the truncated octahedron and the gyrobifastigium are the only Archimedean solid, Archimedean and Johnson solids, respectively, that can also tessellate space with their own copies.
☆ Isohedral figure#Related terms, Cell-transitive Parallelohedron, parallelohedra: any parallelepiped, as well as the rhombic dodecahedron and elongated dodecahedron, and the hexagonal prism and truncated octahedron. The cube is a special case of a parallelepiped, with the rhombic dodecahedron the only Catalan solid to tessellate space on its own.
☆ List of regular polytopes and compounds#Abstract polytopes, Regular abstract polyhedra, which include the excavated dodecahedron and the dodecadodecahedron. They have combinatorial symmetries transitive on List of regular polytopes and compounds#Abstract polytopes, flags of their elements, with Topology, topologies equivalent to that of toroids and the ability to tile the hyperbolic plane.
The 5-cell, or pentatope, is the self-dual fourth-dimensional analogue of the tetrahedron, with Coxeter group symmetry of order 120 (number), 120 = 5Factorial, ! and Mathematical structure, group structure. Made of five tetrahedra, its Petrie polygon is a
There are Platonic solid, Platonic solids in three-dimensional space: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The Regular dodecahedron, dodecahedron in particular contains pentagonal faces, while the Regular icosahedron, icosahedron, its Dual polytope, dual polyhedron, has a vertex figure that is a regular pentagon. There are also :
☆ Uniform polyhedron compound, Regular polyhedron compounds: the stella octangula, compound of five tetrahedra, compound of five cubes, compound of five octahedra, and compound of ten tetrahedra. Icosahedral symmetry is isomorphic to the alternating group on 5 letters of order 120 (number), 120, realized by actions on these uniform polyhedron compounds.
☆ Honeycomb (geometry), Space-filling convex polyhedron, convex polyhedra: the triangular prism, hexagonal prism, cube, truncated octahedron, and gyrobifastigium. While the cube is the only Platonic solid that can tessellate space on its own, the truncated octahedron and the gyrobifastigium are the only Archimedean solid, Archimedean and Johnson solids, respectively, that can also tessellate space with their own copies.
☆ Isohedral figure#Related terms, Cell-transitive Parallelohedron, parallelohedra: any parallelepiped, as well as the rhombic dodecahedron and elongated dodecahedron, and the hexagonal prism and truncated octahedron. The cube is a special case of a parallelepiped, with the rhombic dodecahedron the only Catalan solid to tessellate space on its own.
☆ List of regular polytopes and compounds#Abstract polytopes, Regular abstract polyhedra, which include the excavated dodecahedron and the dodecadodecahedron. They have combinatorial symmetries transitive on List of regular polytopes and compounds#Abstract polytopes, flags of their elements, with Topology, topologies equivalent to that of toroids and the ability to tile the hyperbolic plane.
The 5-cell, or pentatope, is the self-dual fourth-dimensional analogue of the tetrahedron, with Coxeter group symmetry of order 120 (number), 120 = 5Factorial, ! and Mathematical structure, group structure. Made of five tetrahedra, its Petrie polygon is a regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
and its orthographic projection is equivalent to the complete graph ''K''5. It is one of six Uniform 4-polytope, regular 4-polytopes, made of thirty-one Simplex#Elements, elements: five Vertex (geometry), vertices, ten Edge (geometry), edges, ten Face (geometry), faces, five Regular tetrahedron, tetrahedral cells and one Face (geometry)#Facet or (n − 1)-face, 4-face.
*A 120-cell, regular 120-cell, the dual ''polychoron'' to the regular 600-cell, can fit one hundred and twenty 5-cells. Also, five 24-cells fit inside a small stellated 120-cell, the first stellation of the 120-cell.
*A subset of the vertices of the small stellated 120-cell are matched by the great duoantiprism, great duoantiprism star, which is the only Uniform polytope, uniform nonconvex duoantiprism, ''duoantiprismatic'' solution in the fourth dimension, constructed from the polytope cartesian product and made of fifty tetrahedra, ten pentagrammic crossed antiprisms, ten pentagonal antiprisms, and fifty vertices.
*The grand antiprism, which is the only known Wythoff construction, non-Wythoffian construction of a uniform polychoron, is made of twenty pentagonal antiprisms and three hundred tetrahedra, with a total of one hundred vertices and five hundred edges.
*The Abstract polytope, abstract four-dimensional 57-cell is made of fifty-seven Hemi-icosahedron, hemi-icosahedral cells, in-which five surround each edge. The 11-cell, another abstract 4-polytope with eleven vertices and fifty-five edges, is made of eleven Hemi-dodecahedron, hemi-dodecahedral cells each with fifteen dodecahedra. The n-skeleton, skeleton of the hemi-dodecahedron is the Petersen graph.
Overall, the fourth dimension contains five Uniform 4-polytope#Convex uniform 4-polytopes, Weyl groups that form a finite number of Uniform 4-polytope#Enumeration, uniform polychora: A4 polytope, , B4 polytope, , D4 polytope, , F4 polytope, , and H4 polytope, , with four of these Coxeter groups capable of generating the same finite forms without ; accompanied by a fifth or sixth general group of unique Uniform 4-polytope#Prismatic uniform 4-polytopes, 4-prisms of Platonic and Archimedean solids. There are also a total of five Coxeter groups that generate non-prismatic Uniform 5-polytope#Regular and uniform honeycombs, Eucledian honeycombs in 4-space, alongside five Uniform 5-polytope#Regular and uniform hyperbolic honeycombs, compact hyperbolic Coxeter groups that generate five regular Uniform 5-polytope#Compact regular tessellations of hyperbolic 4-space, compact hyperbolic honeycombs with finite Facet (geometry), facets, as with the order-5 5-cell honeycomb and the order-5 120-cell honeycomb, both of which have five cells around each face. Compact hyperbolic honeycombs only exist through the fourth dimension, or Coxeter-Dynkin diagram#Ranks 4–5, rank 5, with Coxeter–Dynkin diagram#Paracompact (Koszul simplex groups), paracompact hyperbolic solutions existing through rank 10. Likewise, analogues of three-dimensional icosahedral symmetry or four-dimensional H4 polytope, symmetry do not exist in dimensions ''n'' ⩾ 5; however, there is the uniform polytope, uniform Uniform 5-polytope#H4 × A1, prismatic group × in the fifth dimension which contains Prism (geometry), prisms of regular and uniform Uniform 4-polytope, 4-polytopes that have symmetry.
The 5-simplex is the Five-dimensional space, five-dimensional analogue of the 5-cell, or 4-simplex; the fifth iteration of -simplexes in any dimensions. The 5-simplex has the Coxeter group as its symmetry group, of order 720 = 6Factorial, !, whose group structure is represented by the symmetric group , the only finite symmetric group which has an outer automorphism. The 5-cube, made of ten tesseracts and the 5-cell as its vertex figure, is also regular and one of thirty-one uniform 5-polytopes under the Coxeter Uniform 5-polytope#The B5 family, hypercubic group. The demipenteract, with one hundred and twenty Cell (geometry), cells, is the only fifth-dimensional semiregular polytope, and has the rectified 5-cell as its vertex figure, which is one of only three semiregular 4-polytopes alongside the rectified 600-cell and the snub 24-cell. In the fifth dimension, there are five regular paracompact honeycombs, all with Infinity, infinite Facet (geometry), facets and vertex figures. There are exclusively twelve Complex polytope#Regular complex 5-apeirotopes and higher, complex aperiotopes in Complex coordinate space, complex spaces of dimensions ⩾ , with fifteen in and sixteen in ; alongside Complex polytope#Enumeration of regular complex 5-polytopes, complex polytopes in and higher under simplex, hypercube, hypercubic and orthoplex groups, the latter with Complex polytope#van Oss polygon, van Oss polytopes.
There are five Simple Lie group#Exceptional cases, exceptional Lie groups: G2 (mathematics), , F4 (mathematics), , E6 (mathematics), , E7 (mathematics), , and E8 (mathematics), . The Faithful representation, smallest of these, , can be represented in five-dimensional complex space and Projective geometry, projected in the same number of dimensions as a Ball (geometry), ball rolling on top of another ball, whose motion is described in two-dimensional space. , the largest of all five exceptional groups, also contains the other four as subgroups and is constructed with one hundred and twenty quaternionic Icosian, unit icosians that make up the vertices of the 600-cell. There are also five solvable groups that are excluded from finite simple groups of Group of Lie type, Lie type.
The five Mathieu groups constitute the Sporadic group#First generation (5 groups): the Mathieu groups, first generation in the Sporadic groups#Happy Family, happy family of sporadic groups. These are also the first five sporadic groups Classification of finite simple groups#Timeline of the proof, to have been described, defined as Mathieu groups#Multiply transitive groups, multiply transitive permutation groups on Group object, objects, with Element (mathematics), ∈ . In particular, , the smallest of all sporadic groups, has a rank 3 action on fifty-five points from an Induced representation, induced action on unordered pairs, as well as two five-dimensional space, five-dimensional Faithful representation, faithful complex irreducible representations over the Field (mathematics), field with three elements, which is the lowest irreducible dimensional representation of all sporadic group over their respective fields with ''n'' elements. Of precisely five different conjugacy classes of maximal subgroups of , one is the Almost simple group, almost simple symmetric group Symmetric group#Low degree groups, (of order 5Factorial, !), and another is , also almost simple, that functions as a point stabilizer which has as its largest prime factor in its group order: 24·32·5 = 2·3·4·5·6 = 8·9·10 = 720. On the other hand, whereas is sharply 4-transitive, is Mathieu groups#Multiply transitive groups, sharply 5-transitive and is 5-transitive, and as such they are the only two 5-transitive groups that are not symmetric groups or alternating groups. has the first five prime numbers as its distinct prime factors in its order of 27· 32·5· 7· 11, and is the smallest of five sporadic groups with five distinct prime factors in their order. All Mathieu groups are subgroups of , which under the Witt design of Steiner system#The Steiner system S(5, 8, 24), Steiner system S(5, 8, 24) emerges a construction of the Binary Golay code, extended binary Golay code that has as its automorphism group. generates ''octads'' from code words of Hamming weight 8 from the extended binary Golay code, one of five different Hamming weights the extended binary Golay code uses: 0, 8, 12 (number), 12, 16 (number), 16, and 24 (number), 24. The Witt design and the extended binary Golay code in turn can be used to generate a faithful construction of the 24-dimensional Leech lattice Λ24, which is the subject of the Sporadic group#Second generation (7 groups): the Leech lattice, second generation of seven sporadic groups that are subquotients of the automorphism of the Leech lattice, Conway group, Conway group .
There are five Supersingular prime (moonshine theory), non-supersingular primes: 37 (number), 37, 43 (number), 43, 53 (number), 53, 61 (number), 61, and 67 (number), 67, all smaller than the largest of fifteen supersingular prime divisors of the Monster group, friendly giant, 71 (number), 71.
List of basic calculations
In decimal
5 is the only prime number to end in the digit 5 in decimal because all other numbers written with a 5 in the Positional notation, ones place are multiples of five, which makes it a 1-automorphic number. All multiples of 5 will end in either 5 or , and Fraction (mathematics)#Vulgar, proper, and improper fractions, vulgar fractions with 5 or in the fraction (mathematics), denominator do not yield infinite decimal expansions because they are prime factors of 10, the base. In the Power (mathematics), powers of 5, every power ends with the number five, and from 53 onward, if the exponent isodd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
, then the hundreds digit is 1, and if it is even, the hundreds digit is 6.
A number raised to the fifth power always ends in the same digit as .
Evolution of the Arabic digit

Science
*The atomic number of boron. *The number of appendages on most sea star, starfish, which exhibit symmetry (biology)#Pentamerism, pentamerism. *The most destructive known tropical cyclone, hurricanes rate as Saffir–Simpson hurricane wind scale#Category 5, Category 5 on the Saffir–Simpson hurricane wind scale. *The most destructive known tornadoes rate an F-5 on the Fujita scale or EF-5 on the Enhanced Fujita scale.Astronomy
*Messier object Messier 5, M5, a magnitude 7.0 globular cluster in the constellation Serpens. *The New General Catalogue]object
NGC 5, a apparent magnitude, magnitude 13 spiral galaxy in the constellation Andromeda (constellation), Andromeda. *The Roman numeral V stands for dwarfs (main sequence stars) in the stellar classification, Yerkes spectral classification scheme. *The Roman numeral V (usually) stands for the fifth-discovered satellite of a planet or minor planet (e.g. Amalthea (moon), Jupiter V). *There are five Lagrangian points in a two-body system.
Biology
*There are generally considered to be five senses. *The five basic tastes are sweetness, sweet, taste#Saltiness, salty, taste#Sourness, sour, taste#Bitterness, bitter, and umami. *Almost all amphibians, reptiles, and mammals which have fingers or toes have five of them on each extremity.Computing
*5 is the ASCII code of the Enquiry character, which is abbreviated to ENQ.Religion and culture
Hinduism
*The god Shiva has five faces and his mantra is also called (five-worded) mantra. *The goddess Saraswati, goddess of knowledge and intellectual is associated with or the number 5. *There are Pancha Bhoota, five elements in the universe according to Hindu cosmology: (earth, fire, water, air and space respectively). *The most sacred tree in Hinduism has 5 leaves in every leaf stunt. *Most of the flowers have 5 petals in them. *The epic Mahabharata revolves around the battle between Duryodhana and his 99 other brothers and the 5 pandava princes—Yudhisthira, Dharma, Arjuna, Bhima, Nakula and Sahadeva.Christianity
*There are traditionally Five Wounds, five wounds of Jesus Christ in Christianity: the Flagellation of Christ, Scourging at the Pillar, Crown of Thorns, the Crowning with Thorns, the wounds in Christ's hands, the wounds in Christ's feet, and the Holy Lance, Side Wound of Christ.Gnosticism
*The number five was an important symbolic number in Manichaeism, with heavenly beings, concepts, and others often grouped in sets of five. *Five Seals in Sethianism *Five Trees in the Gospel of ThomasIslam
*The Five Pillars of Islam *Muslims pray to Allah five times a day *According to Shia Muslims, the Panjetan-e-Pak, Panjetan or the Five Holy Purified Ones are the members of Muhammad's family: Muhammad, Ali, Fatimah, Hasan ibn Ali, Hasan, and Husayn ibn Ali, Husayn and are often symbolically represented by an image of the Hamsa, Khamsa.Judaism
*The Torah contains five books—Book of Genesis, Genesis, Book of Exodus, Exodus, Book of Leviticus, Leviticus, Book of Numbers, Numbers, and Book of Deuteronomy, Deuteronomy—which are collectively called the Five Books of Moses, the Pentateuch (Greek language, Greek for "five containers", referring to the scroll cases in which the books were kept), or Chumash (Judaism), Humash (, Hebrew language, Hebrew for "fifth"). *The book of Psalms is arranged into five books, paralleling the Five Books of Moses. *The Hamsa, Khamsa, an ancient symbol shaped like a hand with four fingers and one thumb, is used as a protective amulet by Jews; that same symbol is also very popular in Arabic culture, known to protect from envy and the evil eye.Sikhism
*The five sacred Sikh symbols prescribed by Guru Gobind Singh are commonly known as or the "The Five Ks, Five Ks" because they start with letter K representing in the Punjabi language's Gurmukhi script. They are: (unshorn hair), (the comb), (the steel bracelet), (the soldier's shorts), and (the sword) (in Gurmukhi: ). Also, there are five deadly evils: (lust), (anger), (attachment), (greed), and (ego).Daoism
*Wuxing (Chinese philosophy), 5 Elements *Three Sovereigns and Five Emperors, 5 EmperorsOther religions and cultures
*According to ancient Greek philosophers such as Aristotle, the universe is made up of five classical elements: water (classical element), water, earth (classical element), earth, air (classical element), air, fire (classical element), fire, and aether (classical element), ether. This concept was later adopted by medieval alchemists and more recently by practitioners of Neo-Pagan religions such as Wicca. *The pentagram, or five-pointed star, bears religious significance in various faiths including Baháʼí Faith, Baháʼí, Christianity, Freemasonry, Satanism, Taoism, Thelema, and Wicca. *In Cantonese, "five" sounds like the word "not" (character: ). When five appears in front of a lucky number, e.g. "58", the result is considered unlucky. *In East Asian tradition, there are five elements: (water (Wu Xing), water, fire (Wu Xing), fire, earth (Wu Xing), earth, tree (Wu Xing), wood, and metal (Wu Xing), metal). The Japanese language, Japanese names for the week-day names, days of the week, Tuesday through Saturday, come from these elements via the identification of the elements with the Classical planet, five planets visible with the naked eye. Also, the traditional Japanese calendar has a five-day weekly cycle that can be still observed in printed mixed calendars combining Western, Chinese-Buddhist, and Japanese names for each weekday. *In numerology, 5 or a series of 555 (number), 555, is often associated with change, evolution, love and abundance. *Members of The Nation of Gods and Earths, a primarily African American religious organization, call themselves the "Five-Percenters" because they believe that only 5% of mankind is truly enlightened.Art, entertainment, and media
Fictional entities
*James the Red Engine, a fictional character numbered 5. *Johnny 5 is the lead character in the film ''Short Circuit'' (1986) *Number Five is a character in Lorien Legacies *Sankara Stones, five magical rocks in ''Indiana Jones and the Temple of Doom'' that are sought by the Thuggees for evil purposes *The Mach Five , the racing car Speed Racer ( in the Japanese version) drives in the anime series of the same name (known as "Mach Go! Go! Go!" in Japan) *In the works of J. R. R. Tolkien, five wizards (Saruman, Gandalf, Radagast, Blue Wizards, Alatar and Pallando) are sent to Middle-earth to aid against the threat of the Dark Lord Sauron *In the ''A Song of Ice and Fire'' series, the War of the Five Kings is fought between different claimants to the Iron Throne of Westeros, as well as to the thrones of the individual regions of Westeros (Joffrey Baratheon, Stannis Baratheon, Renly Baratheon, Robb Stark and Balon Greyjoy) *In ''The Wheel of Time'' series, the "Emond's Field Five" are a group of five of the series' main characters who all come from the village of Emond's Field (Rand al'Thor, Matrim Cauthon, Perrin Aybara, Egwene al'Vere and Nynaeve al'Meara) *Myst (series), ''Myst'' uses the number 5 as a unique base counting system. In ''The Myst Reader'' series, it is further explained that the number 5 is considered a holy number in the fictional D'ni society. *Number Five is also a character in The Umbrella Academy comic book and TV series adaptationFilms
*Towards the end of the film ''Monty Python and the Holy Grail'' (1975), the character of King Arthur repeatedly confuses the number five with the number 3, three. *''Five Go Mad in Dorset'' (1982) was the first of the long-running series of ''The Comic Strip, The Comic Strip Presents...'' television comedy films *''The Fifth Element'' (1997), a science fiction film * ''Fast Five'' (2011), the fifth installment of the The Fast and the Furious (series), ''Fast and Furious'' film series. *''V for Vendetta (film), V for Vendetta'' (2005), produced by Warner Bros., directed by James McTeigue, and adapted from Alan Moore's graphic novel ''V for Vendetta'' prominently features number 5 and Roman Numeral V; the story is based on the historical event in which a group of men attempted to destroy Parliament on November 5, 1605Music
Groups
*Five (group), a UK Boy band *The Five (composers), 19th-century Russian composers *5 Seconds of Summer, pop band that originated in Sydney, Australia *Five Americans, American rock band active 1965–1969 *Five Finger Death Punch, American heavy metal band from Las Vegas, Nevada. Active 2005–present *Five Man Electrical Band, Canadian rock group billed (and active) as the Five Man Electrical Band, 1969–1975 *Maroon 5, American pop rock band that originated in Los Angeles, California *MC5, American punk rock band *Pentatonix, a Grammy-winning a cappella group originated in Arlington, Texas *The 5th Dimension, American pop vocal group, active 1977–present *The Dave Clark Five, a.k.a. DC5, an English pop rock group comprising Dave Clark (musician), Dave Clark, Lenny Davidson, Rick Huxley, Denis Payton, and Mike Smith (Dave Clark Five), Mike Smith; active 1958–1970 *The Jackson 5, American pop rock group featuring various members of the Jackson family; they were billed (and active) as The Jackson 5, 1966–1975 *Hi-5 (Australian group), Hi-5, Australian pop kids group, where it has several international adaptations, and several members throughout the history of the band. It was also a TV show. *We Five: American folk rock group active 1965–1967 and 1968–1977 *Grandmaster Flash and the Furious Five: American rap group, 1970–80's *Fifth Harmony, an American girl group. *Ben Folds Five, an American alternative rock trio, 1993–2000, 2008 and 2011–2013 *R5 (band), an American pop and alternative rock group, 2009–2018Other uses
*A perfect fifth is the most consonant harmony, and is the basis for most western tuning systems. *Modern musical notation uses a staff (music), musical staff made of five horizontal lines. *In harmonics – the fifth harmonic series (music), partial (or 4th overtone) of a fundamental frequency, fundamental has a frequency ratio of 5:1 to the frequency of that fundamental. This ratio corresponds to the interval of 2 octaves plus a pure major third. Thus, the interval of 5:4 is the interval of the pure third. A major and minor, major Triad (music), triad chord (music), chord when played in just intonation (most often the case in a cappella vocal ensemble singing), will contain such a pure major third. *The number of completed, numbered piano concertos of Ludwig van Beethoven, Sergei Prokofiev, and Camille Saint-Saëns. *Using the Latin root, five musicians are called a quintet. *A scale with five notes per octave is called a pentatonic scale. *Five is the lowest possible number that can be the top number of a time signature with an asymmetric meter (music), meter.Television
;Stations *Channel 5 (UK), a television channel that broadcasts in the United Kingdom *5 (TV channel) (''formerly known as ABC 5 and TV5'') (DWET-TV channel 5 In Metro Manila) a television network in the Philippines. ; ;Series *''Babylon 5'', a science fiction television series *The number 5 features in the television series Battlestar Galactica (2004 TV series), ''Battlestar Galactica'' in regards to the Final Five (Battlestar Galactica), Final Five cylons and the Temple of Five *Hi-5 (Australian TV series), ''Hi-5'' (Australian TV series), a television series from Australia *Hi-5 (UK TV series), ''Hi-5'' (UK TV series), a television show from the United Kingdom *Hi-5 Philippines, ''Hi-5'' Philippines a television show from the Philippines *''Odyssey 5'', a 2002 science fiction television series *''Tillbaka till Vintergatan'', a Swedish children's television series featuring a character named "Femman" (meaning five), who can only utter the word 'five'. *''The Five (talk show), The Five'' The Five (talk show), (talk show): Fox News Channel roundtable current events television show, premiered 2011, so-named for its panel of five commentators. *''Yes! PreCure 5'' is a 2007 anime series which follows the adventures of Nozomi and her friends. It is also followed by the 2008 sequel ''Yes! Pretty Cure 5 GoGo!'' *''The Quintessential Quintuplets'' is a 2019 slice of life romance anime series which follows the everyday life of five identical quintuplets and their interactions with their tutor. It has two seasons, and a final movie is scheduled in summer 2022. *Hawaii Five-0 (2010 TV series), ''Hawaii Five-0'', CBS American TV series.Literature
*The Famous Five (novel series), ''The Famous Five'' is a series of children's books by British writer Enid Blyton *''The Power of Five'' is a series of children's books by British writer and screenwriter Anthony Horowitz *''The Fall of Five'' is a book written under the collective pseudonym Pittacus Lore in the series ''Lorien Legacies'' *''The Book of Five Rings'' is a text on kenjutsu and the martial arts in general, written by the swordsman Miyamoto Musashi circa 1645 *''Slaughterhouse-Five'' is a book by Kurt Vonnegut about World War IISports
*The Olympic Games have five interlocked rings as their symbol, representing the number of inhabited continents represented by the Olympians (Europe, Asia, Africa, Australia and Oceania, and the Americas). * In AFL Women's, the top level of Women's Australian rules football, women's Australian rules football, each team is allowed 5 "Interchange (Australian rules football), interchanges" (substitute players), who can be freely substituted at any time. *In Baseball scorekeeping#Defensive positions, baseball scorekeeping, the number 5 represents the third baseman's position. *In basketball: **The number 5 is used to represent the position of center (basketball), center. **Each team has five players on the court at a given time. Thus, the phrase "five on five" is commonly used to describe standard competitive basketball. **The Five-second rule (basketball), "5-second rule" refers to several related rules designed to promote continuous play. In all cases, violation of the rule results in a turnover. **Under the FIBA (used for all international play, and most non-US leagues) and College basketball, NCAA women's rule sets, a team begins shooting Bonus (basketball), bonus free throws once its opponent has committed five Personal foul (basketball), personal fouls in a quarter. **Under the FIBA rules, A player fouls out and must leave the game after committing five fouls *Five-a-side football is a variation of association football in which each team fields five players. *In ice hockey: ** A major penalty lasts five minutes. ** There are five different ways that a player can score a goal (teams at even strength, team on the power play, team playing shorthanded, penalty shot, and empty net). ** The area between the goaltender's legs is known as the five-hole. *In most rugby league competitions, the starting Rugby league positions#Wing, left wing wears this number. An exception is the Super League, which uses static squad numbering. *In rugby union: ** A Try (rugby), try is worth 5 points. ** One of the two starting Lock (rugby union), lock forwards wears number 5, and usually jumps at number 4 in the line-out (rugby union), line-out. ** In the National Rugby League (France), French variation of the Rugby union bonus points system, bonus points system, a bonus point in the league standings is awarded to a team that loses by 5 or fewer points.Technology
*5 is the most common number of gears for automobiles with manual transmission. *In radio communication, the term "Five by five" is used to indicate perfect signal strength and clarity. *On almost all devices with a numeric keypad such as telephones, computers, etc., the 5 key has a raised dot or raised bar to make dialing easier. Persons who are blind or have low vision find it useful to be able to feel the keys of a telephone. All other numbers can be found with their relative position around the 5 button (on computer keyboards, the 5 key of the numeric keypad, numpad has the raised dot or bar, but the 5 key that shifts with % does not). *On most telephones, the 5 key is associated with the letters J, K, and L, but on some of the BlackBerry phones, it is the key for G and H. *The Pentium, coined by Intel Corporation, is a fifth-generation x86 architecture microprocessor. *The resin identification code used in recycling to identify polypropylene.Miscellaneous fields
Five can refer to: *"Give me five" is a common phrase used preceding a high five. *An informal term for the British Security Service, MI5. *Five babies born at one time are multiple birth, quintuplets. The most famous set of quintuplets were the Dionne quintuplets born in the 1930s. *In the United States legal system, the Fifth Amendment to the United States Constitution can be referred to in court as "pleading the fifth", absolving the defendant from self-incrimination. *Pentameter is verse with five repeating feet per line; iambic pentameter was the most popular form in William Shakespeare, Shakespeare. *Aether (classical element), Quintessence, meaning "fifth element", refers to the elusive fifth element that completes the basic four elements (water, fire, air, and earth) *The designation of an Interstate Highway System, Interstate Highway (Interstate 5) that runs from San Diego, California to Blaine, Washington. In addition, all major north-south Interstate Highways in the United States end in 5. *In the computer game ''Riven'', 5 is considered a holy number, and is a recurring theme throughout the game, appearing in hundreds of places, from the number of islands in the game to the number of bolts on pieces of machinery. *''The Garden of Cyrus'' (1658) by Sir Thomas Browne is a Pythagorean discourse based upon the number 5. *The holy number of Discordianism, as dictated by the Discordianism#Law of Fives, Law of Fives. *The number of Justices on the Supreme Court of the United States necessary to render a majority decision. *The number of dots in a quincunx. *The number of permanent members with veto power on the United Nations Security Council. *The number of sides and the number of angles in a pentagon. *The number of points in a pentagram. *The number of Korotkoff sounds when measuring blood pressure *The drink Five Alive is named for its five ingredients. The drink Punch (drink), punch derives its name after the Sanskrit पञ्च (pañc) for having five ingredients. *The Keating Five were five United States Senate, United States Senators accused of corruption in 1989. *The Inferior Five: Merryman, Awkwardman, The Blimp, White Feather, and Dumb Bunny. DC Comics parody superhero team. *Chanel No. 5, No. 5 is the name of the iconic fragrance created by Coco Chanel. *The Committee of Five was delegated to draft the United States United States Declaration of Independence, Declaration of Independence. *The five-second rule is a commonly used rule of thumb for dropped food. *555 95472, usually referred to simply as 5, is a minor male character in the comic strip ''Peanuts''.See also
*Five Families *Five Nations (disambiguation) *555 (number) *List of highways numbered 5References
*Wells, D. ''The Penguin Dictionary of Curious and Interesting Numbers'' London: Penguin Group. (1987): 58–67External links
* *The Number 5
{{DEFAULTSORT:5 (Number) Integers 5 (number)