ω-limit Cycle

In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912).

Definition

We consider a two-dimensional dynamical system of the form
$x'(t)=V(x(t))$
where
$V : \R^2 \to \R^2$
is a smooth function. A ''trajectory'' of this system is some smooth function $x(t)$ with values in $\mathbb^2$ which satisfies this differential equation. Such a trajectory is called ''closed'' (or ''periodic'') if it is not constant but returns to its starting point, i.e. if there exists some $t_0>0$ such that $x(t + t_0) = x(t)$ for all $t \in \R$. An orbit is the image of a trajectory, a subset of $\R^2$. A ''closed orbit'', or ''cycle'', is the image of a closed trajectory. A ''limit cycle'' is a cycle which is the limit set of some other trajectory.

Properties

By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve.

Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching $+ \infty$, then there is a neighborhood around the limit cycle such that ''all'' trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching $+ \infty$. The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching $- \infty$, and also for trajectories in the exterior approaching the limit cycle.

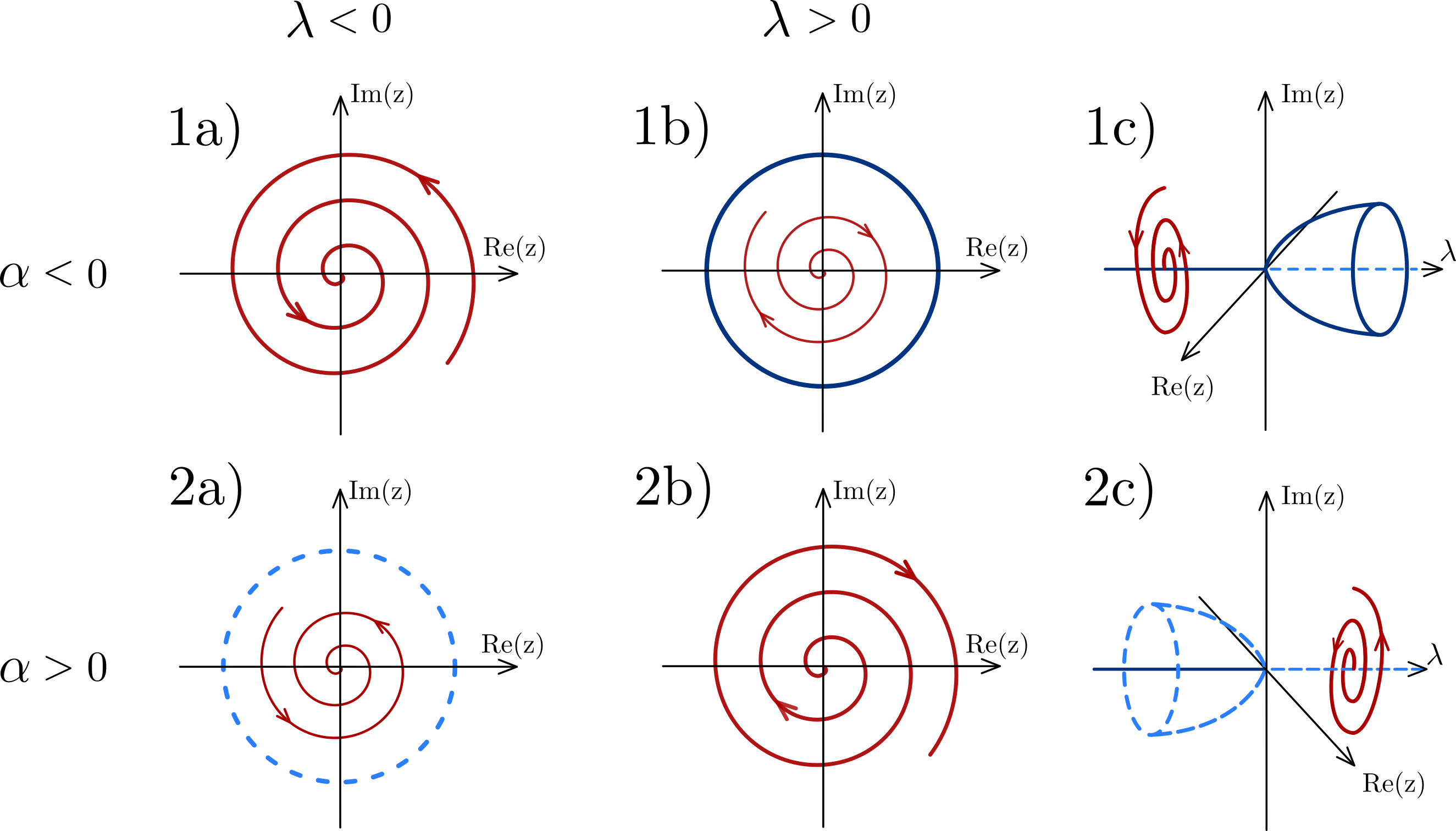
Stable, unstable and semi-stable limit cycles

In the case where all the neighboring trajectories approach the limit cycle as time approaches infinity, it is called a ''stable'' or ''attractive'' limit cycle (ω-limit cycle). If instead, all neighboring trajectories approach it as time approaches negative infinity, then it is an ''unstable'' limit cycle (α-limit cycle). If there is a neighboring trajectory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a ''semi-stable'' limit cycle. There are also limit cycles that are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which would not be limit cycles).

Stable limit cycles are examples of attractors. They imply self-sustained oscillations: the closed trajectory describes the perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.

Finding limit cycles

Every closed trajectory contains within its interior a stationary point of the system, i.e. a point $p$ where $V'(p) = 0$. The Bendixson–Dulac theorem and the Poincaré–Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.

Open problems

Finding limit cycles, in general, is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of Hilbert's sixteenth problem. It is unknown, for instance, whether there is any system $x' = V(x)$ in the plane where both components of $V$ are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles.

Applications

Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:

* Aerodynamic limit-cycle oscillations
* The Hodgkin–Huxley model for action potentials in neurons.
* The Sel'kov model of glycolysis.
* The daily oscillations in gene expression, hormone levels and body temperature of animals, which are part of the circadian rhythm, although this is contradicted by more recent evidence.
* The migration of cancer cells in confining micro-environments follows limit cycle oscillations.
* Some non-linear electrical circuits exhibit limit cycle oscillations, which inspired the original Van der Pol model.
*The control of respiration and hematopoiesis, as appearing in the Mackey-Glass equations.

See also

* Attractor
* Hyperbolic set
* Periodic point
* Self-oscillation
* Stable manifold

References

Further reading

*
*
* Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002.
* Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002.
* Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005.
* Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006.
* Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/#

External links

* {{cite web , url=https://planetmath.org/limitcycle , website=planetmath.org , title=limit cycle , access-date=2019-07-06

Limit sets
Nonlinear systems
Dynamical systems