Ãœber Quantentheoretischer Umdeutung on:
[Wikipedia]
[Google]
[Amazon]
In the
 In
In
 By means of an intense series of mathematical analogies that some physicists have termed "magical", Heisenberg wrote out an equation that is the quantum mechanical analog for the classical computation of intensities:
This general format indicates that some term is to be computed by summing up all of the products of some group of terms by some related group of terms . There will potentially be an infinite series of terms and their matching terms. Each of these multiplications has as its factors two measurements that pertain to sequential downward transitions between energy states of an electron. This type of rule differentiates matrix mechanics from the kind of physics familiar in everyday life because the important values are where (in what energy state or "orbital") the electron begins and in what energy state it ends, not what the electron is doing while in one or another state.
If and both refer to lists of frequencies, for instance, the calculation proceeds as follows:
Multiply the frequency for a change of energy from state to state by the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'', and to that add the product found by multiplying the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'' by the frequency for a change of energy from state ''n'' − ''b'' to state ''n'' − ''c'', and so forth. Symbolically, that is:
:
(According to the convention used, represents a higher energy state than , so a transition from to would indicate that an electron has accepted energy from an incoming photon and has risen to a higher orbital, while a transition from to would represent an electron falling to a lower orbital and emitting a photon.)
It would be easy to perform each individual step of this process for some measured quantity. For instance, the boxed formula at the head of this article gives each needed wavelength in sequence. The values calculated could very easily be filled into a grid as described below. However, since the series is infinite, nobody could do the entire set of calculations.
Heisenberg originally devised this equation to enable himself to multiply two measurements of the same kind (amplitudes), so it happened not to matter in which order they were multiplied. Heisenberg noticed, however that if he tried to use the same schema to multiply two variables, such as momentum, ''p'', and displacement, ''q'', then "a significant difficulty arises". It turns out that multiplying a matrix of ''p'' by a matrix of ''q'' gives a different result from multiplying a matrix of ''q'' by a matrix of ''p''. It only made a tiny bit of difference, but that difference could never be reduced below a certain limit, and that limit involved the
By means of an intense series of mathematical analogies that some physicists have termed "magical", Heisenberg wrote out an equation that is the quantum mechanical analog for the classical computation of intensities:
This general format indicates that some term is to be computed by summing up all of the products of some group of terms by some related group of terms . There will potentially be an infinite series of terms and their matching terms. Each of these multiplications has as its factors two measurements that pertain to sequential downward transitions between energy states of an electron. This type of rule differentiates matrix mechanics from the kind of physics familiar in everyday life because the important values are where (in what energy state or "orbital") the electron begins and in what energy state it ends, not what the electron is doing while in one or another state.
If and both refer to lists of frequencies, for instance, the calculation proceeds as follows:
Multiply the frequency for a change of energy from state to state by the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'', and to that add the product found by multiplying the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'' by the frequency for a change of energy from state ''n'' − ''b'' to state ''n'' − ''c'', and so forth. Symbolically, that is:
:
(According to the convention used, represents a higher energy state than , so a transition from to would indicate that an electron has accepted energy from an incoming photon and has risen to a higher orbital, while a transition from to would represent an electron falling to a lower orbital and emitting a photon.)
It would be easy to perform each individual step of this process for some measured quantity. For instance, the boxed formula at the head of this article gives each needed wavelength in sequence. The values calculated could very easily be filled into a grid as described below. However, since the series is infinite, nobody could do the entire set of calculations.
Heisenberg originally devised this equation to enable himself to multiply two measurements of the same kind (amplitudes), so it happened not to matter in which order they were multiplied. Heisenberg noticed, however that if he tried to use the same schema to multiply two variables, such as momentum, ''p'', and displacement, ''q'', then "a significant difficulty arises". It turns out that multiplying a matrix of ''p'' by a matrix of ''q'' gives a different result from multiplying a matrix of ''q'' by a matrix of ''p''. It only made a tiny bit of difference, but that difference could never be reduced below a certain limit, and that limit involved the
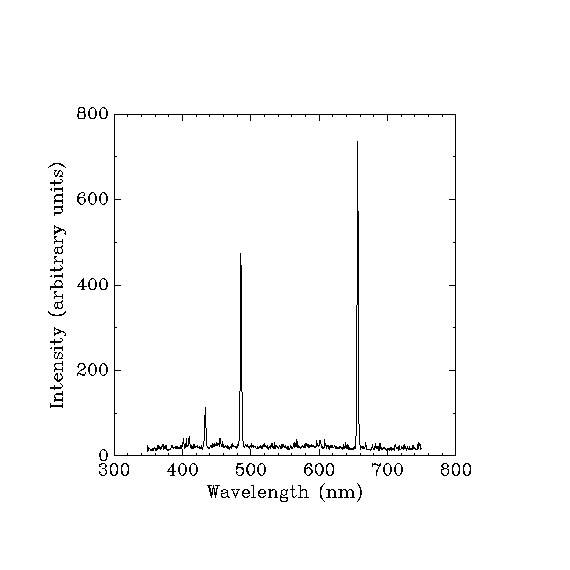
 Werner Heisenberg used the idea that since classical physics is correct when it applies to phenomena in the world of things larger than atoms and molecules, it must stand as a special case of a more inclusive quantum theoretical model. So he hoped that he could modify quantum physics in such a way that when the parameters were on the scale of everyday objects it would look just like classical physics, but when the parameters were pulled down to the atomic scale the discontinuities seen in things like the widely spaced frequencies of the visible hydrogen bright line spectrum would come back into sight.
The one thing that people at that time most wanted to understand about hydrogen radiation was how to predict or account for the intensities of the lines in its spectrum. Although Heisenberg did not know it at the time, the general format he worked out to express his new way of working with quantum theoretical calculations can serve as a recipe for two matrices and how to multiply them.
The ''Umdeutung'' paper does not mention matrices. Heisenberg's great advance was the "scheme which was capable in principle of determining uniquely the relevant physical qualities (transition frequencies and amplitudes)" of hydrogen radiation.
After Heisenberg wrote the ''Umdeutung'' paper, he turned it over to one of his senior colleagues for any needed corrections and went on vacation.
Werner Heisenberg used the idea that since classical physics is correct when it applies to phenomena in the world of things larger than atoms and molecules, it must stand as a special case of a more inclusive quantum theoretical model. So he hoped that he could modify quantum physics in such a way that when the parameters were on the scale of everyday objects it would look just like classical physics, but when the parameters were pulled down to the atomic scale the discontinuities seen in things like the widely spaced frequencies of the visible hydrogen bright line spectrum would come back into sight.
The one thing that people at that time most wanted to understand about hydrogen radiation was how to predict or account for the intensities of the lines in its spectrum. Although Heisenberg did not know it at the time, the general format he worked out to express his new way of working with quantum theoretical calculations can serve as a recipe for two matrices and how to multiply them.
The ''Umdeutung'' paper does not mention matrices. Heisenberg's great advance was the "scheme which was capable in principle of determining uniquely the relevant physical qualities (transition frequencies and amplitudes)" of hydrogen radiation.
After Heisenberg wrote the ''Umdeutung'' paper, he turned it over to one of his senior colleagues for any needed corrections and went on vacation.
"Quantum-theoretical reinterpretation of kinematic and mechanical relations"
by B. L. van der Waerden may be found in * The crucial reinterpretation synthesis of Heisenberg's paper, which introduces the contemporary language employed now. {{DEFAULTSORT:Ueber quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen Historical physics publications 1925 in science 1925 documents 1925 in Germany Physics papers Works originally published in German magazines Works originally published in science and technology magazines Werner Heisenberg
history of physics
Physics is a branch of science in which the primary objects of study are matter and energy. These topics were discussed across many cultures in ancient times by philosophers, but they had no means to distinguish causes of natural phenomena fro ...
, "On the quantum-theoretical reinterpretation of kinematical and mechanical relationships"
(), also known as the ''Umdeutung'' (reinterpretation) paper, was a breakthrough article in quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
written by Werner Heisenberg
Werner Karl Heisenberg (; ; 5 December 1901 – 1 February 1976) was a German theoretical physicist, one of the main pioneers of the theory of quantum mechanics and a principal scientist in the German nuclear program during World War II.
He pub ...
, which appeared in ''Zeitschrift für Physik
''Zeitschrift für Physik'' (English: ''Journal for Physics'') is a defunct series of German peer-reviewed physics journals established in 1920 by Springer Berlin Heidelberg. The series ended publication in 1997, when it merged with other journal ...
'' in September 1925.
In the article, Heisenberg tried to explain the energy levels of a one-dimensional anharmonic oscillator, avoiding the concrete but unobservable representations of electron orbits by using observable parameters such as transition probabilities for quantum jumps, which necessitated using two indexes corresponding to the initial and final states.
Mathematically, Heisenberg showed the need of non-commutative operators. This insight would later become the basis for Heisenberg's uncertainty principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position a ...
.
This article was followed by the paper by Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German-British theoretical physicist who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics, and supervised the work of a ...
and Pascual Jordan
Ernst Pascual Jordan (; 18 October 1902 – 31 July 1980) was a German theoretical and mathematical physicist who made significant contributions to quantum mechanics and quantum field theory. He contributed much to the mathematical form of matri ...
of the same year, and by the 'three-man paper' () by Born, Heisenberg and Jordan in 1926. These articles laid the groundwork for matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925. It was the first conceptually autonomous and logically consistent formulation of quantum mechanics. Its account of quantum ...
that would come to substitute old quantum theory
The old quantum theory is a collection of results from the years 1900–1925, which predate modern quantum mechanics. The theory was never complete or self-consistent, but was instead a set of heuristic corrections to classical mechanics. The th ...
, leading to the modern quantum mechanics. Heisenberg received the Nobel Prize in Physics
The Nobel Prize in Physics () is an annual award given by the Royal Swedish Academy of Sciences for those who have made the most outstanding contributions to mankind in the field of physics. It is one of the five Nobel Prizes established by the ...
in 1932 for his work on developing quantum mechanics.
Historical context
Heisenberg was 23 years old when he worked on the article while recovering fromhay fever
Allergic rhinitis, of which the seasonal type is called hay fever, is a type of rhinitis, inflammation in the nose that occurs when the immune system overreacts to allergens in the air. It is classified as a Allergy, type I hypersensitivity re ...
on the island of Heligoland
Heligoland (; , ; Heligolandic Frisian: , , Mooring Frisian: , ) is a small archipelago in the North Sea. The islands were historically possessions of Denmark, then became possessions of the United Kingdom from 1807 to 1890. Since 1890, the ...
, corresponding with Wolfgang Pauli
Wolfgang Ernst Pauli ( ; ; 25 April 1900 – 15 December 1958) was an Austrian theoretical physicist and a pioneer of quantum mechanics. In 1945, after having been nominated by Albert Einstein, Pauli received the Nobel Prize in Physics "for the ...
on the subject. When asked for his opinion of the manuscript, Pauli responded favorably, but Heisenberg said that he was still "very uncertain about it". In July 1925, he sent the manuscript to Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German-British theoretical physicist who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics, and supervised the work of a ...
to review and decide whether to submit it for publication.
When Born read the article, he recognized the formulation as one which could be transcribed and extended to the systematic language of matrices. Born, with the help of his assistant and former student Pascual Jordan, began immediately to make the transcription and extension, and they submitted their results for publication; their manuscript was received for publication just 60 days after Heisenberg’s article.M. Born and P. Jordan, ''Zur Quantenmechanik'', ''Zeitschrift für Physik'', 34, 858–888, 1925 (received September 27, 1925). nglish translation in: B. L. van der Waerden, editor, ''Sources of Quantum Mechanics''. Dover Publications, 1968. A follow-on article by all three authors extending the theory to multiple dimensions was submitted for publication before the end of the year.M. Born, W. Heisenberg, and P. Jordan, ''Zur Quantenmechanik II'', ''Zeitschrift für Physik'', 35, 557–615, 1925 (received November 16, 1925). nglish translation in: B. L. van der Waerden, editor, Sources of Quantum Mechanics. Dover Publications, 1968.
Heisenberg determined to base his quantum mechanics "exclusively upon relationships between quantities that in principle are observable". He observed that one could not then use any statements about such things as "the position and period of revolution of the electron". Rather, to make true progress in understanding the radiation of the simplest case, the radiation of excited hydrogen atoms, one had measurements only of the frequencies and the intensities of the hydrogen bright-line spectrum to work with.classical physics
Classical physics refers to physics theories that are non-quantum or both non-quantum and non-relativistic, depending on the context. In historical discussions, ''classical physics'' refers to pre-1900 physics, while '' modern physics'' refers to ...
, the intensity of each frequency of light produced in a radiating system is equal to the square of the amplitude of the radiation at that frequency, so attention next fell on amplitudes. The classical equations that Heisenberg hoped to use to form quantum theoretical equations would first yield the amplitudes, and in classical physics one could compute the intensities simply by squaring the amplitudes. But Heisenberg saw that "the simplest and most natural assumption would be" to follow the lead provided by recent work in computing light dispersion done by Hans Kramers
Hendrik Anthony "Hans" Kramers (17 December 1894 – 24 April 1952) was a Dutch physicist who worked with Niels Bohr to understand how electromagnetic waves interact with matter and made important contributions to quantum mechanics and statistica ...
. The work he had done assisting Kramers in the previous year now gave him an important clue about how to model what happened to excited hydrogen gas when it radiated light and what happened when incoming radiation of one frequency excited atoms in a dispersive medium and then the energy delivered by the incoming light was re-radiated sometimes at the original frequency but often at two lower frequencies the sum of which equalled the original frequency. According to their model, an electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
that had been driven to a higher energy state by accepting the energy of an incoming photon might return in one step to its equilibrium position, re-radiating a photon of the same frequency, or it might return in more than one step, radiating one photon for each step in its return to its equilibrium state. Because of the way factors cancel out in deriving the new equation based on these considerations, the result turns out to be relatively simple.
Also included in the manuscript was the ''Heisenberg commutator'', his law of multiplication needed to describe certain properties of atoms, whereby the product of two physical quantities did not commute. Therefore, ''PQ'' would differ from ''QP'' where, for example, ''P'' was an electron's momentum, and ''Q'' its position. Paul Dirac
Paul Adrien Maurice Dirac ( ; 8 August 1902 – 20 October 1984) was an English mathematician and Theoretical physics, theoretical physicist who is considered to be one of the founders of quantum mechanics. Dirac laid the foundations for bot ...
, who had received a proof copy in August 1925, realized that the commutative law had not been fully developed, and he produced an algebraic formulation to express the same results in more logical form.
Heisenberg's multiplication rule
 By means of an intense series of mathematical analogies that some physicists have termed "magical", Heisenberg wrote out an equation that is the quantum mechanical analog for the classical computation of intensities:
This general format indicates that some term is to be computed by summing up all of the products of some group of terms by some related group of terms . There will potentially be an infinite series of terms and their matching terms. Each of these multiplications has as its factors two measurements that pertain to sequential downward transitions between energy states of an electron. This type of rule differentiates matrix mechanics from the kind of physics familiar in everyday life because the important values are where (in what energy state or "orbital") the electron begins and in what energy state it ends, not what the electron is doing while in one or another state.
If and both refer to lists of frequencies, for instance, the calculation proceeds as follows:
Multiply the frequency for a change of energy from state to state by the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'', and to that add the product found by multiplying the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'' by the frequency for a change of energy from state ''n'' − ''b'' to state ''n'' − ''c'', and so forth. Symbolically, that is:
:
(According to the convention used, represents a higher energy state than , so a transition from to would indicate that an electron has accepted energy from an incoming photon and has risen to a higher orbital, while a transition from to would represent an electron falling to a lower orbital and emitting a photon.)
It would be easy to perform each individual step of this process for some measured quantity. For instance, the boxed formula at the head of this article gives each needed wavelength in sequence. The values calculated could very easily be filled into a grid as described below. However, since the series is infinite, nobody could do the entire set of calculations.
Heisenberg originally devised this equation to enable himself to multiply two measurements of the same kind (amplitudes), so it happened not to matter in which order they were multiplied. Heisenberg noticed, however that if he tried to use the same schema to multiply two variables, such as momentum, ''p'', and displacement, ''q'', then "a significant difficulty arises". It turns out that multiplying a matrix of ''p'' by a matrix of ''q'' gives a different result from multiplying a matrix of ''q'' by a matrix of ''p''. It only made a tiny bit of difference, but that difference could never be reduced below a certain limit, and that limit involved the
By means of an intense series of mathematical analogies that some physicists have termed "magical", Heisenberg wrote out an equation that is the quantum mechanical analog for the classical computation of intensities:
This general format indicates that some term is to be computed by summing up all of the products of some group of terms by some related group of terms . There will potentially be an infinite series of terms and their matching terms. Each of these multiplications has as its factors two measurements that pertain to sequential downward transitions between energy states of an electron. This type of rule differentiates matrix mechanics from the kind of physics familiar in everyday life because the important values are where (in what energy state or "orbital") the electron begins and in what energy state it ends, not what the electron is doing while in one or another state.
If and both refer to lists of frequencies, for instance, the calculation proceeds as follows:
Multiply the frequency for a change of energy from state to state by the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'', and to that add the product found by multiplying the frequency for a change of energy from state ''n'' − ''a'' to state ''n'' − ''b'' by the frequency for a change of energy from state ''n'' − ''b'' to state ''n'' − ''c'', and so forth. Symbolically, that is:
:
(According to the convention used, represents a higher energy state than , so a transition from to would indicate that an electron has accepted energy from an incoming photon and has risen to a higher orbital, while a transition from to would represent an electron falling to a lower orbital and emitting a photon.)
It would be easy to perform each individual step of this process for some measured quantity. For instance, the boxed formula at the head of this article gives each needed wavelength in sequence. The values calculated could very easily be filled into a grid as described below. However, since the series is infinite, nobody could do the entire set of calculations.
Heisenberg originally devised this equation to enable himself to multiply two measurements of the same kind (amplitudes), so it happened not to matter in which order they were multiplied. Heisenberg noticed, however that if he tried to use the same schema to multiply two variables, such as momentum, ''p'', and displacement, ''q'', then "a significant difficulty arises". It turns out that multiplying a matrix of ''p'' by a matrix of ''q'' gives a different result from multiplying a matrix of ''q'' by a matrix of ''p''. It only made a tiny bit of difference, but that difference could never be reduced below a certain limit, and that limit involved the Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
, ''h''. More on that later. Below is a very short sample of what the calculations would be, placed into grids that are called matrices. Heisenberg's teacher saw almost immediately that his work should be expressed in a matrix format because mathematicians already were familiar with how to do computations involving matrices in an efficient way. (Since Heisenberg was interested in photon radiation, the illustrations will be given in terms of electrons going from a higher energy level to a lower level, e.g., , instead of going from a lower level to a higher level, e.g., .)
(equation for the conjugate variables
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty relation— ...
momentum and position)
Matrix of ''p''
Matrix of ''q''
The matrix for the product of the above two matrices as specified by the relevant equation in the ''Umdeutung'' paper is
where
and so forth.
If the matrices were reversed, the following values would result
and so forth.
Development of matrix mechanics
 Werner Heisenberg used the idea that since classical physics is correct when it applies to phenomena in the world of things larger than atoms and molecules, it must stand as a special case of a more inclusive quantum theoretical model. So he hoped that he could modify quantum physics in such a way that when the parameters were on the scale of everyday objects it would look just like classical physics, but when the parameters were pulled down to the atomic scale the discontinuities seen in things like the widely spaced frequencies of the visible hydrogen bright line spectrum would come back into sight.
The one thing that people at that time most wanted to understand about hydrogen radiation was how to predict or account for the intensities of the lines in its spectrum. Although Heisenberg did not know it at the time, the general format he worked out to express his new way of working with quantum theoretical calculations can serve as a recipe for two matrices and how to multiply them.
The ''Umdeutung'' paper does not mention matrices. Heisenberg's great advance was the "scheme which was capable in principle of determining uniquely the relevant physical qualities (transition frequencies and amplitudes)" of hydrogen radiation.
After Heisenberg wrote the ''Umdeutung'' paper, he turned it over to one of his senior colleagues for any needed corrections and went on vacation.
Werner Heisenberg used the idea that since classical physics is correct when it applies to phenomena in the world of things larger than atoms and molecules, it must stand as a special case of a more inclusive quantum theoretical model. So he hoped that he could modify quantum physics in such a way that when the parameters were on the scale of everyday objects it would look just like classical physics, but when the parameters were pulled down to the atomic scale the discontinuities seen in things like the widely spaced frequencies of the visible hydrogen bright line spectrum would come back into sight.
The one thing that people at that time most wanted to understand about hydrogen radiation was how to predict or account for the intensities of the lines in its spectrum. Although Heisenberg did not know it at the time, the general format he worked out to express his new way of working with quantum theoretical calculations can serve as a recipe for two matrices and how to multiply them.
The ''Umdeutung'' paper does not mention matrices. Heisenberg's great advance was the "scheme which was capable in principle of determining uniquely the relevant physical qualities (transition frequencies and amplitudes)" of hydrogen radiation.
After Heisenberg wrote the ''Umdeutung'' paper, he turned it over to one of his senior colleagues for any needed corrections and went on vacation. Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German-British theoretical physicist who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics, and supervised the work of a ...
puzzled over the equations and the non-commuting equations that Heisenberg had found troublesome and disturbing. After several days he realized that these equations amounted to directions for writing out matrices.
By consideration of ... examples. .. eisenbergfound this rule ... This was in the summer of 1925. Heisenberg ... took leave of absence ... and handed over his paper to me for publication ... Heisenberg's rule of multiplication left me no peace, and after a week of intensive thought and trial, I suddenly remembered an algebraic theory....Such quadratic arrays are quite familiar to mathematicians and are called matrices, in association with a definite rule of multiplication. I applied this rule to Heisenberg's quantum condition and found that it agreed for the diagonal elements. It was easy to guess what the remaining elements must be, namely, null; and immediately there stood before me the strange formulaThe symbol ''Q'' is the matrix for displacement, ''P'' is the matrix for momentum, stands for the square root of negative one, and is the Planck constant. Born and a few colleagues took up the task of working everything out in matrix form before Heisenberg returned from his time off, and within a few months the new quantum mechanics in matrix form formed the basis for another paper. This relation is now known as Heisenberg's
uncertainty principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position a ...
.
When quantities such as position and momentum are mentioned in the context of Heisenberg's matrix mechanics, a statement such as ''pq'' ≠''qp'' does not refer to a single value of ''p'' and a single value ''q'' but to a matrix (grid of values arranged in a defined way) of values of position and a matrix of values of momentum. So multiplying ''p'' times ''q'' or ''q'' times ''p'' is really talking about the matrix multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the n ...
of the two matrices. When two matrices are multiplied, the answer is a third matrix.
Paul Dirac
Paul Adrien Maurice Dirac ( ; 8 August 1902 – 20 October 1984) was an English mathematician and Theoretical physics, theoretical physicist who is considered to be one of the founders of quantum mechanics. Dirac laid the foundations for bot ...
decided that the essence of Heisenberg's work lay in the very feature that Heisenberg had originally found problematical the fact of non-commutativity such as that between multiplication of a momentum matrix by a displacement matrix and multiplication of a displacement matrix by a momentum matrix. That insight led Dirac in new and productive directions.Thomas F. Jordan, ''Quantum Mechanics in Simple Matrix Form'', p. 149
See also
*History of quantum mechanics
The history of quantum mechanics is a fundamental part of the History of physics#20th century: birth of modern physics, history of modern physics. The major chapters of this history begin with the emergence of quantum ideas to explain individual ...
* Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, whic ...
References
Further reading
* * An English translatio"Quantum-theoretical reinterpretation of kinematic and mechanical relations"
by B. L. van der Waerden may be found in * The crucial reinterpretation synthesis of Heisenberg's paper, which introduces the contemporary language employed now. {{DEFAULTSORT:Ueber quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen Historical physics publications 1925 in science 1925 documents 1925 in Germany Physics papers Works originally published in German magazines Works originally published in science and technology magazines Werner Heisenberg