|
ÎĽ Operator
In computability theory, the μ-operator, minimization operator, or unbounded search operator searches for the least natural number with a given property. Adding the μ-operator to the primitive recursive functions makes it possible to define all computable functions. Definition Suppose that R(''y'', ''x''1, ..., ''x''''k'') is a fixed (''k''+1)-ary relation on the natural numbers. The μ-operator "μ''y''", in either the unbounded or bounded form, is a " number theoretic function" defined from the natural numbers to the natural numbers. However, "μ''y''" contains a '' predicate'' over the natural numbers, which can be thought of as a condition that evaluates to ''true'' when the predicate is satisfied and ''false'' when it is not. The ''bounded'' μ-operator appears earlier in Kleene (1952) ''Chapter IX Primitive Recursive Functions, §45 Predicates, prime factor representation'' as: :"\mu y_ R(y). \ \ \mbox \ y [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursion Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definable set, definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function (mathematics), function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of computational complexity theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive Functions
In computability theory, a primitive recursive function is, roughly speaking, a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop is fixed before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not particularly easy to devise a computable function that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
While Loop
In most computer programming languages, a while loop is a control flow Statement (computer science), statement that allows code to be executed repeatedly based on a given Boolean data type, Boolean condition. The ''while'' loop can be thought of as a repeating Conditional (computer programming), if statement. Overview The ''while'' construct consists of a block of code and a condition/expression. The condition/expression is evaluated, and if the condition/expression is ''true'', the code within all of their following in the block is executed. This repeats until the condition/expression becomes False (logic), false. Because the ''while'' loop checks the condition/expression before the block is executed, the control structure is often also known as a pre-test loop. Compare this with the do while loop, ''do while'' loop, which tests the condition/expression ''after'' the loop has executed. For example, in the languages C (programming language), C, Java (programming language), Java ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peano Axioms
In mathematical logic, the Peano axioms (, ), also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th-century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete. The axiomatization of arithmetic provided by Peano axioms is commonly called Peano arithmetic. The importance of formalizing arithmetic was not well appreciated until the work of Hermann Grassmann, who showed in the 1860s that many facts in arithmetic could be derived from more basic facts about the successor operation and induction. In 1881, Charles Sanders Peirce provided an axiomatization of natural-number arithmetic. In 1888, Richard Dedekind proposed another axiomatization of natural-number arithmetic, and in 1889, Peano published a simplified version of them as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternative Abstract Machine Models Of The Unbounded
Alternative or alternate may refer to: Arts, entertainment and media * Alternative (''Kamen Rider''), a character in the Japanese TV series ''Kamen Rider Ryuki'' * Alternative comics, or independent comics are an alternative to mainstream superhero comics * Alternative fashion, fashion that stands apart from mainstream, commercial fashion. * Alternative manga, manga published outside the more commercial market, or which have different art styles, themes, and narratives to those found in the more popular manga magazines. * '' AlterNative'', academic journal * ''The Alternative'' (film), a 1978 Australian television film * ''The Alternative'', a radio show hosted by Tony Evans * ''120 Minutes'' (2004 TV program), an alternative rock music video program formerly known as ''The Alternative'' *'' The American Spectator'', an American magazine formerly known as ''The Alternative: An American Spectator'' Music * Alternative dance, a musical genre that mixes alternative rock with el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counter Machine
A counter machine or counter automaton is an abstract machine used in a formal logic and theoretical computer science to model computation. It is the most primitive of the four types of register machines. A counter machine comprises a set of one or more unbounded ''registers'', each of which can hold a single non-negative integer, and a list of (usually sequential) arithmetic and control instructions for the machine to follow. The counter machine is typically used in the process of designing parallel algorithms in relation to the mutual exclusion principle. When used in this manner, the counter machine is used to model the discrete time-steps of a computational system in relation to memory accesses. By modeling computations in relation to the memory accesses for each respective computational step, parallel algorithms may be designed in such a matter to avoid interlocking, the simultaneous writing operation by two (or more) threads to the same memory address. Counter machines wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing-equivalent
Turing equivalence may refer to: * As related to Turing completeness, Turing equivalence means having computational power equivalent to a universal Turing machine * Turing degree In computer science and mathematical logic the Turing degree (named after Alan Turing) or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set. Overview The concept of Turing degree is fund ... equivalence (of sets), having the same level of unsolvability See also * Turing machine equivalents * Turing test (other) {{mathdab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
McCarthy Formalism
In computer science and recursion theory the McCarthy Formalism (1963) of computer scientist John McCarthy clarifies the notion of recursive functions by use of the IF-THEN-ELSE construction common to computer science, together with four of the operators of primitive recursive functions: zero, successor, equality of numbers and composition. The conditional operator replaces both primitive recursion and the mu-operator. Introduction McCarthy's notion of ''conditional expression'' McCarthy (1960) described his formalism this way: :"In this article, we first describe a formalism for defining functions recursively. We believe this formalism has advantages both as a programming language and as a vehicle for developing a theory of computation.... :We shall need a number of mathematical ideas and notations concerning functions in general. Most of the ideas are well known, but the notion of ''conditional expression'' is believed to be new, and the use of ''conditional expressions'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
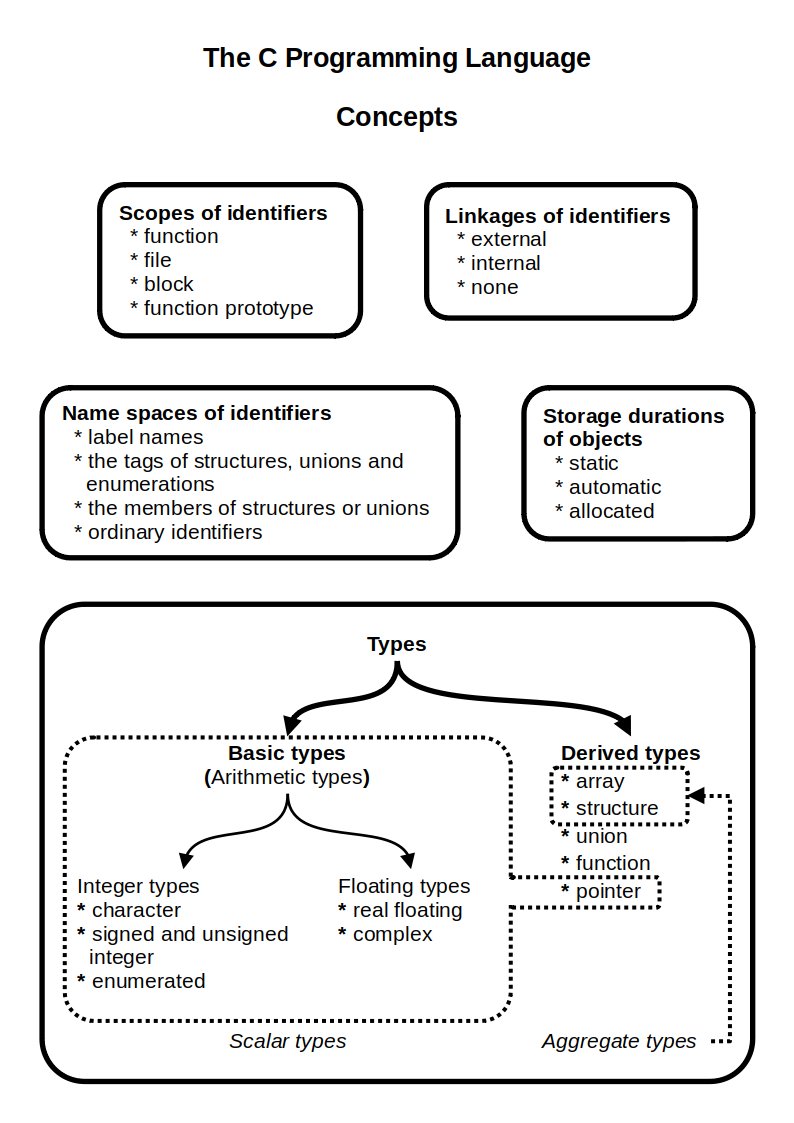
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Function Demonstration
Total may refer to: Mathematics * Total, the summation of a set of numbers * Total order, a partial order without incomparable pairs * Total relation, which may also mean ** connected relation (a binary relation in which any two elements are comparable). * Total function, a partial function that is also a total relation Business * TotalEnergies, a French petroleum company, formerly known as Total * Total (cereal), a food brand by General Mills * Total, a brand of strained yogurt made by Fage * Total, a database management system marketed by Cincom Systems * Total Linhas AĂ©reas, a Brazilian airline * Total, a line of dental products by Colgate Music and culture * Total (group), an American R&B girl group * '' Total: From Joy Division to New Order'', a compilation album * ''Total'' (Sebastian album) * ''Total'' (Total album) * ''Total'' (Teenage Bottlerocket album) * ''Total'' (Seigmen album) * ''Total'' (Wanessa album) * ''Total'' (Belinda PeregrĂn album) * ''Tot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov's Principle
Markov's principle (also known as the Leningrad principle), named after Andrey Markov Jr, is a conditional existence statement for which there are many equivalent formulations, as discussed below. The principle is logically valid classically, but not in intuitionistic constructive mathematics. However, many particular instances of it are nevertheless provable in a constructive context as well. History The principle was first studied and adopted by the Russian school of constructivism, together with choice principles and often with a realizability perspective on the notion of mathematical function. In computability theory In the language of computability theory, Markov's principle is a formal expression of the claim that if it is impossible that an algorithm does not terminate, then for some input it does terminate. This is equivalent to the claim that if a set and its complement are both computably enumerable, then the set is decidable. These statements are provable in cla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructive Mathematics
In the philosophy of mathematics, constructivism asserts that it is necessary to find (or "construct") a specific example of a mathematical object in order to prove that an example exists. Contrastingly, in classical mathematics, one can prove the existence of a mathematical object without "finding" that object explicitly, by assuming its non-existence and then deriving a contradiction from that assumption. Such a proof by contradiction might be called non-constructive, and a constructivist might reject it. The constructive viewpoint involves a verificational interpretation of the existential quantifier, which is at odds with its classical interpretation. There are many forms of constructivism. These include the program of intuitionism founded by Luitzen Egbertus Jan Brouwer, Brouwer, the finitism of David Hilbert, Hilbert and Paul Bernays, Bernays, the constructive recursive mathematics of Nikolai Aleksandrovich Shanin, Shanin and Andrey Markov (Soviet mathematician), Markov, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |