|
Wreath Product
In group theory, the wreath product is a special combination of two groups based on the semidirect product. It is formed by the action of one group on many copies of another group, somewhat analogous to exponentiation. Wreath products are used in the classification of permutation groups and also provide a way of constructing interesting examples of groups. Given two groups A and H (sometimes known as the ''bottom'' and ''top''), there exist two variations of the wreath product: the unrestricted wreath product A \text H and the restricted wreath product A \text H. The general form, denoted by A \text_ H or A \text_ H respectively, requires that H acts on some set \Omega; when unspecified, usually \Omega = H (a regular wreath product), though a different \Omega is sometimes implied. The two variations coincide when A, H, and \Omega are all finite. Either variation is also denoted as A \wr H (with \wr for the LaTeX symbol) or ''A'' ≀ ''H'' (Unicode U+2240). The notion ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
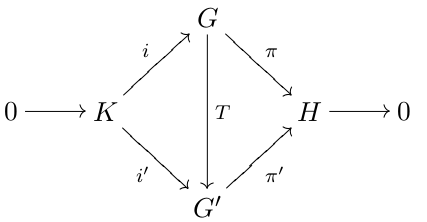
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree (data Structure)
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be connected to exactly one parent, except for the ''root'' node, which has no parent. These constraints mean there are no cycles or "loops" (no node can be its own ancestor), and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes in a single straight line. Binary trees are a commonly used type, which constrain the number of children for each parent to exactly two. When the order of the children is specified, this data structure corresponds to an ordered tree in graph theory. A value or pointer to other data may be associated with every node in the tre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Sudoku
The mathematics of Sudoku refers to the use of mathematics to study Sudoku puzzles to answer questions such as ''"How many filled Sudoku grids are there?"'', "''What is the minimal number of clues in a valid puzzle?''" and ''"In what ways can Sudoku grids be symmetric?"'' through the use of combinatorics and group theory. The analysis of Sudoku falls is generally divided between analyzing the properties of unsolved puzzles (such as the minimum possible number of given clues) and analyzing the properties of solved puzzles. Initial analysis was largely focused on enumerating solutions, with results first appearing in 2004. For classical Sudoku, the number of filled grids is 6,670,903,752,021,072,936,960 (), which reduces to 5,472,730,538 essentially different solutions under the validity preserving transformations. There are 26 types of symmetry, but they can only be found in about 0.005% of all filled grids. A puzzle with a unique solution must have at least 17 clues, and there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rubik's Cube Group
The Rubik's Cube group is a Group (mathematics), group (G, \cdot ) that represents the Mathematical structure, structure of the Rubik's Cube mechanical puzzle. Each element of the Set (mathematics), set G corresponds to a cube move, which is the effect of any sequence of rotations of the cube's faces. With this representation, not only can any cube move be represented, but also any position of the cube as well, by detailing the cube moves required to rotate the solved cube into that position. Indeed with the solved position as a starting point, there is a Bijection, one-to-one correspondence between each of the legal positions of the Rubik's Cube and the elements of G. The group Binary operation, operation \cdot is the Function composition, composition of cube moves, corresponding to the result of performing one cube move after another. The Rubik's Cube group is constructed by labeling each of the 48 non-center facets with the integers 1 to 48. Each configuration of the cube ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annales Scientifiques De L'École Normale Supérieure
''Annales Scientifiques de l'École Normale Supérieure'' is a French scientific journal of mathematics published by the Société Mathématique de France. It was established in 1864 by the French chemist Louis Pasteur and published articles in mathematics, physics, chemistry, biology, and geology. In 1900, it became a purely mathematical journal. It is published with help of the Centre national de la recherche scientifique. Its web site is hosted by the mathematics department of the École Normale Supérieure École may refer to: * an elementary school in the French educational stages normally followed by secondary education establishments (collège and lycée) * École (river), a tributary of the Seine flowing in région Île-de-France * École, Savoi .... External links * Archive(1864–2013) Mathematics journals Publications established in 1864 Multilingual journals Multidisciplinary scientific journals Société Mathématique de France academic journals {{mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylow Theorems
In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups. For a prime number p, a Sylow ''p''-subgroup (sometimes ''p''-Sylow subgroup) of a group G is a maximal p-subgroup of G, i.e., a subgroup of G that is a ''p''-group (meaning its cardinality is a power of p, or equivalently, the order of every group element is a power of p) that is not a proper subgroup of any other p-subgroup of G. The set of all Sylow p-subgroups for a given prime p is sometimes written \text_p(G). The Sylow theorems assert a partial converse to Lagrange's theorem. Lagrange's theorem states that for any finite group G the order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
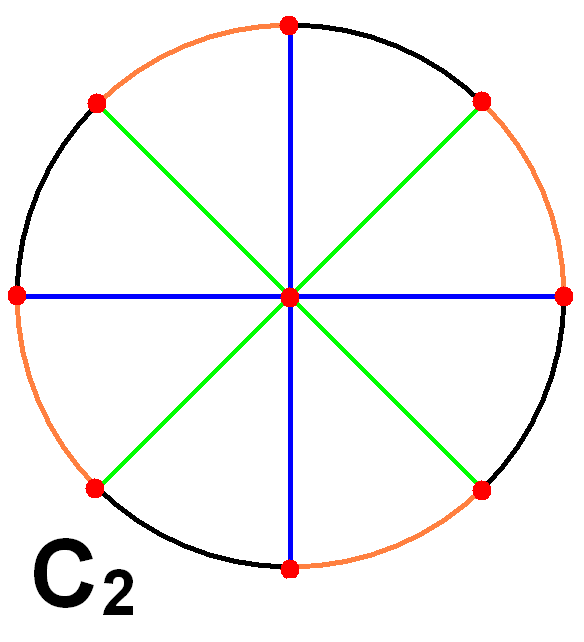
Dihedral Group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetries and n reflection symmetries. Usually, we take n \ge 3 here. The associated rotations and reflections make up the dihedral group \mathrm_n. If n is odd, each axis of symmetry connects the midpoint of one side to the opposite vertex. If n is even, there are n/2 axes of symmetry connecting the midpoints of opposite sides and n/2 axes of symmetry connecting oppo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic. From the standpoint of group theory, isomorphic groups have the same properties and need not be distinguished. Definition and notation Given two groups (G, *) and (H, \odot), a ''group isomorphism'' from (G, *) to (H, \odot) is a bijective group homomorphism from G to H. Spelled out, this means that a group isomorphism is a bijective function f : G \to H such that for all u and v in G it holds that f(u * v) = f(u) \odot f(v). The two groups (G, *) and (H, \odot) are isomorphic if there exists an isomorphism from one to the other. This is written (G, *) \cong (H, \odot). Often shorter and simpler notations can be used. When the relevant group operations are understood, they are omitted and one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperoctahedral Group
In mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. It was named by Alfred Young in 1930. Groups of this type are identified by a parameter , the dimension of the hypercube. As a Coxeter group it is of type , and as a Weyl group it is associated to the symplectic groups and with the orthogonal groups in odd dimensions. As a wreath product it is S_2 \wr S_n where is the symmetric group of degree . As a permutation group, the group is the signed symmetric group of permutations ''π'' either of the set or of the set such that for all . As a matrix group, it can be described as the group of orthogonal matrices whose entries are all integers. Equivalently, this is the set of matrices with entries only 0, 1, or –1, which are invertible, and which have exactly one non-zero entry in each row or column. The representation theory of the hyperoctahedral grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Symmetric Group
In mathematics, the generalized symmetric group is the wreath product S(m,n) := Z_m \wr S_n of the cyclic group of order ''m'' and the symmetric group of order ''n''. Examples * For m=1, the generalized symmetric group is exactly the ordinary symmetric group: S(1,n) = S_n. * For m=2, one can consider the cyclic group of order 2 as positives and negatives (Z_2 \cong \) and identify the generalized symmetric group S(2,n) with the signed symmetric group. Representation theory There is a natural representation of elements of S(m,n) as generalized permutation matrices, where the nonzero entries are ''m''-th roots of unity: Z_m \cong \mu_m. The representation theory has been studied since ; see references in . As with the symmetric group, the representations can be constructed in terms of Specht modules; see . Homology The first group homology group (concretely, the abelianization) is Z_m \times Z_2 (for ''m'' odd this is isomorphic to Z_): the Z_m factors (which are all conj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)