|
Wave Height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighboring trough. ''Wave height'' is a term used by mariners, as well as in coastal, ocean and naval engineering. At sea, the term ''significant wave height'' is used as a means to introduce a well-defined and standardized statistic to denote the characteristic height of the random waves in a '' sea state'', including wind sea and swell. It is defined in such a way that it more or less corresponds to what a mariner observes when estimating visually the average wave height. Definitions Depending on context, wave height may be defined in different ways: *For a sine wave, the wave height ''H'' is twice the amplitude (i.e., the '' peak-to-peak amplitude''): H = 2a. *For a periodic wave, it is simply the difference between the maximum and minimum of the surface elevation : H = \max\left\ - \min\left\, with ''c''p the phase speed (or propagation speed) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Water Waves
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the '' fetch''. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over high, being limited by wind speed, duration, fetch, and water depth. When directly generated and affected by local wind, a wind wave system is called a wind sea. Wind waves will travel in a great circle route after being generated – curving slightly left in the southern hemisphere and slightly right in the northern hemisphere. After moving out of the area of fetch and no longer being affected by the local wind, wind waves are called '' swells'' and can travel thousands of kilometers. A noteworthy example of this is waves generated south of Tasmania during heavy win ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significant Wave Height
In physical oceanography, the significant wave height (SWH, HTSGW or ''H''s) is defined traditionally as the mean ''wave height'' (trough (physics), trough to crest (physics), crest) of the highest third of the ocean surface wave, waves (''H''1/3). It is usually defined as four times the standard deviation of the surface elevation – or equivalently as four times the square root of the zeroth-order moment (area) of the ''wave spectrum''. The symbol ''H''m0 is usually used for that latter definition. The significant wave height (Hs) may thus refer to ''H''m0 or ''H''1/3; the difference in magnitude between the two definitions is only a few percent. SWH is used to characterize ''sea state'', including winds and swell (ocean), swell. Origin and definition The original definition resulted from work by the oceanographer Walter Munk during World War II. The significant wave height was intended to mathematically express the height estimated by a "trained observer". It is commonly used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
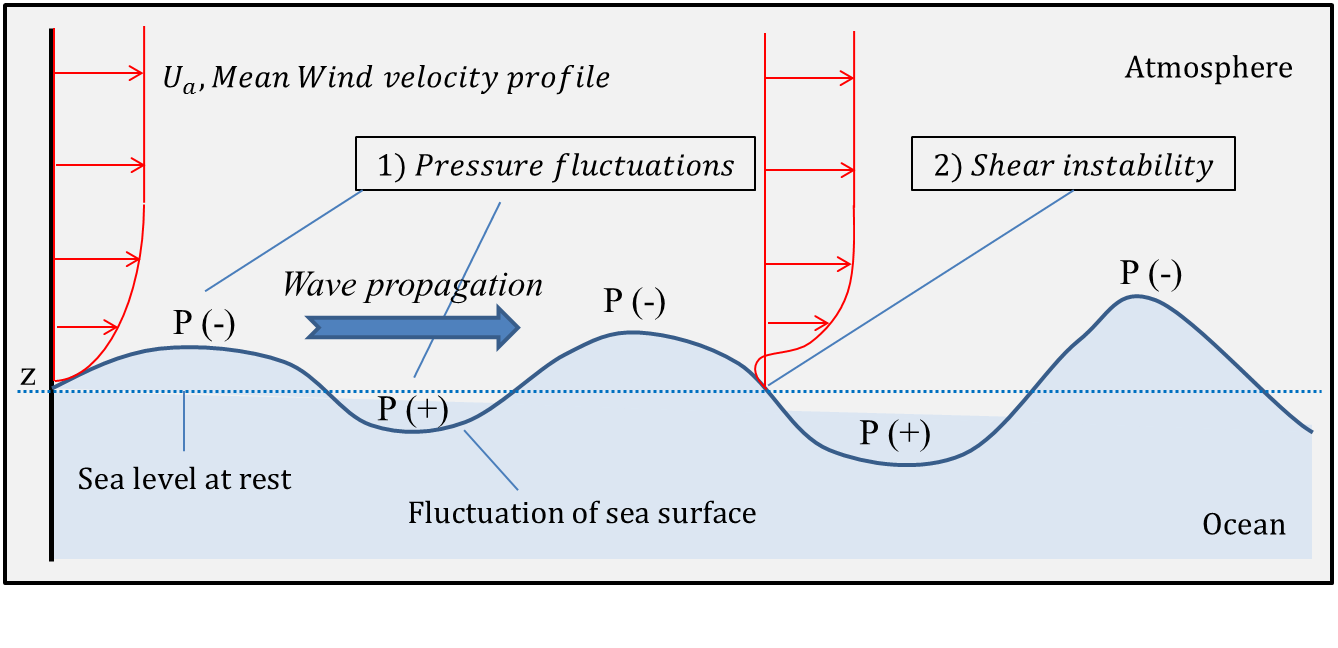
Ocean Surface Wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of Body of water, bodies of water as a result of the wind blowing over the water's surface. The contact distance in the wind direction, direction of the wind is known as the ''Wind fetch, fetch''. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small capillary wave, ripples to waves over high, being limited by wind speed, duration, fetch, and water depth. When directly generated and affected by local wind, a wind wave system is called a wind sea. Wind waves will travel in a great circle route after being generated – curving slightly left in the southern hemisphere and slightly right in the northern hemisphere. After moving out of the area of fetch and no longer being affected by the local wind, wind waves are called ''swell (ocean), swells'' and can travel thousands of kilometers. A noteworthy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind Wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is known as the '' fetch''. Waves in the oceans can travel thousands of kilometers before reaching land. Wind waves on Earth range in size from small ripples to waves over high, being limited by wind speed, duration, fetch, and water depth. When directly generated and affected by local wind, a wind wave system is called a wind sea. Wind waves will travel in a great circle route after being generated – curving slightly left in the southern hemisphere and slightly right in the northern hemisphere. After moving out of the area of fetch and no longer being affected by the local wind, wind waves are called '' swells'' and can travel thousands of kilometers. A noteworthy example of this is waves generated south of Tasmania during heavy wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum
In mathematical analysis, the maximum and minimum of a function (mathematics), function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given Interval (mathematics), range (the ''local'' or ''relative'' extrema) or on the entire domain of a function, domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set (mathematics), set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued Function (mathematics), function ''f'' defined on a Domain of a function, domain ''X'' has a global (or absolute) m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative'' extrema) or on the entire domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Speed
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength (lambda) and time period as :v_\mathrm = \frac. Equivalently, in terms of the wave's angular frequency , which specifies angular change per unit of time, and wavenumber (or angular wave number) , which represent the angular change per unit of space, :v_\mathrm = \frac. To gain some basic intuition for this equation, we consider a propagating (cosine) wave . We want to see how fast a particular phase of the wave travels. For example, we can choose , the phase of the first crest. This implies , and so . Formally, we let the phase and see immediately that and . So, it immediately follows that : \frac = -\frac \frac = \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weather Buoy
Weather buoys are instruments which collect weather and ocean data within the world's oceans, as well as aid during emergency response to chemical spills, legal proceedings, and engineering design. Moored buoys have been in use since 1951, while drifting buoys have been used since 1979. Moored buoys are connected with the ocean bottom using either chains, nylon, or buoyant polypropylene. With the decline of the weather ship, they have taken a more primary role in measuring conditions over the open seas since the 1970s. During the 1980s and 1990s, a network of buoys in the central and eastern tropical Pacific Ocean helped study the El Niño-Southern Oscillation. Moored weather buoys range from in diameter, while drifting buoys are smaller, with diameters of . Drifting buoys are the dominant form of weather buoy in sheer number, with 1250 located worldwide. Wind data from buoys has smaller error than that from ships. There are differences in the values of sea surface tempe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peak-to-peak Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude and semi-amplitude For symmetric periodic waves, like sine waves or triangle waves, ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the measurand is a signal that swings above and below a reference value but is not sinusoidal, peak amplitude is often used. If the reference is zero, this is the maximum absolute value of the signal; if the reference is a mean value (DC component), the peak amplitude is the maximum absolute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |