|
Vine Copula
A vine is a graphical tool for labeling constraints in high-dimensional probability distributions. A regular vine is a special case for which all constraints are two-dimensional or conditional two-dimensional. Regular vines generalize trees, and are themselves specializations of Cantor tree. Combined with bivariate copulas, regular vines have proven to be a flexible tool in high-dimensional dependence modeling. Copulas are multivariate distributions with uniform univariate margins. Representing a joint distribution as univariate margins plus copulas allows the separation of the problems of estimating univariate distributions from the problems of estimating dependence. This is handy in as much as univariate distributions in many cases can be adequately estimated from data, whereas dependence information is rough known, involving summary indicators and judgment. Although the number of parametric multivariate copula families with flexible dependence is limited, there are many parametr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cantor Tree
In mathematical set theory, the Cantor tree is either the full binary tree of height ω + 1, or a topological space related to this by joining its points with intervals, that was introduced by Robert Lee Moore in the late 1920s as an example of a non-metrizable Moore space . References * * *{{Citation , last1=Steen , first1=Lynn Arthur , author1-link=Lynn Arthur Steen , last2=Seebach , first2=J. Arthur Jr. , author2-link=J. Arthur Seebach, Jr. , title=Counterexamples in Topology , origyear=1978 , publisher=Springer-Verlag , location=Berlin, New York , edition=Dover Dover () is a town and major ferry port in Kent, South East England. It faces France across the Strait of Dover, the narrowest part of the English Channel at from Cap Gris Nez in France. It lies south-east of Canterbury and east of Maidstone ... reprint of 1978 , isbn=978-0-486-68735-3 , mr=507446 , year=1995 Trees (set theory) Topological spaces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Copula (probability Theory)
In probability theory and statistics, a copula is a multivariate cumulative distribution function for which the marginal probability distribution of each variable is uniform on the interval , 1 Copulas are used to describe/model the dependence (inter-correlation) between random variables. Their name, introduced by applied mathematician Abe Sklar in 1959, comes from the Latin for "link" or "tie", similar but unrelated to grammatical copulas in linguistics. Copulas have been used widely in quantitative finance to model and minimize tail risk and portfolio-optimization applications. Sklar's theorem states that any multivariate joint distribution can be written in terms of univariate marginal distribution functions and a copula which describes the dependence structure between the variables. Copulas are popular in high-dimensional statistical applications as they allow one to easily model and estimate the distribution of random vectors by estimating marginals and copulae ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Networks
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases. Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (''e.g.'' speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams. Graphical mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Correlation
In probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed. When determining the numerical relationship between two variables of interest, using their correlation coefficient will give misleading results if there is another confounding variable that is numerically related to both variables of interest. This misleading information can be avoided by controlling for the confounding variable, which is done by computing the partial correlation coefficient. This is precisely the motivation for including other right-side variables in a multiple regression; but while multiple regression gives unbiased results for the effect size, it does not give a numerical value of a measure of the strength of the relationship between the two variables of interest. For example, given economic data on the consumption, income, and wealth of various individuals, consider the rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphical Model
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a Graph (discrete mathematics), graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning. Types of graphical models Generally, probabilistic graphical models use a graph-based representation as the foundation for encoding a distribution over a multi-dimensional space and a graph that is a compact or Factor graph, factorized representation of a set of independences that hold in the specific distribution. Two branches of graphical representations of distributions are commonly used, namely, Bayesian networks and Markov random fields. Both families encompass the properties of factorization and independences, but they differ in the set of independences they can encode and the factorization of the distribution that they induce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
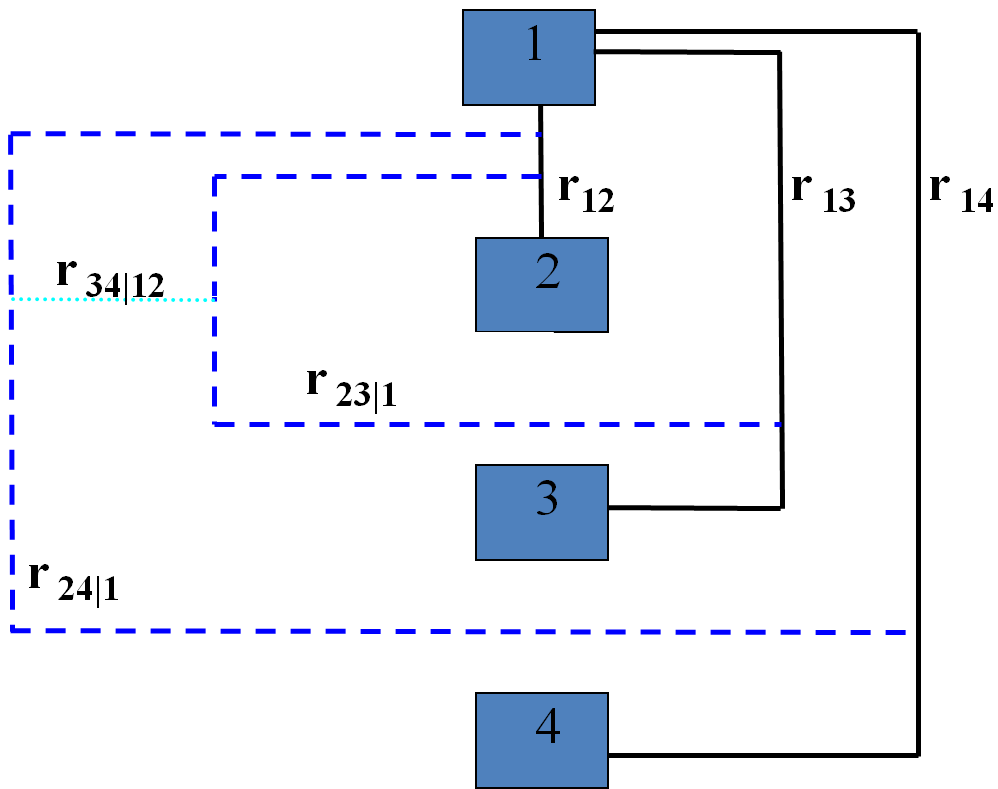
Regular Vine On 5 Variables
The term regular can mean normal or in accordance with rules. It may refer to: People * Moses Regular (born 1971), America football player Arts, entertainment, and media Music * "Regular" (Badfinger song) * Regular tunings of stringed instruments, tunings with equal intervals between the paired notes of successive open strings Other uses in arts, entertainment, and media * Regular character, a main character who appears more frequently and/or prominently than a recurring character * Regular division of the plane, a series of drawings by the Dutch artist M. C. Escher which began in 1936 * ''Regular Show'', an animated television sitcom * '' The Regular Guys'', a radio morning show Language * Regular inflection, the formation of derived forms such as plurals in ways that are typical for the language ** Regular verb * Regular script, the newest of the Chinese script styles Mathematics There are an extremely large number of unrelated notions of "regularity" in mathematics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and Y. MI is the expected value of the pointwise mutual information (PMI). The quantity was defined and analyzed by Claude Shannon in his landmark paper "A Mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence (probability Theory)
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |