|
Unit Fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/''n''. Examples are 1/1, 1/2, 1/3, 1/4, 1/5, etc. Arithmetic Elementary arithmetic Multiplying any two unit fractions results in a product that is another unit fraction: \frac1x \times \frac1y = \frac1. However, adding, subtracting, or dividing two unit fractions produces a result that is generally not a unit fraction: \frac1x + \frac1y = \frac \frac1x - \frac1y = \frac \frac1x \div \frac1y = \frac. Modular arithmetic In modular arithmetic, unit fractions can often be converted into equivalent integers using a calculation based on greatest common divisors. In turn, this conversion can be used to simplify division operations in modular arithmetic, by transforming them into equivalent multiplication operations. Specifically, consider the problem of dividing by a value x modulo y. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface , or blackboard bold \mathbb. A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real number that is not rational is called irrational. Irrational numbers include , , , and . Since the set of rational numbers is countable, and the set of real numbers is uncountable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apéry's Constant
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number : \begin \zeta(3) &= \sum_^\infty \frac \\ &= \lim_ \left(\frac + \frac + \cdots + \frac\right), \end where is the Riemann zeta function. It has an approximate value of : . The constant is named after Roger Apéry. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics. It also arises in the analysis of random minimum spanning trees and in conjunction with the gamma function when solving certain integrals involving exponential functions in a quotient, which appear occasionally in physics, for instance, when evaluating the two-dimensional case of the Debye model and the Stefan–Boltzmann law. Irrational number was named ''Apéry's constant'' after the French mathematician Roger Apéry, who proved in 1978 that it is an ir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basel Problem
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in ''The Saint Petersburg Academy of Sciences''. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up years later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem. The Basel problem asks for the precise summation of the reciprocals of the squares of the natural numbers, i.e. the precise sum of the infinite series: \sum_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz Formula For π
In mathematics, the Leibniz formula for , named after Gottfried Leibniz, states that 1-\frac+\frac-\frac+\frac-\cdots=\frac, an alternating series. It is also called the Madhava–Leibniz series as it is a special case of a more general series expansion for the inverse tangent function, first discovered by the Indian mathematician Madhava of Sangamagrama in the 14th century, the specific case first published by Leibniz around 1676. The series for the inverse tangent function, which is also known as Gregory's series, can be given by: : \arctan x = x - \frac + \frac - \frac + \cdots The Leibniz formula for \frac can be obtained by putting x=1 into this series. It also is the Dirichlet -series of the non-principal Dirichlet character of modulus 4 evaluated at s=1, and, therefore, the value of the Dirichlet beta function. Proofs Proof 1 \begin \frac &= \arctan(1) \\ &= \int_0^1 \frac 1 \, dx \\ pt& = \int_0^1\left(\sum_^n (-1)^k x^+\frac\right) \, dx \\ pt& = \left(\sum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm Of 2
The decimal value of the natural logarithm of 2 is approximately :\ln 2 \approx 0.693\,147\,180\,559\,945\,309\,417\,232\,121\,458. The logarithm of 2 in other bases is obtained with the formula :\log_b 2 = \frac. The common logarithm in particular is () :\log_ 2 \approx 0.301\,029\,995\,663\,981\,195. The inverse of this number is the binary logarithm of 10: : \log_2 10 =\frac \approx 3.321\,928\,095 (). By the Lindemann–Weierstrass theorem, the natural logarithm of any natural number other than 0 and 1 (more generally, of any positive algebraic number other than 1) is a transcendental number. Series representations Rising alternate factorial :\ln 2 = \sum_^\infty \frac=1-\frac12+\frac13-\frac14+\frac15-\frac16+\cdots. This is the well-known "alternating harmonic series". :\ln 2 = \frac +\frac\sum_^\infty \frac. :\ln 2 = \frac +\frac\sum_^\infty \frac. :\ln 2 = \frac +\frac\sum_^\infty \frac. :\ln 2 = \frac +\frac\sum_^\infty \frac. :\ln 2 = \frac +\frac\sum_^\infty \frac. : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term "natural". The definition of the natural logarithm can then b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
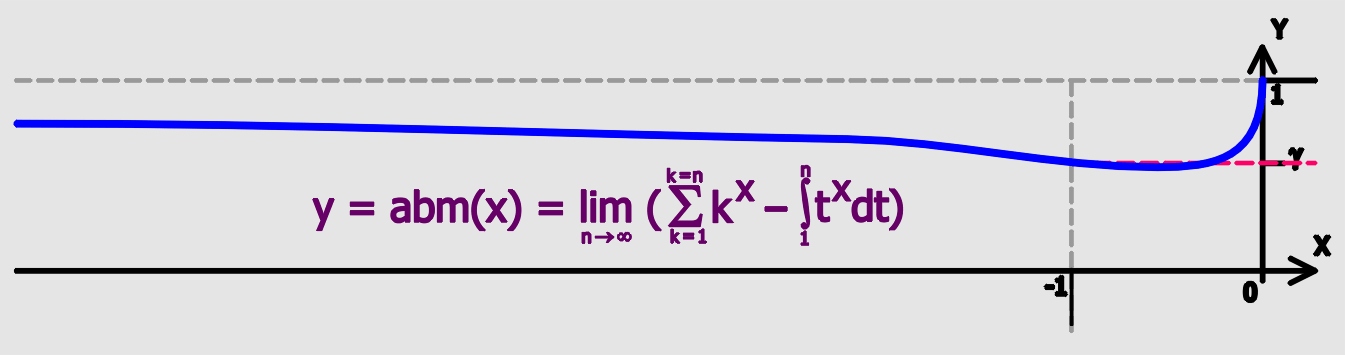
Harmonic Series (mathematics)
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions: \sum_^\infty\frac = 1 + \frac + \frac + \frac + \frac + \cdots. The first n terms of the series sum to approximately \ln n + \gamma, where \ln is the natural logarithm and \gamma\approx0.577 is the Euler–Mascheroni constant. Because the logarithm has arbitrarily large values, the harmonic series does not have a finite limit: it is a divergent series. Its divergence was proven in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to diverge by comparing the sum to an integral, according to the integral test for convergence. Applications of the harmonic series and its partial sums include Euler's proof that there are infinitely many prime numbers, the analysis of the coupon collector's problem on how many random trials are needed to provide a complete range of responses, the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures (such as in combinatorics) through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance. For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 17th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action. Definition Let ''l'', ''m'', ''n'' be integers greater than or equal to 2. A triangle group Δ(''l'',''m'',''n'') is a group of motions of the Euclidean plane, the two-dimensional sphere, the real projective plane, or the hyperbolic plane generated by the reflections in the sides of a triangle with angles π/''l'', π/''m'' and π/''n'' (measured in radians). The product of the reflections in two adjacent sides is a rotation by the angle which is twice the angle between those sides, 2π/''l'', 2π/''m'' and 2π/''n''. Therefore, if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
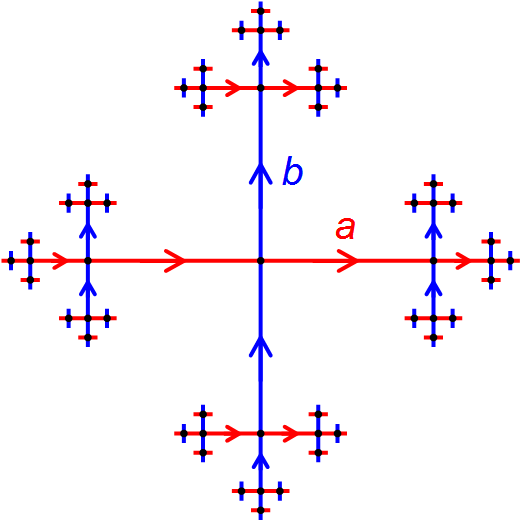
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such group (mathematics), groups and topology, topological and geometry, geometric properties of spaces on which these groups Group action (mathematics), act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph (discrete mathematics), graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |