|
Uniform Antiprismatic Prism
In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a ''p''-gonal antiprismatic prism is ''p'',2+,2 order 8''p''. A p-gonal antiprismatic prism or p-gonal antiduoprism has 2 ''p''-gonal antiprism, 2 ''p''-gonal prism, and ''2p'' triangular prism cells. It has 4''p'' equilateral triangle, 4''p'' square and 4 regular ''p''-gon faces. It has 10''p'' edges, and 4''p'' vertices. Convex uniform antiprismatic prisms There is an infinite series of convex uniform antiprismatic prisms, starting with the ''digonal antiprismatic prism'' is a tetrahedral prism, with two of the tetrahedral cells degenerated into squares. The ''triangular antiprismatic prism'' is the first nondegenerate form, which is also an octahedral prism. The remainder are unique uniform 4-polytopes. Star antiprismatic prisms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatic Uniform 4-polytope
In four-dimensional geometry, a prismatic uniform 4-polytope is a uniform 4-polytope with a nonconnected Coxeter diagram symmetry group. These figures are analogous to the set of prisms and antiprism uniform polyhedra, but add a third category called duoprisms, constructed as a product of two regular polygons. The prismatic uniform 4-polytopes consist of two infinite families: * Polyhedral prisms: products of a line segment and a uniform polyhedron. This family is infinite because it includes prisms built on 3-dimensional prisms and antiprisms. * Duoprisms: product of two regular polygons. Convex polyhedral prisms The most obvious family of prismatic 4-polytopes is the ''polyhedral prisms,'' i.e. products of a polyhedron with a line segment. The cells of such a 4-polytope are two identical uniform polyhedra lying in parallel hyperplanes (the ''base'' cells) and a layer of prisms joining them (the ''lateral'' cells). This family includes prisms for the 75 nonprismatic uniform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle. Principal properties Denoting the common length of the sides of the equilateral triangle as a, we can determine using the Pythagorean theorem that: *The area is A=\frac a^2, *The perimeter is p=3a\,\! *The radius of the circumscribed circle is R = \frac *The radius of the inscribed circle is r=\frac a or r=\frac *The geometric center of the triangle is the center of the circumscribed and inscribed circles *The altitude (height) from any side is h=\frac a Denoting the radius of the circumscribed circle as ''R'', we can determine using trigonometry that: *The area of the triangle is \mathrm=\fracR^2 Many of these quantities have simple r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
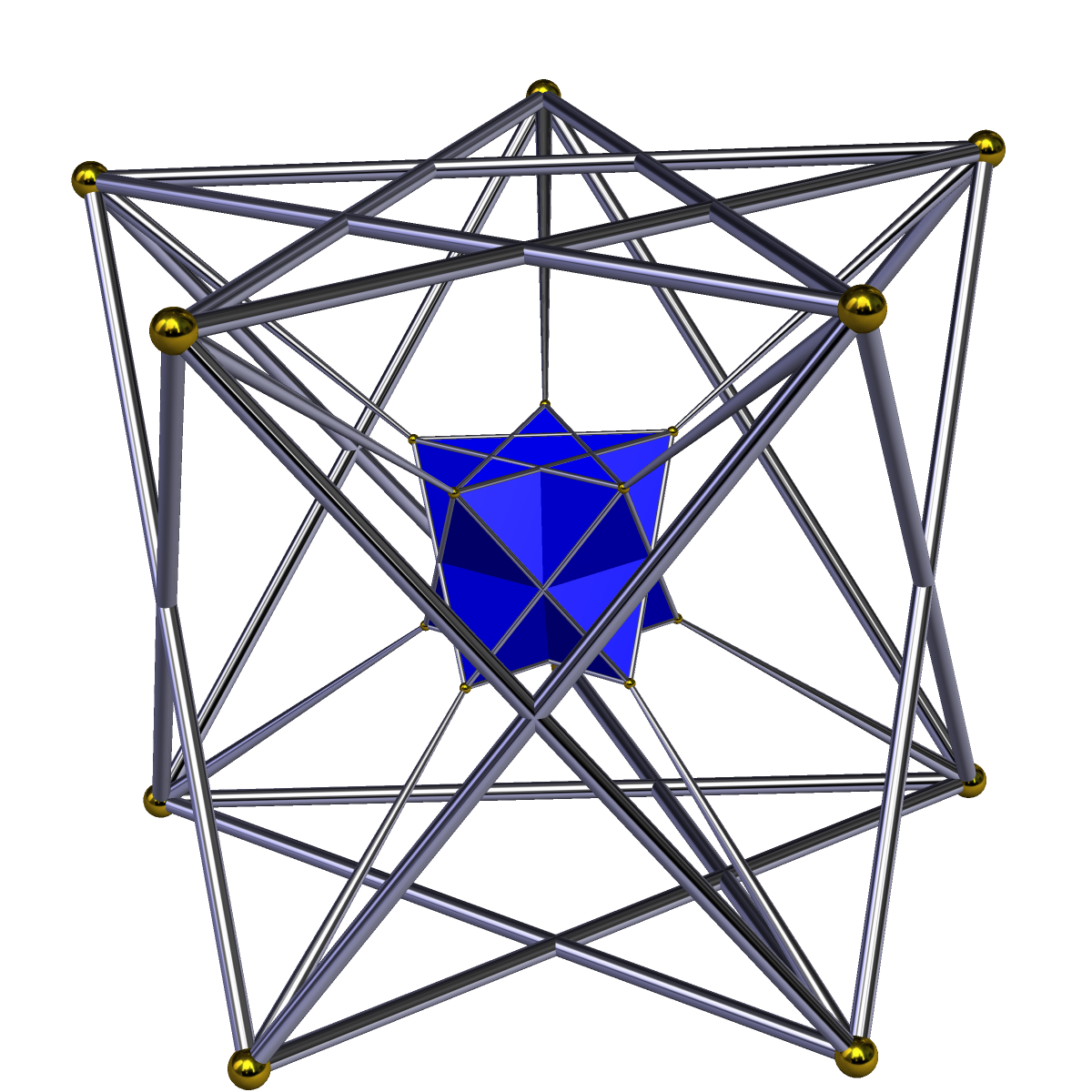
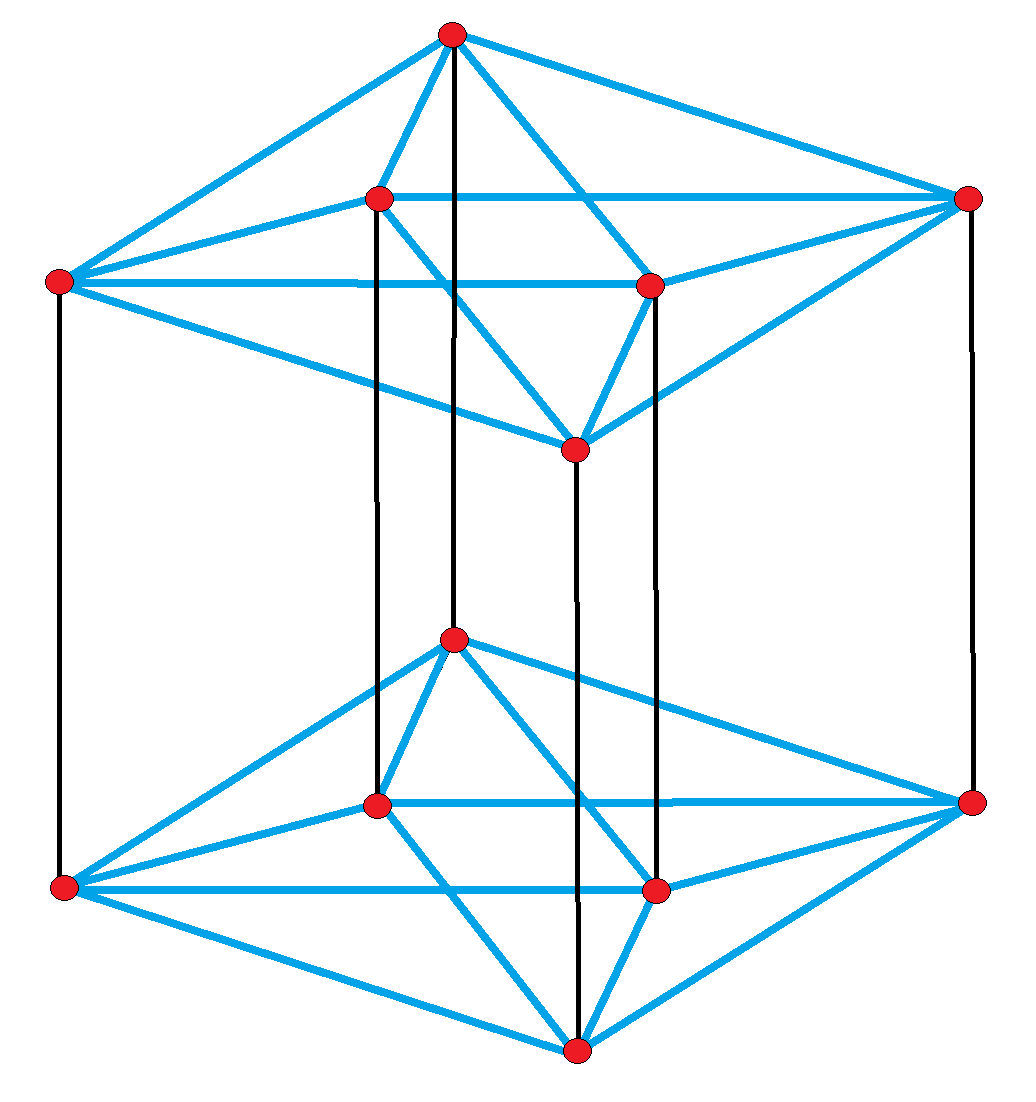
Crossed Pentagrammic Antiprismatic Prism
{{disambiguation ...
Crossed may refer to: * ''Crossed'' (comics), a 2008 comic book series by Garth Ennis * ''Crossed'' (novel), a 2010 young adult novel by Ally Condie * "Crossed" (''The Walking Dead''), an episode of the television series ''The Walking Dead'' See also *Cross (other) A cross is a geometrical figure consisting of two intersecting lines or bars. Cross or The Cross may also refer to: Religion * Christian cross, the basic symbol of Christianity * Cross necklace, a necklace worn by adherents of the Christian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Crossed Antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams. This polyhedron is identified with the indexed name U80 as a uniform polyhedron. The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron. See also * Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoid ... External links * *http://www.mathconsult.ch/sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Prism
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams. It is a special case of a right prism with a pentagram as base, which in general has rectangular non-base faces. Topologically it is the same as a convex pentagonal prism. It is the 78th model in the list of uniform polyhedra, as the first representative of uniform star prisms, along with the pentagrammic antiprism, which is the 79th model. Geometry It has 7 faces, 15 edges and 10 vertices. This polyhedron is identified with the indexed name U78 as a uniform polyhedron. The triangle face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered a angel or exterior depending on how the interior is defined. One definition of the interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the diameter Gallery Pentagr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Antiprism
In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It has 12 faces, 20 edges and 10 vertices. This polyhedron is identified with the indexed name U79 as a uniform polyhedron. Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter. In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon. Gallery Net Net (fold the dotted line in the centre in the opposite direction to all the other lines): : See also * Prismatic uniform polyhedron *Pentagrammic prism *Pentagrammic crossed-antiprism In geometry, the pentagrammic crossed-antipris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prismatic Uniform Polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismatoids. Vertex configuration and symmetry groups Because they are isogonal (vertex-transitive), their vertex arrangement uniquely corresponds to a symmetry group. The difference between the prismatic and antiprismatic symmetry groups is that D''p''h has the vertices lined up in both planes, which gives it a reflection plane perpendicular to its ''p''-fold axis (parallel to the polygon); while D''p''d has the vertices twisted relative to the other plane, which gives it a rotatory reflection. Each has ''p'' reflection planes which contain the ''p''-fold axis. The D''p''h symmetry group contains inversion if and only if ''p'' is even, while D''p''d contains inversion symmetry if and only if ''p'' is odd. Enumeration There are: * p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedral Prism
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms. Alternative names *Octahedral dyadic prism ( Norman W. Johnson) *Ope (Jonathan Bowers, for octahedral prism) *Triangular antiprismatic prism *Triangular antiprismatic hyperprism Coordinates It is a Hanner polytope with vertex coordinates, permuting first 3 coordinates: :( ±1,0,0 ±1) Structure The octahedral prism consists of two octahedra connected to each other via 8 triangular prisms. The triangular prisms are joined to each other via their square faces. Projections The octahedron-first orthographic projection of the octahedral prism into 3D space has an octahedral envelope. The two octahedral cells project onto the entire volume of this envelope, while the 8 triangular prismic cells project onto its 8 triangular faces. The triangular-prism-first orthographic projection of the octahedral prism into 3D space has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Prism
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices. It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids. Images Alternative names # Tetrahedral dyadic prism ( Norman W. Johnson) # Tepe (Jonathan Bowers: for tetrahedral prism) # Tetrahedral hyperprism # Digonal antiprismatic prism # Digonal antiprismatic hyperprism Structure The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces. Projections The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
