 |
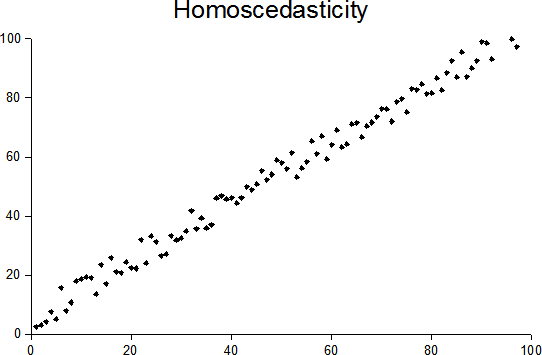
Unequal Variance
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
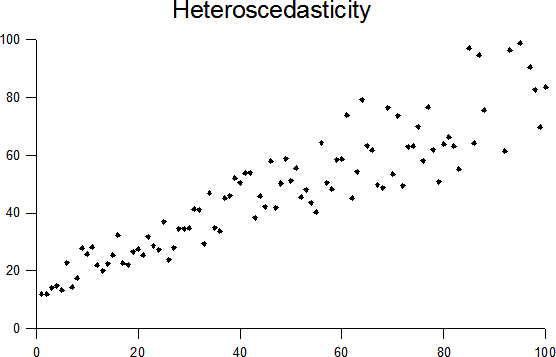 |
Homoscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Statistical Model Specification
In statistics, model specification is part of the process of building a statistical model: specification consists of selecting an appropriate functional form for the model and choosing which variables to include. For example, given personal income y together with years of schooling s and on-the-job experience x, we might specify a functional relationship y = f(s,x) as follows: : \ln y = \ln y_0 + \rho s + \beta_1 x + \beta_2 x^2 + \varepsilon where \varepsilon is the unexplained error term that is supposed to comprise independent and identically distributed Gaussian variables. The statistician Sir David Cox has said, "How hetranslation from subject-matter problem to statistical model is done is often the most critical part of an analysis". Specification error and bias Specification error occurs when the functional form or the choice of independent variables poorly represent relevant aspects of the true data-generating process. In particular, bias (the expected value of the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Asymptotic Distribution
In mathematics and statistics, an asymptotic distribution is a probability distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators. Definition A sequence of distributions corresponds to a sequence of random variables ''Zi'' for ''i'' = 1, 2, ..., I . In the simplest case, an asymptotic distribution exists if the probability distribution of ''Zi'' converges to a probability distribution (the asymptotic distribution) as ''i'' increases: see convergence in distribution. A special case of an asymptotic distribution is when the sequence of random variables is always zero or ''Zi'' = 0 as ''i'' approaches infinity. Here the asymptotic distribution is a degenerate distribution, corresponding to the value zero. However, the most usual sense in which the term asymptotic distribution is used ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Type I And Type II Errors
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a "false negative" finding or conclusion; example: "a guilty person is not convicted"). Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process. By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased. The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science. Intuitively, type I errors can be thought of as errors of ''commission'', i.e. the researcher unlu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
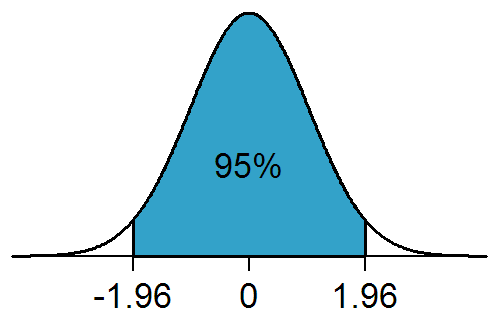 |
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Best Linear Unbiased Estimator
Best or The Best may refer to: People * Best (surname), people with the surname Best * Best (footballer, born 1968), retired Portuguese footballer Companies and organizations * Best & Co., an 1879–1971 clothing chain * Best Lock Corporation, a lock manufacturer * Best Manufacturing Company, a farm machinery company * Best Products, a chain of catalog showroom retail stores * Brihanmumbai Electric Supply and Transport, a public transport and utility provider * Best High School (other) Acronyms * Berkeley Earth Surface Temperature, a project to assess global temperature records * BEST Robotics, a student competition * BioEthanol for Sustainable Transport * Bootstrap error-adjusted single-sample technique, a statistical method * Bringing Examination and Search Together, a European Patent Office initiative * Bronx Environmental Stewardship Training, a program of the Sustainable South Bronx organization * Smart BEST, a Japanese experimental train * Brihanmumbai Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gauss–Markov Theorem
In statistics, the Gauss–Markov theorem (or simply Gauss theorem for some authors) states that the ordinary least squares (OLS) estimator has the lowest sampling variance within the class of linear unbiased estimators, if the errors in the linear regression model are uncorrelated, have equal variances and expectation value of zero. The errors do not need to be normal, nor do they need to be independent and identically distributed (only uncorrelated with mean zero and homoscedastic with finite variance). The requirement that the estimator be unbiased cannot be dropped, since biased estimators exist with lower variance. See, for example, the James–Stein estimator (which also drops linearity), ridge regression, or simply any degenerate estimator. The theorem was named after Carl Friedrich Gauss and Andrey Markov, although Gauss' work significantly predates Markov's. But while Gauss derived the result under the assumption of independence and normality, Markov reduced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Scedastic Function
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y, X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\mid X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y, X) itself is a random variable (and is a function of ''X''). Explanation, rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Simple Linear Regression
In statistics, simple linear regression is a linear regression model with a single explanatory variable. That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the ''x'' and ''y'' coordinates in a Cartesian coordinate system) and finds a linear function (a non-vertical straight line) that, as accurately as possible, predicts the dependent variable values as a function of the independent variable. The adjective ''simple'' refers to the fact that the outcome variable is related to a single predictor. It is common to make the additional stipulation that the ordinary least squares (OLS) method should be used: the accuracy of each predicted value is measured by its squared '' residual'' (vertical distance between the point of the data set and the fitted line), and the goal is to make the sum of these squared deviations as small as possible. Other regression methods that can be used in place of ordinary least sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Autoregressive Conditional Heteroscedasticity
In econometrics, the autoregressive conditional heteroskedasticity (ARCH) model is a statistical model for time series data that describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms; often the variance is related to the squares of the previous innovations. The ARCH model is appropriate when the error variance in a time series follows an autoregressive (AR) model; if an autoregressive moving average (ARMA) model is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH) model. ARCH models are commonly employed in modeling financial time series that exhibit time-varying volatility and volatility clustering, i.e. periods of swings interspersed with periods of relative calm. ARCH-type models are sometimes considered to be in the family of stochastic volatility models, although this is strictly incorrect since at time ''t'' the volatility i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |