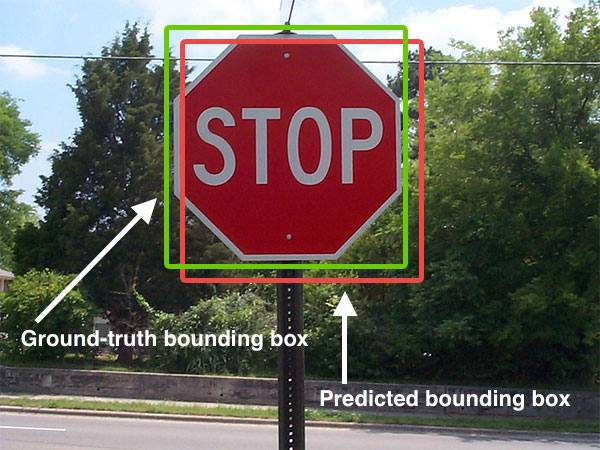
|
Triangulation (computer Vision)
In computer vision, triangulation refers to the process of determining a point in 3D space given its projections onto two, or more, images. In order to solve this problem it is necessary to know the parameters of the camera projection function from 3D to 2D for the cameras involved, in the simplest case represented by the camera matrices. Triangulation is sometimes also referred to as reconstruction or intersection. The triangulation problem is in principle trivial. Since each point in an image corresponds to a line in 3D space, all points on the line in 3D are projected to the point in the image. If a pair of corresponding points in two, or more images, can be found it must be the case that they are the projection of a common 3D point x. The set of lines generated by the image points must intersect at x (3D point) and the algebraic formulation of the coordinates of x (3D point) can be computed in a variety of ways, as is presented below. In practice, however, the coordin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Neighborhood Operation
In computer vision and image processing a neighborhood operation is a commonly used class of computations on image data which implies that it is processed according to the following pseudo code: Visit each point p in the image data and do This general procedure can be applied to image data of arbitrary dimensionality. Also, the image data on which the operation is applied does not have to be defined in terms of intensity or color, it can be any type of information which is organized as a function of spatial (and possibly temporal) variables in . The result of applying a neighborhood operation on an image is again something which can be interpreted as an image, it has the same dimension as the original data. The value at each image point, however, does not have to be directly related to intensity or color. Instead it is an element in the range of the function , which can be of arbitrary type. Normally the neighborhood is of fixed size and is a square (or a cube, depending ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Line–line Intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set, a point (geometry), point, or another Line (geometry), line. Distinguishing these cases and finding the Intersection (Euclidean geometry), intersection have uses, for example, in computer graphics, motion planning, and collision detection. In three-dimensional Euclidean geometry, if two lines are not in the same plane (geometry), plane, they have no point of intersection and are called skew lines. If they are in the same plane, however, there are three possibilities: if they coincide (are not distinct lines), they have an infinitude of points in common (namely all of the points on either of them); if they are distinct but have the same slope, they are said to be parallel (geometry), parallel and have no points in common; otherwise, they have a single point of intersection. The distinguishing features of non-Euclidean geometry are the number and locations of possible intersections between two lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bundle Adjustment
In photogrammetry and computer stereo vision, bundle adjustment is simultaneous refining of the 3D coordinates describing the scene geometry, the parameters of the relative motion, and the optical characteristics of the camera(s) employed to acquire the images, given a set of images depicting a number of 3D points from different viewpoints. Its name refers to the '' geometrical bundles'' of light rays originating from each 3D feature and converging on each camera's optical center, which are adjusted optimally according to an optimality criterion involving the corresponding image projections of all points. Uses Bundle adjustment is almost always used as the last step of feature-based 3D reconstruction algorithms. It amounts to an optimization problem on the 3D structure and viewing parameters (i.e., camera pose and possibly intrinsic calibration and radial distortion), to obtain a reconstruction which is optimal under certain assumptions regarding the noise pertaining to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
3D Reconstruction From Multiple Images
3D reconstruction from multiple images is the creation of three-dimensional models from a set of images. It is the reverse process of obtaining 2D images from 3D scenes. The essence of an image is to project a 3D scene onto a 2D plane, during which process, the depth is lost. The 3D point corresponding to a specific image point is constrained to be on the line of sight. From a single image, it is impossible to determine which point on this line corresponds to the image point. If two images are available, then the position of a 3D point can be found as the intersection of the two projection rays. This process is referred to as triangulation. The key for this process is the relations between multiple views, which convey that the corresponding sets of points must contain some structure, and that this structure is related to the poses and the calibration of the camera. In recent decades, there has been a significant demand for 3D content in application to computer graphics, vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Essential Matrix
In computer vision, the essential matrix is a 3 \times 3 matrix, \mathbf that relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera model. Function More specifically, if \mathbf and \mathbf' are homogeneous ''normalized'' image coordinates in image 1 and 2, respectively, then : (\mathbf')^\top \, \mathbf \, \mathbf = 0 if \mathbf and \mathbf' correspond to the same 3D point in the scene (not an "if and only if" due to the fact that points that lie on the same epipolar line in the first image will get mapped to the same epipolar line in the second image). The above relation which defines the essential matrix was published in 1981 by H. Christopher Longuet-Higgins, introducing the concept to the computer vision community. Richard Hartley and Andrew Zisserman's book reports that an analogous matrix appeared in photogrammetry long before that. Longuet-Higgins' paper includes an algorithm for estimating \mathbf from a se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a Matrix decomposition, factorization of a real number, real or complex number, complex matrix (mathematics), matrix into a rotation, followed by a rescaling followed by another rotation. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any matrix. It is related to the polar decomposition#Matrix polar decomposition, polar decomposition. Specifically, the singular value decomposition of an m \times n complex matrix is a factorization of the form \mathbf = \mathbf, where is an complex unitary matrix, \mathbf \Sigma is an m \times n rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \mathbf V^* is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrix, orthogonal matrices; in such contexts, the SVD ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fundamental Matrix (computer Vision)
In computer vision, the fundamental matrix \mathbf is a 3×3 matrix which relates corresponding points in stereo images. In epipolar geometry, with homogeneous image coordinates, x and x′, of corresponding points in a stereo image pair, Fx describes a line (an epipolar line) on which the corresponding point x′ on the other image must lie. That means, for all pairs of corresponding points holds : \mathbf'^ \mathbf = 0. Being of rank two and determined only up to scale, the fundamental matrix can be estimated given at least seven point correspondences. Its seven parameters represent the only geometric information about cameras that can be obtained through point correspondences alone. The term "fundamental matrix" was coined by QT Luong in his influential PhD thesis. It is sometimes also referred to as the "bifocal tensor". As a tensor it is a two-point tensor in that it is a bilinear form relating points in distinct coordinate systems. The above relation which defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Epipolar Constraint
Epipolar geometry is the geometry of stereo vision. When two cameras view a 3D scene from two distinct positions, there are a number of geometric relations between the 3D points and their projections onto the 2D images that lead to constraints between the image points. These relations are derived based on the assumption that the cameras can be approximated by the pinhole camera model. Definitions The figure below depicts two pinhole cameras looking at point X. In real cameras, the image plane is actually behind the focal center, and produces an image that is symmetric about the focal center of the lens. Here, however, the problem is simplified by placing a ''virtual image plane'' in front of the focal center i.e. optical center of each camera lens to produce an image not transformed by the symmetry. OL and OR represent the centers of symmetry of the two cameras lenses. X represents the point of interest in both cameras. Points xL and xR are the projections of point X onto t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Point Spread Function
The point spread function (PSF) describes the response of a focused optical imaging system to a point source or point object. A more general term for the PSF is the system's impulse response; the PSF is the impulse response or impulse response function (IRF) of a focused optical imaging system. The PSF in many contexts can be thought of as the shapeless blob in an image that should represent a single point object. We can consider this as a spatial impulse response function. In functional terms, it is the spatial domain version (i.e., the inverse Fourier transform) of the Optical transfer function, optical transfer function (OTF) of an imaging system. It is a useful concept in Fourier optics, astronomy, astronomical imaging, medical imaging, electron microscope, electron microscopy and other imaging techniques such as dimension, 3D microscopy (like in confocal laser scanning microscopy) and fluorescence microscopy. The degree of spreading (blurring) in the image of a point ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Camera Matrix
In computer vision Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical ... a camera matrix or (camera) projection matrix is a 3 \times 4 matrix (mathematics), matrix which describes the mapping of a pinhole camera from 3D points in the world to 2D points in an image. Let \mathbf be a representation of a 3D point in homogeneous coordinates (a 4-dimensional vector), and let \mathbf be a representation of the image of this point in the pinhole camera (a 3-dimensional vector). Then the following relation holds : \mathbf \sim \mathbf \, \mathbf where \mathbf is the camera matrix and the \, \sim sign implies that the left and right hand sides are equal Modulo (mathematics), except for a multiplication by a non-zero scalar k \neq 0: : \mathbf = k \, \mathbf \, \mathbf . Since th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Distortion (optics)
In geometric optics, distortion is a deviation from rectilinear projection; a projection in which straight lines in a scene remain straight in an image. It is a form of optical aberration that may be distinguished from other aberrations such as spherical aberration, coma, chromatic aberration, field curvature, and astigmatism in a sense that these impact the image sharpness without changing an object shape or structure in the image (e.g., a straight line in an object is still a straight line in the image although the image sharpness may be degraded by the mentioned aberrations) while distortion can change the object structure in the image (so named as distortion). Radial distortion Although distortion can be irregular or follow many patterns, the most commonly encountered distortions are radially symmetric, or approximately so, arising from the symmetry of a photographic lens. These ''radial distortions'' can usually be classified as either ''barrel'' distortions or ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |