|
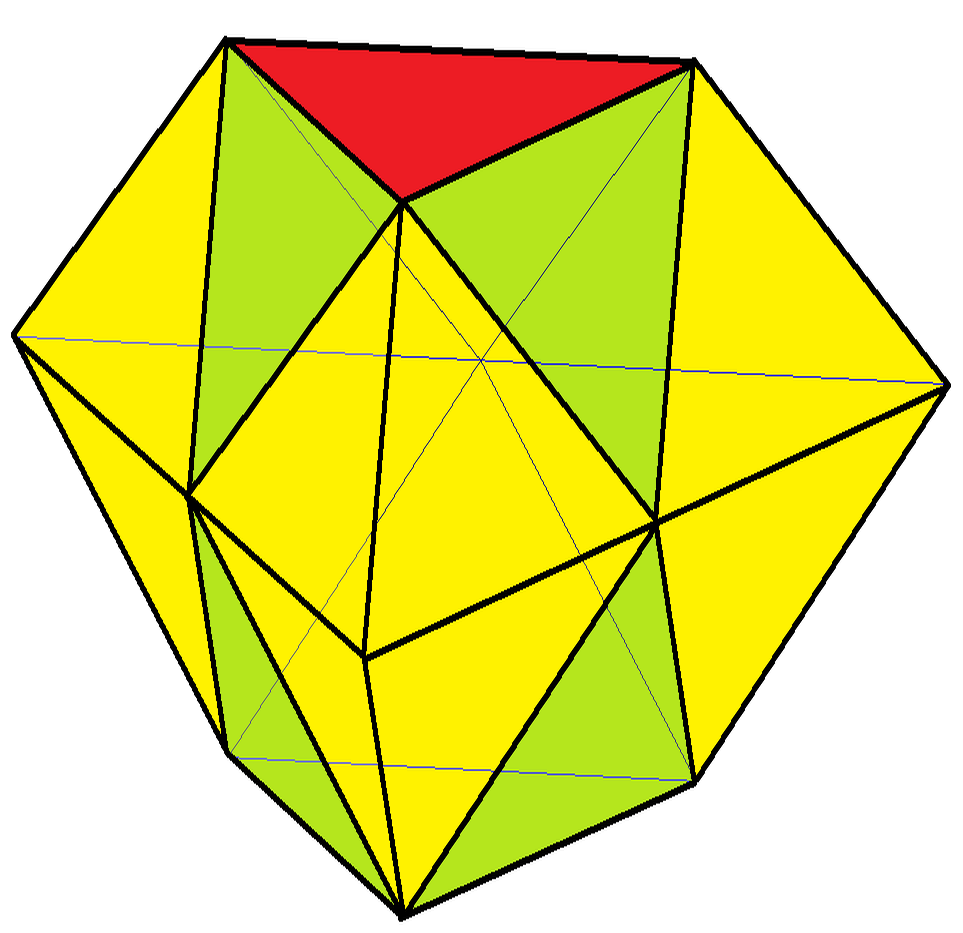
Triangular Bifrustum
In geometry, the triangular bifrustum is the second in an infinite series of bifrustum polyhedra. It has 6 trapezoid and 2 triangle faces. It may also be called the truncated triangular bipyramid; however, that term is ambiguous, as it may also refer to polyhedra formed by Truncation (geometry), truncating all five vertices of a triangular bipyramid. This polyhedron can be constructed by taking a triangular bipyramid and truncating the polar axis vertices, making it into two end-to-end frustums. It appears as the form of certain nanocrystals.. A truncated triangular bipyramid can be constructed by connecting two stacked regular octahedra with 3 pairs of tetrahedra around the sides. This represents a portion of the gyrated alternated cubic honeycomb. : References {{reflist External linksConway Notation for Polyhedra Try: t3dP3 Polyhedra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifrustum
In geometry, an -agonal bifrustum is a polyhedron composed of three parallel planes of -agons, with the middle plane largest and usually the top and bottom congruent. It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated. They are duals to the family of elongated bipyramids. Formulae For a regular -gonal bifrustum with the equatorial polygon sides , bases sides and semi-height (half the distance between the planes of bases) , the lateral surface area , total area and volume are: and \begin A_l &= n (a+b) \sqrt \\ pt A &= A_l + n \frac \\ pt V &= n \frach \end Note that the volume V is twice the volume of a frusta. Forms Three bifrusta are duals to three Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
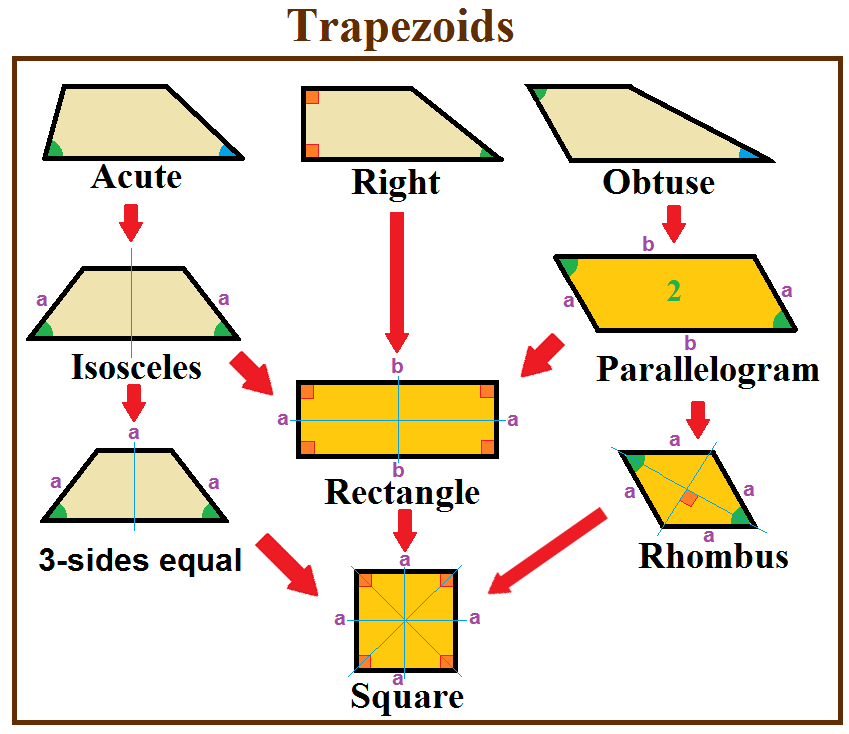
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Bipyramid
In geometry, the elongated triangular bipyramid (or dipyramid) or triakis triangular prism a polyhedron constructed from a triangular prism by attaching two tetrahedrons to its bases. It is an example of Johnson solid. Construction The elongated triangular bipyramid is constructed from a triangular prism by attaching two tetrahedrons onto its bases, a process known as the elongation. These tetrahedrons cover the triangular faces so that the resulting polyhedron has nine faces (six of them are equilateral triangles and three of them are squares), fifteen edges, and eight vertices. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated bipyramid is one of them, enumerated as the fourteenth Johnson solid J_ . Properties The surface area of an elongated triangular bipyramid A is the sum of all polygonal face's area: six equilateral triangles and three squares. The volume of an elongated triangular bipyramid V can be ascertaine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifrustum
In geometry, an -agonal bifrustum is a polyhedron composed of three parallel planes of -agons, with the middle plane largest and usually the top and bottom congruent. It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated. They are duals to the family of elongated bipyramids. Formulae For a regular -gonal bifrustum with the equatorial polygon sides , bases sides and semi-height (half the distance between the planes of bases) , the lateral surface area , total area and volume are: and \begin A_l &= n (a+b) \sqrt \\ pt A &= A_l + n \frac \\ pt V &= n \frach \end Note that the volume V is twice the volume of a frusta. Forms Three bifrusta are duals to three Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new Facet (geometry), facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Bipyramid
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid. Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century. Special cases As a right bipyramid Like other bipyramids, a triangular bipyramid can be constructed by attaching two tetrahedra face-to-face. These tetrahedra cover their triangular base, and the resulting polyhedron has six triangles, fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a ; (: frusta or frustums) is the portion of a polyhedron, solid (normally a pyramid (geometry), pyramid or a cone (geometry), cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A ''right frustum'' is a right pyramid or a right cone truncation (geometry), truncated perpendicularly to its axis; otherwise, it is an ''oblique frustum''. In a ''truncated cone'' or ''truncated pyramid'', the truncation plane is necessarily parallel to the cone's base, as in a frustum. If all its edges are forced to become of the same length, then a frustum becomes a ''Prism (geometry), prism'' (possibly oblique or/and with irregular bases). Elements, special cases, and related concepts A frustum's axis is that of the original cone or pyramid. A frustum is circular if it has circular bases; it is right if the axis is perpendicular to both bases, and oblique otherwise. The height of a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedra
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |