|
Terminal Yield
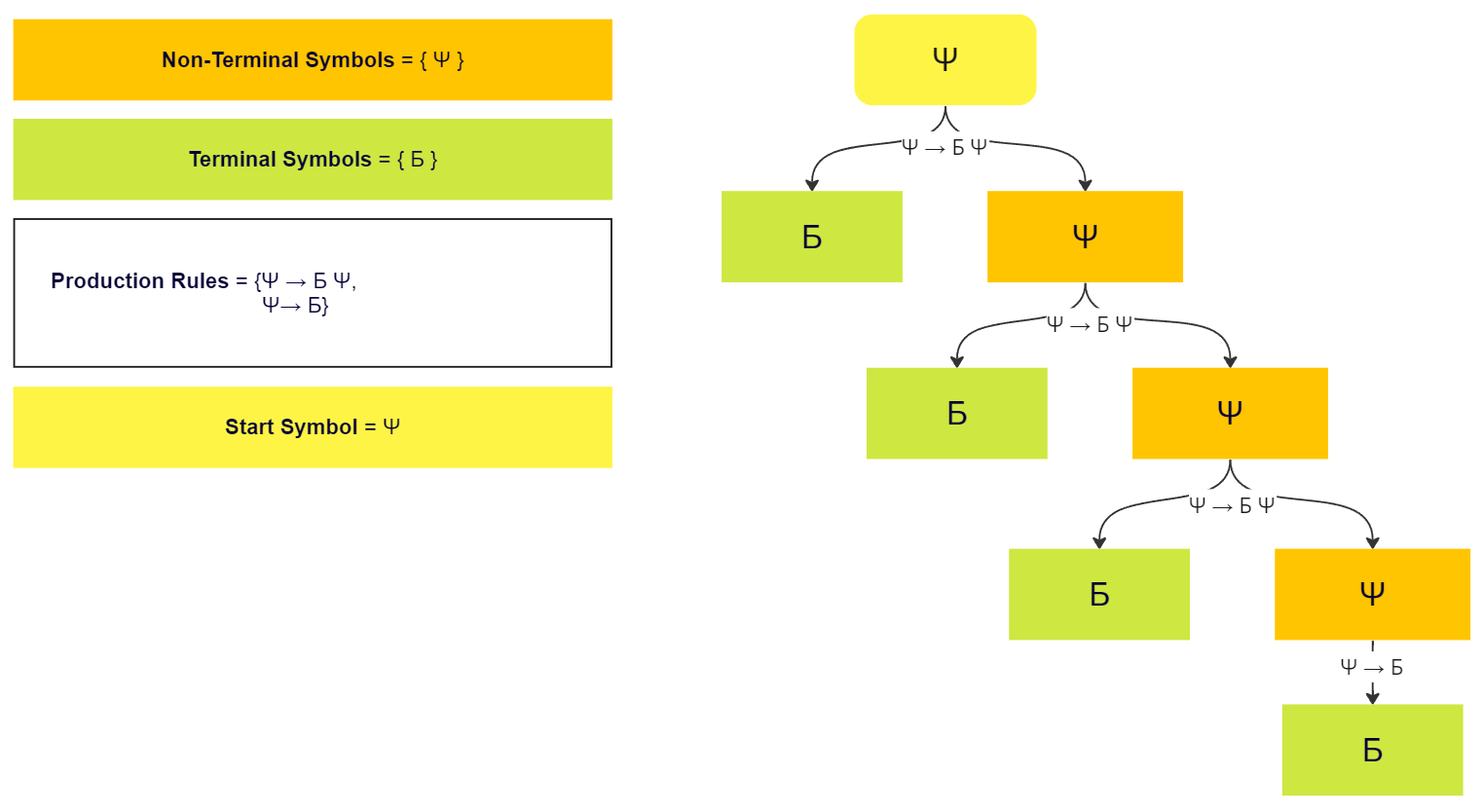
In formal language theory, the terminal yield (or fringe) of a tree is the sequence of leaves encountered in an ordered walk of the tree. Parse trees and/or derivation trees are encountered in the study of phrase structure grammars such as context-free grammars or linear grammars. The leaves of a derivation tree for a formal grammar ''G'' are the terminal symbols of that grammar, and the internal nodes the nonterminal or variable symbols. One can read off the corresponding terminal string by performing an ordered tree traversal In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a Tree (data structure), tree data stru ... and recording the terminal symbols in the order they are encountered. The resulting sequence of terminals is a string of the language ''L''(''G'') generated by the grammar ''G''. Formal languages ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Formal Language Theory
In logic, mathematics, computer science, and linguistics, a formal language is a set of string (computer science), strings whose symbols are taken from a set called "#Definition, alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called Formal language#Definition, ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tree Data Structure
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be connected to exactly one parent, except for the ''root'' node, which has no parent (i.e., the root node as the top-most node in the tree hierarchy). These constraints mean there are no cycles or "loops" (no node can be its own ancestor), and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes (parent and children nodes of a node under consideration, if they exist) in a single straight line (called edge or link between two adjacent nodes). Binary trees are a commonly used type, which constrain the number of children for each parent to at most two. When ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Phrase Structure Grammar
The term phrase structure grammar was originally introduced by Noam Chomsky as the term for grammar studied previously by Emil Post and Axel Thue ( Post canonical systems). Some authors, however, reserve the term for more restricted grammars in the Chomsky hierarchy: context-sensitive grammars or context-free grammars. In a broader sense, phrase structure grammars are also known as ''constituency grammars''. The defining character of phrase structure grammars is thus their adherence to the constituency relation, as opposed to the dependency relation of dependency grammars. History In 1956, Chomsky wrote, "A phrase-structure grammar is defined by a finite vocabulary (alphabet) Vp, and a finite set Σ of initial strings in Vp, and a finite set F of rules of the form: X → Y, where X and Y are strings in Vp." Constituency relation In linguistics, phrase structure grammars are all those grammars that are based on the constituency relation, as opposed to the dependency relation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Context-free Grammar
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form : A\ \to\ \alpha with A a ''single'' nonterminal symbol, and \alpha a string of terminals and/or nonterminals (\alpha can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by \alpha on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form \alpha A \beta \rightarrow \alpha \gamma \beta with A a nonterminal symbol and \alpha, \beta, and \gamma strings of terminal and/or nonterminal symbols. A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the first rule in the picture, : \lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Formal Grammar
A formal grammar is a set of Terminal and nonterminal symbols, symbols and the Production (computer science), production rules for rewriting some of them into every possible string of a formal language over an Alphabet (formal languages), alphabet. A grammar does not describe the semantics, meaning of the strings — only their form. In applied mathematics, formal language theory is the discipline that studies formal grammars and languages. Its applications are found in theoretical computer science, theoretical linguistics, Formal semantics (logic), formal semantics, mathematical logic, and other areas. A formal grammar is a Set_(mathematics), set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Terminal Symbol
In formal languages, terminal and nonterminal symbols are parts of the ''vocabulary'' under a formal grammar. ''Vocabulary'' is a finite, nonempty set of symbols. ''Terminal symbols'' are symbols that cannot be replaced by other symbols of the vocabulary. ''Nonterminal symbols'' are symbols that can be replaced by other symbols of the vocabulary by the production rules under the same formal grammar. A formal grammar defines a formal language over the vocabulary of the grammar. In the context of formal language, the term ''vocabulary'' is more commonly known as ''alphabet''. Nonterminal symbols are also called ''syntactic variables''. Terminal symbols Terminal symbols are those symbols that can appear in the formal language defined by a formal grammar. The process of applying the production rules successively to a start symbol might not terminate, but if it terminates when there is no more production rule can be applied, the output string will consist only of terminal symb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tree Traversal
In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a Tree (data structure), tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well. Types Unlike linked lists, one-dimensional arrays and other List of data structures#Linear data structures, linear data structures, which are canonically traversed in linear order, trees may be traversed in multiple ways. They may be traversed in Depth-first search, depth-first or Breadth-first search, breadth-first order. There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searche ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |