|
Term Algebra
In universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set ''X'' of variables is exactly the free magma generated by ''X''. Other synonyms for the notion include absolutely free algebra and anarchic algebra. From a category theory perspective, a term algebra is the initial object for the category of all ''X''-generated algebras of the same signature, and this object, unique up to isomorphism, is called an initial algebra; it generates by homomorphic projection all algebras in the category. A similar notion is that of a Herbrand universe in logic, usually used under this name in logic programming, which is (absolutely freely) defined starting from the set of constants and function symbols in a set of clauses. That is, the Herbrand universe consists of all ground terms: terms that have no variables in them. An atomic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Algebra
Universal algebra (sometimes called general algebra) is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular Group (mathematics), groups as the object of study, in universal algebra one takes the class of groups as an object of study. Basic idea In universal algebra, an algebra (or algebraic Structure (mathematical logic), structure) is a set (mathematics), set ''A'' together with a collection of operations on ''A''. An ''n''-arity, ary operation (mathematics), operation on ''A'' is a function (mathematics), function that takes ''n'' elements of ''A'' and returns a single element of ''A''. Thus, a 0-ary operation (or ''nullary operation'') can be represented simply as an element of ''A'', or a ''Constant (mathematics), constant'', often denoted by a letter like ''a''. A 1-ary operation (or ''unary operation'') is simply a function from ''A'' to ''A'', often denoted by a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
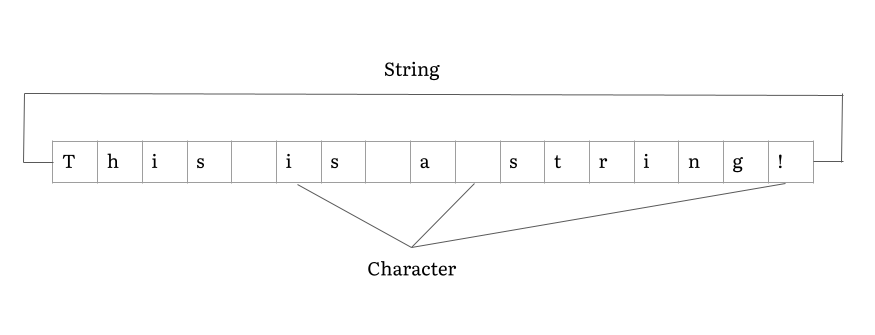
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term (logic)
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact. A first-order term is recursively constructed from constant symbols, variables and function symbols. An expression formed by applying a predicate symbol to an appropriate number of terms is called an atomic formula, which evaluates to true or false in bivalent logics, given an interpretation. For example, is a term built from the constant 1, the variable , and the binary function symbols and ; it is part of the atomic formula which evaluates to true for each real-numbered value of . Besides in logic, terms play important roles in universal algebra, and rewriting systems. Formal definition Given a set ''V'' of variable symbols, a set ''C'' of constant symbols and sets ''F''''n'' of ''n''-ary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arity
Arity () is the number of arguments or operands taken by a function, operation or relation in logic, mathematics, and computer science. In mathematics, arity may also be named ''rank'', but this word can have many other meanings in mathematics. In logic and philosophy, it is also called adicity and degree. In linguistics, it is usually named valency. Examples The term "arity" is rarely employed in everyday usage. For example, rather than saying "the arity of the addition operation is 2" or "addition is an operation of arity 2" one usually says "addition is a binary operation". In general, the naming of functions or operators with a given arity follows a convention similar to the one used for ''n''-based numeral systems such as binary and hexadecimal. One combines a Latin prefix with the -ary ending; for example: * A nullary function takes no arguments. ** Example: f()=2 * A unary function takes one argument. ** Example: f(x)=2x * A binary function takes two arguments. ** Examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Data Type
In computer science, an abstract data type (ADT) is a mathematical model for data types. An abstract data type is defined by its behavior (semantics) from the point of view of a '' user'', of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This mathematical model contrasts with data structures, which are concrete representations of data, and are the point of view of an implementer, not a user. Formally, an ADT may be defined as a "class of objects whose logical behavior is defined by a set of values and a set of operations"; this is analogous to an algebraic structure in mathematics. What is meant by "behaviour" varies by author, with the two main types of formal specifications for behavior being ''axiomatic (algebraic) specification'' and an ''abstract model;'' these correspond to axiomatic semantics and operational semantics of an abstract machine, respectively. Some authors also include the com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantics
Semantics (from grc, σημαντικός ''sēmantikós'', "significant") is the study of reference, meaning, or truth. The term can be used to refer to subfields of several distinct disciplines, including philosophy, linguistics and computer science. History In English, the study of meaning in language has been known by many names that involve the Ancient Greek word (''sema'', "sign, mark, token"). In 1690, a Greek rendering of the term ''semiotics'', the interpretation of signs and symbols, finds an early allusion in John Locke's ''An Essay Concerning Human Understanding'': The third Branch may be called [''simeiotikí'', "semiotics"], or the Doctrine of Signs, the most usual whereof being words, it is aptly enough termed also , Logick. In 1831, the term is suggested for the third branch of division of knowledge akin to Locke; the "signs of our knowledge". In 1857, the term '' semasiology'' (borrowed from German ''Semasiologie'') is attested in Josiah W. Gibbs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacques Herbrand
Jacques Herbrand (12 February 1908 – 27 July 1931) was a French mathematician. Although he died at age 23, he was already considered one of "the greatest mathematicians of the younger generation" by his professors Helmut Hasse and Richard Courant. He worked in mathematical logic and class field theory. He introduced recursive functions. '' Herbrand's theorem'' refers to either of two completely different theorems. One is a result from his doctoral thesis in proof theory, and the other one half of the Herbrand–Ribet theorem. The Herbrand quotient is a type of Euler characteristic, used in homological algebra. He contributed to Hilbert's program in the foundations of mathematics by providing a constructive consistency proof for a weak system of arithmetic. The proof uses the above-mentioned, proof-theoretic Herbrand's theorem. Biography Herbrand finished his doctorate at École Normale Supérieure in Paris under Ernest Vessiot in 1929. He joined the army in October 1929 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground Atom
In mathematical logic, a ground term of a formal system is a term that does not contain any variables. Similarly, a ground formula is a formula that does not contain any variables. In first-order logic with identity, the sentence Q(a) \lor P(b) is a ground formula, with a and b being constant symbols. A ground expression is a ground term or ground formula. Examples Consider the following expressions in first order logic over a signature containing the constant symbols 0 and 1 for the numbers 0 and 1, respectively, a unary function symbol s for the successor function and a binary function symbol + for addition. * s(0), s(s(0)), s(s(s(0))), \ldots are ground terms; * 0 + 1, \; 0 + 1 + 1, \ldots are ground terms; * 0+s(0), \; s(0)+ s(0), \; s(0)+s(s(0))+0 are ground terms; * x + s(1) and s(x) are terms, but not ground terms; * s(0) = 1 and 0 + 0 = 0 are ground formulae. Formal definitions What follows is a formal definition for first-order languages. Let a first-order language ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate (mathematical Logic)
In logic, a predicate is a symbol which represents a property or a relation. For instance, in the first order formula P(a), the symbol P is a predicate which applies to the individual constant a. Similarly, in the formula R(a,b), R is a predicate which applies to the individual constants a and b. In the semantics of logic, predicates are interpreted as relations. For instance, in a standard semantics for first-order logic, the formula R(a,b) would be true on an interpretation if the entities denoted by a and b stand in the relation denoted by R. Since predicates are non-logical symbols, they can denote different relations depending on the interpretation used to interpret them. While first-order logic only includes predicates which apply to individual constants, other logics may allow predicates which apply to other predicates. Predicates in different systems * In propositional logic, atomic formulas are sometimes regarded as zero-place predicates In a sense, these are null ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Formula
In mathematical logic, an atomic formula (also known as an atom or a prime formula) is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic. Compound formulas are formed by combining the atomic formulas using the logical connectives. The precise form of atomic formulas depends on the logic under consideration; for propositional logic, for example, a propositional variable is often more briefly referred to as an "atomic formula", but, more precisely, a propositional variable is not an atomic formula but a formal expression that denotes an atomic formula. For predicate logic, the atoms are predicate symbols together with their arguments, each argument being a term. In model theory, atomic formulas are merely strings of symbols with a given signature, which may or may not be satisfiable with respect to a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground Term
In mathematical logic, a ground term of a formal system is a term that does not contain any variables. Similarly, a ground formula is a formula that does not contain any variables. In first-order logic with identity, the sentence Q(a) \lor P(b) is a ground formula, with a and b being constant symbols. A ground expression is a ground term or ground formula. Examples Consider the following expressions in first order logic over a signature containing the constant symbols 0 and 1 for the numbers 0 and 1, respectively, a unary function symbol s for the successor function and a binary function symbol + for addition. * s(0), s(s(0)), s(s(s(0))), \ldots are ground terms; * 0 + 1, \; 0 + 1 + 1, \ldots are ground terms; * 0+s(0), \; s(0)+ s(0), \; s(0)+s(s(0))+0 are ground terms; * x + s(1) and s(x) are terms, but not ground terms; * s(0) = 1 and 0 + 0 = 0 are ground formulae. Formal definitions What follows is a formal definition for first-order languages. Let a first-order langua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |