|
Tangent Half-angle Substitution
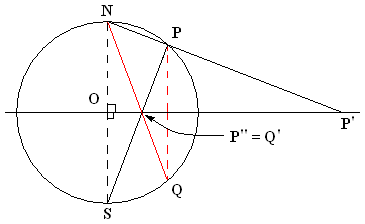
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfrac x2. This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is: \int f(\sin x, \cos x)\, dx =\int f \frac. The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to evaluate the integral \int dx / (a + b\cos x) in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name. It is known in Russia as the universal trigonometric substitution, and also known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Calculus
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an ''antiderivative'', a function whose der ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiation Rules
This article is a summary of differentiation rules, that is, rules for computing the derivative of a function (mathematics), function in calculus. Elementary rules of differentiation Unless otherwise stated, all functions are functions of real numbers (\mathbb) that return real values, although, more generally, the formulas below apply wherever they are well defined, including the case of complex numbers (\mathbb). Constant term rule For any value of c, where c \in \mathbb, if f(x) is the constant function given by f(x) = c, then \frac = 0. Proof Let c \in \mathbb and f(x) = c. By the definition of the derivative: \begin f'(x) &= \lim_\frac \\ &= \lim_ \frac \\ &= \lim_ \frac \\ &= \lim_ 0 \\ &= 0. \end This computation shows that the derivative of any constant function is 0. Intuitive (geometric) explanation The derivative of the function at a point is the slope of the line tangent to the curve at the point. The slope of the constant function is 0, because the Tangent, tangen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Stewart (mathematician)
James Drewry Stewart, (March 29, 1941December 3, 2014) was a Canadian mathematician, violinist, and professor emeritus of mathematics at McMaster University. Stewart is best known for his series of calculus textbooks used for high school, college, and university-level courses. Career Stewart received his master of science at Stanford University and his doctor of philosophy from the University of Toronto in 1967. He worked for two years as a postdoctoral fellow at the University of London, where his research focused on harmonic analysis, harmonic and functional analysis. His books are standard textbooks in universities in many countries. One of his best-known textbooks is ''Calculus: Early Transcendentals'' (1995), a set of textbooks which is accompanied by websitefor students. Stewart was also a violinist and a former member of the Hamilton Philharmonic Orchestra. Integral House From 2003 to 2009 a house designed by Brigitte Shim and Howard Sutcliffe was constructed for Ste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass (; ; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the " father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin. Among many other contributions, Weierstrass formalized the definition of the continuity of a function and complex analysis, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals. Biography Weierstrass was born into a Roman Catholic family in Ostenfelde, a village near Ennigerloh, in the Province of Westphalia. Karl Weierstrass was the son of Wilhelm Weierstrass and Theodora Vonderforst, the former of whom was a government official and both of whom were Cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Frederick Eberlein
William Frederick Eberlein (June 25, 1917, Shawano, Wisconsin – 1986, Rochester, New York) was an American mathematician, specializing in mathematical analysis and mathematical physics. Life Eberlein studied from 1936 to 1942 at the University of Wisconsin A university () is an institution of tertiary education and research which awards academic degrees in several academic disciplines. ''University'' is derived from the Latin phrase , which roughly means "community of teachers and scholars". Uni ... and at Harvard University, where he received in 1942 a PhD for the thesis ''Closure, Convexity, and Linearity in Banach Spaces'' under the direction of Marshall Harvey Stone, Marshall Stone. He was married twice—to Mary Bernarda Barry and Patricia Ramsay James. He had four children with Mary Barry, including Patrick Barry Eberlein, another renowned mathematician. Patricia Ramsay James was a mathematician who moved into computer science as the field opened up; their one child i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Substitution
Euler substitution is a method for evaluating integrals of the form \int R(x, \sqrt) \, dx, where R is a rational function of x and \sqrt. In such cases, the integrand can be changed to a rational function by using the substitutions of Euler. Euler's first substitution The first substitution of Euler is used when a > 0. We substitute \sqrt = \pm x\sqrt + t and solve the resulting expression for x. We have that x = \frac and that the dx term is expressible rationally in t. In this substitution, either the positive sign or the negative sign can be chosen. Euler's second substitution If c > 0, we take \sqrt = xt \pm \sqrt. We solve for x similarly as above and find x = \frac. Again, either the positive or the negative sign can be chosen. Euler's third substitution If the polynomial ax^2 + bx + c has real roots \alpha and \beta, we may choose \sqrt = \sqrt = (x - \alpha)t. This yields x = \frac, and as in the preceding cases, we can express the entire integrand rationally i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Substitution
In mathematics, a trigonometric substitution replaces a trigonometric function for another expression. In calculus, trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration. Case I: Integrands containing ''a''2 − ''x''2 Let x = a \sin \theta, and use the identity 1-\sin^2 \theta = \cos^2 \theta. Examples of Case I Example 1 In the integral \int\frac, we may use x=a\sin \theta,\quad dx=a\cos\theta\, d\theta, \quad \theta=\arcsin\frac. Then, \begin \int\frac &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \int d\theta \\ pt &= \theta + C \\ pt &= \arcsin\frac+C. \end The above step requires that a > ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereographic Projection
In mathematics, a stereographic projection is a perspective transform, perspective projection of the sphere, through a specific point (geometry), point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth function, smooth, bijection, bijective function (mathematics), function from the entire sphere except the center of projection to the entire plane. It maps circle of a sphere, circles on the sphere to generalised circle, circles or lines on the plane, and is conformal map, conformal, meaning that it preserves angles at which curves meet and thus Local property, locally approximately preserves similarity (geometry), shapes. It is neither isometry, isometric (distance preserving) nor Equiareal map, equiareal (area preserving). The stereographic projection gives a way to representation (mathematics), represent a sphere by a plane. The metric tensor, metric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. If the defining polynomial of a plane algebraic curve is irreducible, then one has an ''irreducible plane algebraic curve''. Otherwise, the algebraic curve is the union of one or several irreducible curves, called its ''components'', that are defined by the irreducible factors. More generally, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Disk Model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle. The group of orientation preserving isometries of the disk model is given by the projective special unitary group , the quotient of the special unitary group SU(1,1) by its center . Along with the Klein model and the Poincaré half-space model, it was proposed by Eugenio Beltrami who used these models to show that hyperbolic geometry was equiconsistent with Euclidean geometry. It is named after Henri Poincaré, because his rediscovery of this representation fourteen years later became better known than the original work of Beltrami. The Poincaré ball model is the similar model for ''3'' or ''n''-dimensional hyperbolic geometry in which the points of the geometry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension ''n'' is the unique simply connected, ''n''-dimensional Riemannian manifold of constant sectional curvature equal to −1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to distinguish it from complex hyperbolic spaces. Hyperbolic space serves as the prototype of a Gromov hyperbolic space, which is a far-reaching notion including differential-geometric as well as more combinatorial spaces via a synthetic approach to negati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |