|
Standard Normal Deviate
A standard normal deviate is a normally distributed deviate. It is a realization of a standard normal random variable, defined as a random variable with expected value 0 and variance 1.Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms. OUP. Where collections of such random variables are used, there is often an associated (possibly unstated) assumption that members of such collections are statistically independent. Standard normal variables play a major role in theoretical statistics in the description of many types of models, particularly in regression analysis, the analysis of variance and time series analysis. When the term "deviate" is used, rather than "variable", there is a connotation that the value concerned is treated as the no-longer-random outcome of a standard normal random variable. The terminology here is the same as that for random variable and random variate. Standard normal deviates arise in practical statistics in two ways. :*Given a mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series Analysis
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''fore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the chi-squared distribution (also chi-square or \chi^2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution. The chi-squared distribution is used in the common chi-squared tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables. This contrasts with a conditional distribution, which gives the probabilities contingent upon the values of the other variables. Marginal variables are those variables in the subset of variables being retained. These concepts are "marginal" because they can be found by summing values in a table along rows or columns, and writing the sum in the margins of the table. The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing (that is, focusing on the sums in the margin) over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out. The context here is that the theoretic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudorandom Number Sequence
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's ''seed'' (which may include truly random values). Although sequences that are closer to truly random can be generated using hardware random number generators, ''pseudorandom number generators'' are important in practice for their speed in number generation and their reproducibility. PRNGs are central in applications such as simulations (e.g. for the Monte Carlo method), electronic games (e.g. for procedural generation), and cryptography. Cryptographic applications require the output not to be predictable from earlier outputs, and more elaborate algorithms, which do not inherit the linearity of simpler PRNGs, are needed. Good statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significance Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset (Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variate
In probability and statistics, a random variate or simply variate is a particular outcome of a ''random variable'': the random variates which are other outcomes of the same random variable might have different values ( random numbers). A random deviate or simply deviate is the difference of random variate with respect to the distribution central location (e.g., mean), often divided by the standard deviation of the distribution (i.e., as a standard score). Random variates are used when simulating processes driven by random influences ( stochastic processes). In modern applications, such simulations would derive random variates corresponding to any given probability distribution from computer procedures designed to create random variates corresponding to a uniform distribution, where these procedures would actually provide values chosen from a uniform distribution of pseudorandom numbers. Procedures to generate random variates corresponding to a given distribution are known as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deviate (statistics)
In probability and statistics, a random variate or simply variate is a particular outcome of a ''random variable'': the random variates which are other outcomes of the same random variable might have different values (random numbers). A random deviate or simply deviate is the difference of random variate with respect to the distribution central location (e.g., mean), often divided by the standard deviation of the distribution (i.e., as a standard score). Random variates are used when simulating processes driven by random influences (stochastic processes). In modern applications, such simulations would derive random variates corresponding to any given probability distribution from computer procedures designed to create random variates corresponding to a uniform distribution, where these procedures would actually provide values chosen from a uniform distribution of pseudorandom numbers. Procedures to generate random variates corresponding to a given distribution are known as pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
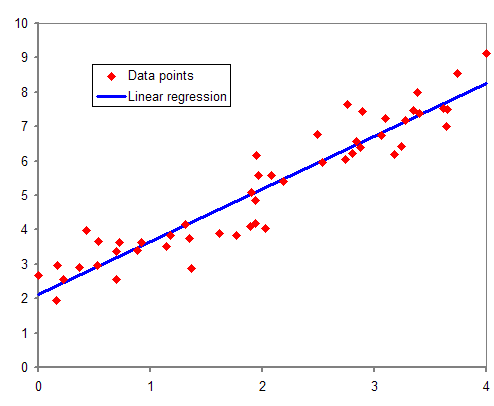
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistically Independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |