|
Spherical Conic
In mathematics, a spherical conic or sphero-conic is a curve on the sphere, the intersection of the sphere with a concentric elliptic cone. It is the spherical analog of a conic section ( ellipse, parabola, or hyperbola) in the plane, and as in the planar case, a spherical conic can be defined as the locus of points the sum or difference of whose great-circle distances to two foci is constant. By taking the antipodal point to one focus, every spherical ellipse is also a spherical hyperbola, and vice versa. As a space curve, a spherical conic is a quartic, though its orthogonal projections in three principal axes are planar conics. Like planar conics, spherical conics also satisfy a “reflection property”: the great-circle arcs from the two foci to any point on the conic have the tangent and normal to the conic at that point as their angle bisectors. Many theorems about conics in the plane extend to spherical conics. For example, Graves’s theorem and Ivory’s theorem ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric equation is: : (x,y) = (a\cos(t),b\sin(t)) \quad \text \quad 0\leq t\leq 2\pi. Ellip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Solid Geometry
Euclidean (or, less commonly, Euclidian) is an adjective derived from the name of Euclid, an ancient Greek mathematician. It is the name of: Geometry *Euclidean space, the two-dimensional plane and three-dimensional space of Euclidean geometry as well as their higher dimensional generalizations *Euclidean geometry, the study of the properties of Euclidean spaces *Non-Euclidean geometry, systems of points, lines, and planes analogous to Euclidean geometry but without uniquely determined parallel lines *Euclidean distance, the distance between pairs of points in Euclidean spaces * Euclidean ball, the set of points within some fixed distance from a center point Number theory *Euclidean division, the division which produces a quotient and a remainder *Euclidean algorithm, a method for finding greatest common divisors *Extended Euclidean algorithm, a method for solving the Diophantine equation ''ax'' + ''by'' = ''d'' where ''d'' is the greatest common divisor of ''a'' and ''b'' *Eu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion methods, and the use of numerical methods. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Curves
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TU Wien
TU Wien (TUW; german: Technische Universität Wien; still known in English as the Vienna University of Technology from 1975–2014) is one of the major universities in Vienna, Austria. The university finds high international and domestic recognition in teaching as well as in research, and it is a highly esteemed partner of innovation-oriented enterprises. It currently has about 28,100 students (29% women), eight faculties and about 5,000 staff members (3,800 academics). The university's teaching and research is focused on engineering, computer science, and natural sciences. History The institution was founded in 1815 by Emperor Francis I of Austria as the '' k.k. Polytechnische Institut'' (Imperial-Royal Polytechnic Institute). The first rector was Johann Joseph von Prechtl. It was renamed the ''Technische Hochschule'' (College of Technology) in 1872. When it began granting doctoral and higher degrees in 1975, it was renamed the ''Technische Universität Wien'' (Vienna Unive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Navigation
Hyperbolic navigation is a class of radio navigation systems in which a navigation receiver instrument is used to determine location based on the difference in timing ( phase) of radio waves received from radio navigation beacon transmitters. Such systems rely on the ability of two widely separated stations to broadcast a signal that is highly correlated in time. Typical systems either broadcast short pulses at the same time, or continual signals that are identical in phase. A receiver located at the midpoint between the two stations will receive the signals at the same time or have identical phase, but at any other location the signal from the closer station will be received first or have a different phase. Determining the location of a receiver requires that the two synchronized stations be tuned in at the same time so the signals can be compared. This reveals a ''difference'' in time, corresponding to a relative distance closer to one station or the other. Plotting all the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
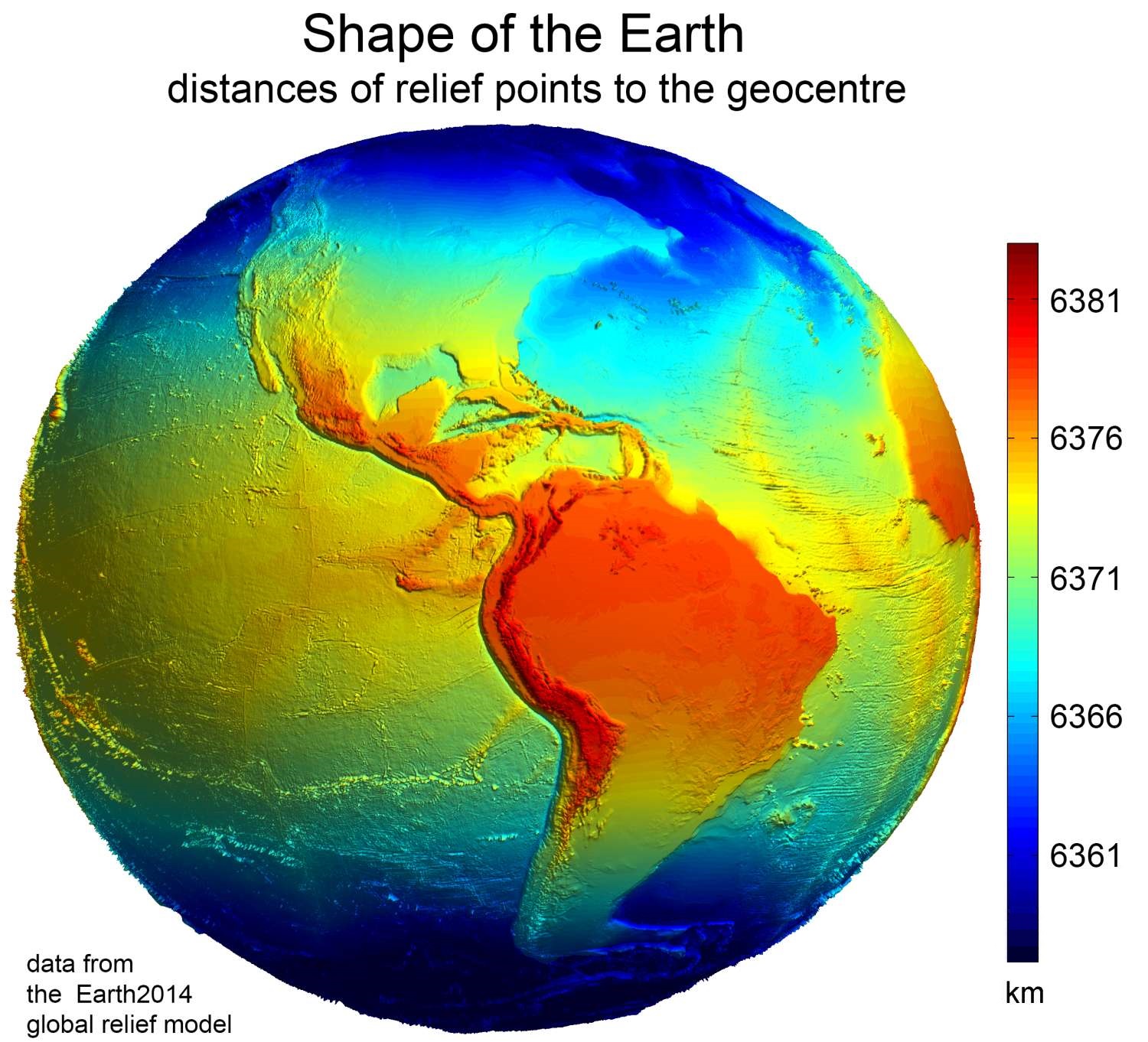
Osculating Sphere
Figure of the Earth is a term of art in geodesy that refers to the size and shape used to model Earth. The size and shape it refers to depend on context, including the precision needed for the model. A sphere is a well-known historical approximation of the figure of the Earth that is satisfactory for many purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of a spherical Earth offers a simple surface that is easy to deal with mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
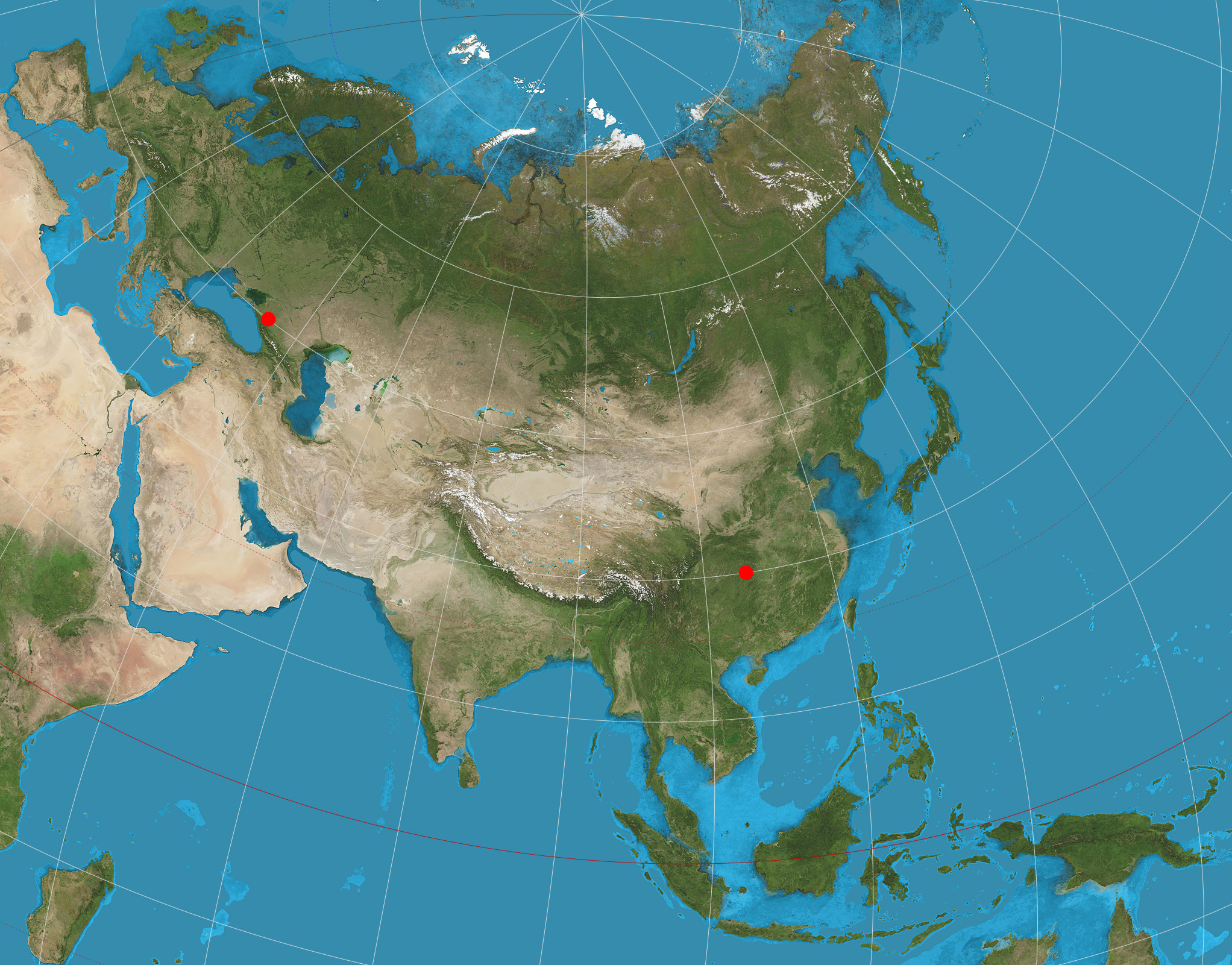
Two-point Equidistant Projection
The two-point equidistant projection or doubly equidistant projection is a map projection first described by Hans Maurer in 1919 and Charles Close in 1921. It is a generalization of the much simpler azimuthal equidistant projection. In this two-point form, two locus points are chosen by the mapmaker to configure the projection. Distances from the two loci to any other point on the map are correct: that is, they scale to the distances of the same points on the sphere. The two-point equidistant projection maps a family of confocal spherical conics onto two families of planar ellipses and hyperbolas. The projection has been used for all maps of the Asian continent by the National Geographic Society atlases since 1959, though its purpose in that case was to reduce distortion throughout Asia rather than to measure from the two loci. The projection sometimes appears in maps of air routes. The Chamberlin trimetric projection is a logical extension of the two-point idea to three poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force ''F'' that varies in strength as the inverse square of the distance ''r'' between them. The force may be either attractive or repulsive. The problem is to find the position or speed of the two bodies over time given their masses, positions, and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements. The Kepler problem is named after Johannes Kepler, who proposed Kepler's laws of planetary motion (which are part of classical mechanics and solved the problem for the orbits of the planets) and investigated the types of forces that would result in orbits obeying those laws (called ''Kepler's inverse problem''). For a discussion of the Kepler problem specific to radial orbits, see Radial trajectory. General relativity provides more accurate solutions to the two-body problem, especiall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Coordinate System
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci F_ and F_ are generally taken to be fixed at -a and +a, respectively, on the x-axis of the Cartesian coordinate system. Basic definition The most common definition of elliptic coordinates (\mu, \nu) is : x = a \ \cosh \mu \ \cos \nu : y = a \ \sinh \mu \ \sin \nu where \mu is a nonnegative real number and \nu \in , 2\pi On the complex plane, an equivalent relationship is : x + iy = a \ \cosh(\mu + i\nu) These definitions correspond to ellipses and hyperbolae. The trigonometric identity : \frac + \frac = \cos^ \nu + \sin^ \nu = 1 shows that curves of constant \mu form ellipses, whereas the hyperbolic trigonometric identity : \frac - \frac = \cosh^ \mu - \sinh^ \mu = 1 shows that curves of constant \nu form hyperbolae. Scale factors In an orthogonal coordinate system the lengths of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |