|
Skinny Triangle
In trigonometry, a skinny triangle is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to that angle in radians. The solution is particularly simple for skinny triangles that are also isosceles or right triangles: in these cases the need for trigonometric functions or tables can be entirely dispensed with. The skinny triangle finds uses in surveying, astronomy, and shooting. Isosceles triangle The approximated solution to the skinny isosceles triangle, referring to figure 1, is: :b \approx r \theta \, :\text \approx \frac \theta r^2 \, This is based on the small-angle approximations: :\sin\theta \approx \theta, \quad \theta \ll 1 \, and :\cos\theta = \sin\left(\frac-\theta \right) \approx 1, \quad \theta \ll 1 when \scriptstyle \theta is in radians. The proof of the skinny triangle solution follows from the small-angle approximation by apply ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Skinny Triangle
In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The two equal sides are called the legs and the third side is called the base of the triangle. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Skinny Triangle
Rights are legal, social, or ethical principles of freedom or entitlement; that is, rights are the fundamental normative rules about what is allowed of people or owed to people according to some legal system, social convention, or ethical theory. Rights are of essential importance in such disciplines as law and ethics, especially theories of justice and deontology. Rights are fundamental to any civilization and the history of social conflicts is often bound up with attempts both to define and to redefine them. According to the ''Stanford Encyclopedia of Philosophy'', "rights structure the form of governments, the content of laws, and the shape of morality as it is currently perceived". Definitional issues One way to get an idea of the multiple understandings and senses of the term is to consider different ways it is used. Many diverse things are claimed as rights: There are likewise diverse possible ways to categorize rights, such as: There has been considerable debate abou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minute Of Arc
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth circumference is very near . A minute of arc is of a radian. A second of arc, arcsecond (arcsec), or arc second, denoted by the symbol , is of an arcminute, of a degree, of a turn, and (about ) of a radian. These units originated in Babylonian astronomy as sexagesimal subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship. To express even smaller angles, standard SI prefixes can be employed; the milliarcsecond (mas) and microarcsecond (μas), for instance, are commonly used in ast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Mil
A milliradian ( SI-symbol mrad, sometimes also abbreviated mil) is an SI derived unit for angular measurement which is defined as a thousandth of a radian (0.001 radian). Milliradians are used in adjustment of firearm sights by adjusting the angle of the sight compared to the barrel (up, down, left, or right). Milliradians are also used for comparing shot groupings, or to compare the difficulty of hitting different sized shooting targets at different distances. When using a scope with both mrad adjustment and a reticle with mrad markings (called an "mrad/mrad scope"), the shooter can use the reticle as a ruler to count the number of mrads a shot was off-target, which directly translates to the sight adjustment needed to hit the target with a follow up shot. Optics with mrad markings in the reticle can also be used to make a range estimation of a known size target, or vice versa, to determine a target size if the distance is known, a practice called "milling". Milliradian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milliradian
A milliradian ( SI-symbol mrad, sometimes also abbreviated mil) is an SI derived unit for angular measurement which is defined as a thousandth of a radian (0.001 radian). Milliradians are used in adjustment of firearm sights by adjusting the angle of the sight compared to the barrel (up, down, left, or right). Milliradians are also used for comparing shot groupings, or to compare the difficulty of hitting different sized shooting targets at different distances. When using a scope with both mrad adjustment and a reticle with mrad markings (called an "mrad/mrad scope"), the shooter can use the reticle as a ruler to count the number of mrads a shot was off-target, which directly translates to the sight adjustment needed to hit the target with a follow up shot. Optics with mrad markings in the reticle can also be used to make a range estimation of a known size target, or vice versa, to determine a target size if the distance is known, a practice called "milling". Milliradian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reticle
A reticle, or reticule also known as a graticule, is a pattern of fine lines or markings built into the eyepiece of an optical device such as a telescopic sight, spotting scope, theodolite, optical microscope or the screen of an oscilloscope, to provide measurement references during visual inspections. Today, engraved lines or embedded fibers may be replaced by a digital image superimposed on a screen or eyepiece. Both terms may be used to describe any set of patterns used for aiding visual measurements and calibrations, but in modern use ''reticle'' is most commonly used for weapon sights, while ''graticule'' is more widely used for non-weapon measuring instruments such as oscilloscope display, astronomic telescopes, microscopes and slides, surveying instruments and other similar devices. There are many variations of reticle pattern; this article concerns itself mainly with the most rudimentary reticle: the crosshair. Crosshairs are typically represented as a pair of perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine and cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
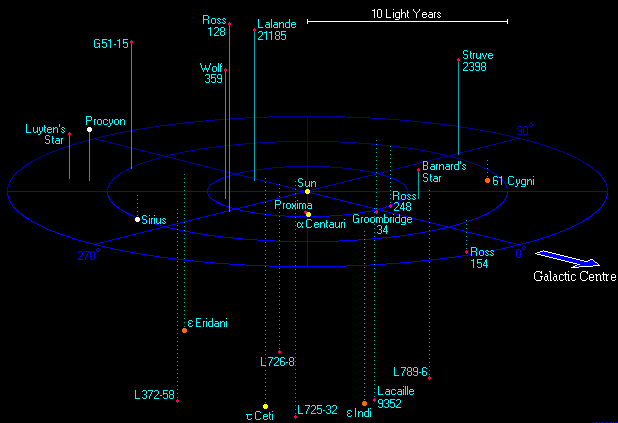
Light Year
A light-year, alternatively spelled light year, is a large unit of length used to express astronomical distances and is equivalent to about 9.46 trillion kilometers (), or 5.88 trillion miles ().One trillion here is taken to be 1012 (one million million, or billion in long scale). As defined by the International Astronomical Union (IAU), a light-year is the distance that light travels in a vacuum in one Julian year (365.25 days). Because it includes the time-measurement word "year", the term ''light-year'' is sometimes misinterpreted as a unit of time. The ''light-year'' is most often used when expressing distances to stars and other distances on a galactic scale, especially in non-specialist contexts and popular science publications. The unit most commonly used in professional astronomy is the parsec (symbol: pc, about 3.26 light-years) which derives from astrometry; it is the distance at which one astronomical unit subtends an angle of one second of arc. Defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parsec
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to or (au), i.e. . The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 au subtends an angle of one arcsecond ( of a degree). This corresponds to astronomical units, i.e. 1\, \mathrm = 1/\tan \left( \ \mathrm \right)\, \mathrm. The nearest star, Proxima Centauri, is about from the Sun. Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand. The word ''parsec'' is a portmanteau of "parallax of one second" and was coined by the British astronomer Herbert Hall Turner in 1913 to make calculations of astronomical distances from only raw observational data easy for astronomers. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arcsecond
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth circumference is very near . A minute of arc is of a radian. A second of arc, arcsecond (arcsec), or arc second, denoted by the symbol , is of an arcminute, of a degree, of a turn, and (about ) of a radian. These units originated in Babylonian astronomy as sexagesimal subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship. To express even smaller angles, standard SI prefixes can be employed; the milliarcsecond (mas) and microarcsecond (μas), for instance, are commonly used in astron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Unit
The astronomical unit (symbol: au, or or AU) is a unit of length, roughly the distance from Earth to the Sun and approximately equal to or 8.3 light-minutes. The actual distance from Earth to the Sun varies by about 3% as Earth orbits the Sun, from a maximum (aphelion) to a minimum (perihelion) and back again once each year. The astronomical unit was originally conceived as the average of Earth's aphelion and perihelion; however, since 2012 it has been defined as exactly (see below for several conversions). The astronomical unit is used primarily for measuring distances within the Solar System or around other stars. It is also a fundamental component in the definition of another unit of astronomical length, the parsec. History of symbol usage A variety of unit symbols and abbreviations have been in use for the astronomical unit. In a 1976 resolution, the International Astronomical Union (IAU) had used the symbol ''A'' to denote a length equal to the astronomical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.png)
