|
Structural Equivalence
Similarity in network analysis occurs when two nodes (or other more elaborate structures) fall in the same equivalence class. There are three fundamental approaches to constructing measures of network similarity: structural equivalence, automorphic equivalence, and regular equivalence.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. There is a hierarchy of the three equivalence concepts: any set of structural equivalences are also automorphic and regular equivalences. Any set of automorphic equivalences are also regular equivalences. Not all regular equivalences are necessarily automorphic or structural; and not all automorphic equivalences are necessarily structural. Visualizing similarity and distance Clustering tools Agglomerative Hierarchical clustering of nodes on the basis of the similarity of their profiles of ties to other nodes provides a joining tree or Dendrogram that visualizes the degree of similarity among cases - and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchical Clustering
In data mining and statistics, hierarchical clustering (also called hierarchical cluster analysis or HCA) is a method of cluster analysis that seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two categories: * Agglomerative: This is a " bottom-up" approach: Each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy. * Divisive: This is a "top-down" approach: All observations start in one cluster, and splits are performed recursively as one moves down the hierarchy. In general, the merges and splits are determined in a greedy manner. The results of hierarchical clustering are usually presented in a dendrogram. The standard algorithm for hierarchical agglomerative clustering (HAC) has a time complexity of \mathcal(n^3) and requires \Omega(n^2) memory, which makes it too slow for even medium data sets. However, for some special cases, optimal efficient agglomerative methods (of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
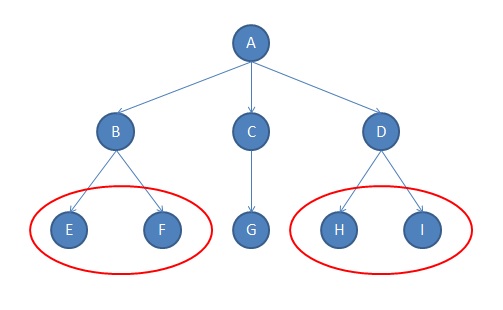
Dendrogram
A dendrogram is a diagram representing a tree. This diagrammatic representation is frequently used in different contexts: * in hierarchical clustering, it illustrates the arrangement of the clusters produced by the corresponding analyses. * in computational biology, it shows the clustering of genes or samples, sometimes in the margins of heatmaps. * in phylogenetics, it displays the evolutionary relationships among various biological taxa. In this case, the dendrogram is also called a phylogenetic tree. The name ''dendrogram'' derives from the two ancient greek words (), meaning "tree", and (), meaning "drawing, mathematical figure". Clustering example For a clustering example, suppose that five taxa (a to e) have been clustered by UPGMA based on a matrix of genetic distances. The hierarchical clustering dendrogram would show a column of five nodes representing the initial data (here individual taxa), and the remaining nodes represent the clusters to which the dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Equivalence
Similarity in network analysis occurs when two nodes (or other more elaborate structures) fall in the same equivalence class. There are three fundamental approaches to constructing measures of network similarity: structural equivalence, automorphic equivalence, and regular equivalence.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. There is a hierarchy of the three equivalence concepts: any set of structural equivalences are also automorphic and regular equivalences. Any set of automorphic equivalences are also regular equivalences. Not all regular equivalences are necessarily automorphic or structural; and not all automorphic equivalences are necessarily structural. Visualizing similarity and distance Clustering tools Agglomerative Hierarchical clustering of nodes on the basis of the similarity of their profiles of ties to other nodes provides a joining tree or Dendrogram that visualizes the degree of similarity among cases - and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine Similarity
In data analysis, cosine similarity is a measure of similarity between two sequences of numbers. For defining it, the sequences are viewed as vectors in an inner product space, and the cosine similarity is defined as the cosine of the angle between them, that is, the dot product of the vectors divided by the product of their lengths. It follows that the cosine similarity does not depend on the magnitudes of the vectors, but only on their angle. The cosine similarity always belongs to the interval 1, 1 For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. The cosine similarity is particularly used in positive space, where the outcome is neatly bounded in ,1/math>. For example, in information retrieval and text mining, each word is assigned a different coordinate and a document is represented by the vector of the numbers of occurrences of each word in the document. Cosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity Measure
In statistics and related fields, a similarity measure or similarity function or similarity metric is a real-valued function that quantifies the similarity between two objects. Although no single definition of a similarity exists, usually such measures are in some sense the inverse of distance metrics: they take on large values for similar objects and either zero or a negative value for very dissimilar objects. Though, in more broad terms, a similarity function may also satisfy metric axioms. Cosine similarity is a commonly used similarity measure for real-valued vectors, used in (among other fields) information retrieval to score the similarity of documents in the vector space model. In machine learning, common kernel functions such as the RBF kernel can be viewed as similarity functions. Use in clustering In spectral clustering, a similarity, or affinity, measure is used to transform data to overcome difficulties related to lack of convexity in the shape of the data distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automorphic Equivalence
Similarity in network analysis occurs when two nodes (or other more elaborate structures) fall in the same equivalence class. There are three fundamental approaches to constructing measures of network similarity: structural equivalence, automorphic equivalence, and regular equivalence.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. There is a hierarchy of the three equivalence concepts: any set of structural equivalences are also automorphic and regular equivalences. Any set of automorphic equivalences are also regular equivalences. Not all regular equivalences are necessarily automorphic or structural; and not all automorphic equivalences are necessarily structural. Visualizing similarity and distance Clustering tools Agglomerative Hierarchical clustering of nodes on the basis of the similarity of their profiles of ties to other nodes provides a joining tree or Dendrogram that visualizes the degree of similarity among cases - and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Equivalence
Similarity in network analysis occurs when two nodes (or other more elaborate structures) fall in the same equivalence class. There are three fundamental approaches to constructing measures of network similarity: structural equivalence, automorphic equivalence, and regular equivalence.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. There is a hierarchy of the three equivalence concepts: any set of structural equivalences are also automorphic and regular equivalences. Any set of automorphic equivalences are also regular equivalences. Not all regular equivalences are necessarily automorphic or structural; and not all automorphic equivalences are necessarily structural. Visualizing similarity and distance Clustering tools Agglomerative Hierarchical clustering of nodes on the basis of the similarity of their profiles of ties to other nodes provides a joining tree or Dendrogram that visualizes the degree of similarity among cases - and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity Measure
In statistics and related fields, a similarity measure or similarity function or similarity metric is a real-valued function that quantifies the similarity between two objects. Although no single definition of a similarity exists, usually such measures are in some sense the inverse of distance metrics: they take on large values for similar objects and either zero or a negative value for very dissimilar objects. Though, in more broad terms, a similarity function may also satisfy metric axioms. Cosine similarity is a commonly used similarity measure for real-valued vectors, used in (among other fields) information retrieval to score the similarity of documents in the vector space model. In machine learning, common kernel functions such as the RBF kernel can be viewed as similarity functions. Use in clustering In spectral clustering, a similarity, or affinity, measure is used to transform data to overcome difficulties related to lack of convexity in the shape of the data distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blockmodeling
Blockmodeling is a set or a coherent framework, that is used for analyzing social structure and also for setting procedure(s) for partitioning (clustering) social network's units (nodes, vertices, actors), based on specific patterns, which form a distinctive structure through interconnectivity.Patrick Doreian, An Intuitive Introduction to Blockmodeling with Examples, ''BMS: Bulletin of Sociological Methodology'' / ''Bulletin de Méthodologie Sociologique'', January, 1999, No. 61 (January, 1999), pp. 5–34. It is primarily used in statistics, machine learning and network science. As an empirical procedure, blockmodeling assumes that all the units in a specific network can be grouped together to such extent to which they are equivalent. Regarding equivalency, it can be structural, regular or generalized.Anuška Ferligoj: Blockmodeling, http://mrvar.fdv.uni-lj.si/sola/info4/nusa/doc/blockmodeling-2.pdf Using blockmodeling, a network can be analyzed using newly created blockmodels, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
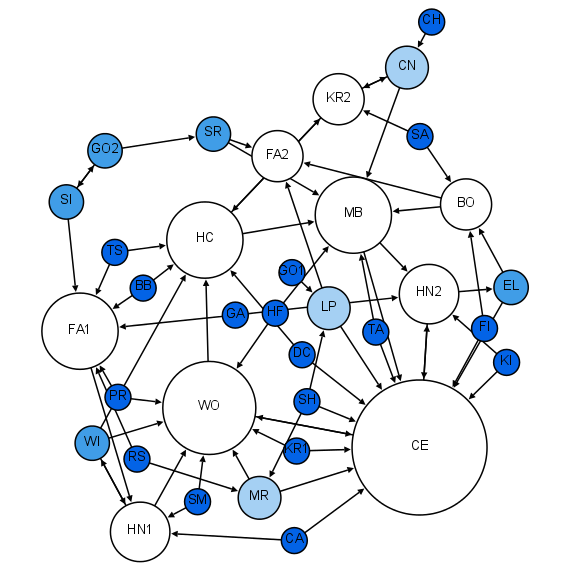
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
