|
Stability Criterion
In control theory, and especially stability theory, a stability criterion establishes when a system is stable. A number of stability criteria are in common use: * Circle criterion * Jury stability criterion *Liénard–Chipart criterion * Nyquist stability criterion *Routh–Hurwitz stability criterion *Vakhitov–Kolokolov stability criterion *Barkhausen stability criterion Stability may also be determined by means of root locus analysis. Although the concept of stability is general, there are several narrower definitions through which it may be assessed: * BIBO stability * Linear stability * Lyapunov stability * Orbital stability In mathematical physics and the theory of partial differential equations, the solitary wave solution of the form u(x,t)=e^\phi(x) is said to be orbitally stable if any solution with the initial data sufficiently close to \phi(x) forever remains ... {{sia Stability theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
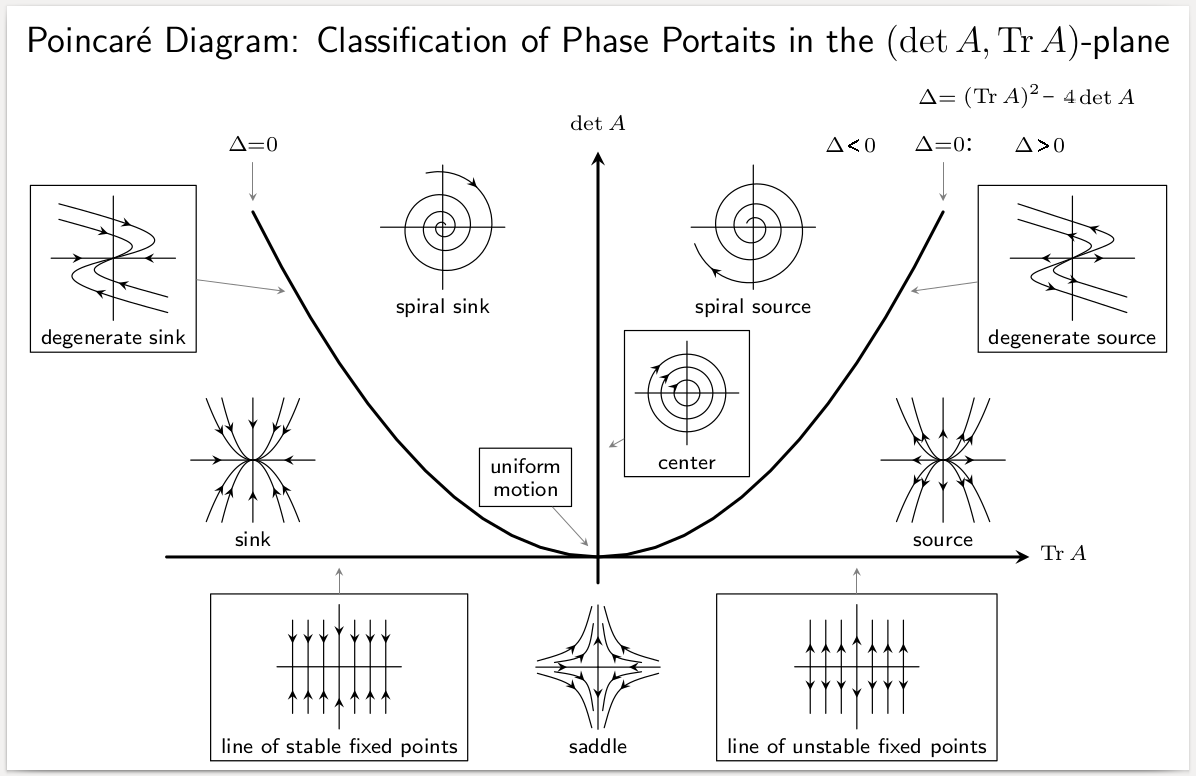
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance. In dynamical systems, an orbit is called '' Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem invol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Polynomial
In the context of the characteristic polynomial of a differential equation or difference equation, a polynomial is said to be stable if either: * all its roots lie in the open left half-plane, or * all its roots lie in the open unit disk. The first condition provides stability for continuous-time linear systems, and the second case relates to stability of discrete-time linear systems. A polynomial with the first property is called at times a Hurwitz polynomial and with the second property a Schur polynomial. Stable polynomials arise in control theory and in mathematical theory of differential and difference equations. A linear, time-invariant system (see LTI system theory) is said to be BIBO stable if every bounded input produces bounded output. A linear system is BIBO stable if its characteristic polynomial is stable. The denominator is required to be Hurwitz stable if the system is in continuous-time and Schur stable if it is in discrete-time. In practice, stability is determ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Criterion
In nonlinear control and stability theory, the circle criterion is a stability criterion for nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry ... for linear time-invariant (LTI) systems. Overview Consider a linear system subject to non-linear feedback, i.e. a non linear element \varphi(v, t) is present in the feedback loop. Assume that the element satisfies a sector condition mu_1,\mu_2/math>, and (to keep things simple) that the open loop system is stable. Then the closed loop system is globally asymptotically stable if the Nyquist locus does not penetrate the circle having as diameter the segment 1/\mu_1,-1/\mu_2/math> located on the ''x''-axis. General description Consider th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jury Stability Criterion
In signal processing and control theory, the Jury stability criterion is a method of determining the stability of a linear discrete time system by analysis of the coefficients of its characteristic polynomial. It is the discrete time analogue of the Routh–Hurwitz stability criterion. The Jury stability criterion requires that the system poles are located inside the unit circle centered at the origin, while the Routh-Hurwitz stability criterion requires that the poles are in the left half of the complex plane. The Jury criterion is named after Eliahu Ibraham Jury. Method If the characteristic polynomial of the system is given by :f(z) = a_n+a_z^1+a_z^2+\dots+a_1z^ + a_0z^n then the table is constructed as follows:Discrete-time control systems (2nd ed.), pg. 185. Prentice-Hall, Inc. Upper Saddle River, NJ, USA ©1995 That is, the first row is constructed of the polynomial coefficients in order, and the second row is the first row in reverse order and conjugated. The third ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liénard–Chipart Criterion
In control system theory, the Liénard–Chipart criterion is a stability criterion modified from the Routh–Hurwitz stability criterion, proposed by A. Liénard and M. H. Chipart. This criterion has a computational advantage over the Routh–Hurwitz criterion because it involves only about half the number of determinant computations. Algorithm The Routh–Hurwitz stability criterion says that a necessary and sufficient condition for all the roots of the polynomial with real coefficients ::f(z) = a_0 z^n + a_1 z^ + \cdots + a_n \, (a_0 > 0) to have negative real parts (i.e. f is Hurwitz stable A stable is a building in which livestock, especially horses, are kept. It most commonly means a building that is divided into separate stalls for individual animals and livestock. There are many different types of stables in use today; the ...) is that :: \Delta_1 > 0,\, \Delta_2 > 0, \ldots, \Delta_n > 0, where \Delta_i is the ''i''-th leading principal minor of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Stability Criterion
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a dynamical system. Because it only looks at the Nyquist plot of the open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system (although the number of each type of right-half-plane singularities must be known). As a result, it can be applied to systems defined by non-rational functions, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with multiple inputs and multiple outputs, such as control systems for airpla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Routh–Hurwitz Stability Criterion
In control system theory, the Routh–Hurwitz stability criterion is a mathematical test that is a necessary and sufficient condition for the stability of a linear time-invariant (LTI) dynamical system or control system. A stable system is one whose output signal is bounded; the position, velocity or energy do not increase to infinity as time goes on. The Routh test is an efficient recursive algorithm that English mathematician Edward John Routh proposed in 1876 to determine whether all the roots of the characteristic polynomial of a linear system have negative real parts. German mathematician Adolf Hurwitz independently proposed in 1895 to arrange the coefficients of the polynomial into a square matrix, called the Hurwitz matrix, and showed that the polynomial is stable if and only if the sequence of determinants of its principal submatrices are all positive. The two procedures are equivalent, with the Routh test providing a more efficient way to compute the Hurwitz determinan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vakhitov–Kolokolov Stability Criterion
The Vakhitov–Kolokolov stability criterion is a condition for linear stability (sometimes called ''spectral stability'') of solitary wave solutions to a wide class of U(1)-invariant Hamiltonian systems, named after Soviet scientists Aleksandr Kolokolov (Александр Александрович Колоколов) and Nazib Vakhitov (Назиб Галиевич Вахитов). The condition for linear stability of a solitary wave u(x,t) = \phi_\omega(x)e^ with frequency \omega has the form : \fracQ(\omega)<0, where is the (or momentum) of the solitary wave , conserved by |
Barkhausen Stability Criterion
In electronics, the Barkhausen stability criterion is a mathematical condition to determine when a linear electronic circuit will oscillate. It was put forth in 1921 by German physicist Heinrich Georg Barkhausen (1881–1956). It is widely used in the design of electronic oscillators, and also in the design of general negative feedback circuits such as op amps, to prevent them from oscillating. Limitations Barkhausen's criterion applies to linear circuits with a feedback loop. It cannot be applied directly to active elements with negative resistance like tunnel diode oscillators. The kernel of the criterion is that a complex pole pair must be placed on the imaginary axis of the complex frequency plane if steady state oscillations should take place. In the real world, it is impossible to balance on the imaginary axis, so in practice a steady-state oscillator is a non-linear circuit: * It needs to have positive feedback. * The loop gain is at unity (, \beta A, = 1\, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Locus
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex ''s''-plane as a function of a gain parameter (see pole–zero plot). An analog computer called a "Spirule" can compute root loci. Uses In addition to determining the stability of the system, the root locus can be used to design the damping ratio (''ζ'') and natural frequency (''ω''''n'') of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant natural frequency can be drawn as arccosine whose center points coincide with the origin. By selecting a point along ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
BIBO Stability
In signal processing, specifically control theory, bounded-input, bounded-output (BIBO) stability is a form of stability for signals and systems that take inputs. If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded. A signal is bounded if there is a finite value B > 0 such that the signal magnitude never exceeds B, that is :For discrete-time signals: \ , y \leq B \quad \text n \in \mathbb. :For continuous-time signals: \ , y(t), \leq B \quad \text t \in \mathbb. Time-domain condition for linear time-invariant systems Continuous-time necessary and sufficient condition For a continuous time linear time-invariant (LTI) system, the condition for BIBO stability is that the impulse response, h(t) , be absolutely integrable, i.e., its L1 norm exists. : \int_^\infty \left, h(t)\\,\mathordt = \, h \, _1 and the output \ y /math> is :\ y = h * x /math> where * denotes convolution. Then it follows by the definition of convol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |