|
Solar Hour
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Two types of solar time are apparent solar time (sundial time) and mean solar time (clock time). Introduction A tall pole vertically fixed in the ground casts a shadow on any sunny day. At one moment during the day, the shadow will point exactly north or south (or disappear when and if the Sun moves directly overhead). That instant is local apparent noon, or 12:00 local apparent time. About 24 hours later the shadow will again point north–south, the Sun seeming to have covered a 360-degree arc around Earth's axis. When the Sun has covered exactly 15 degrees (1/24 of a circle, both angles being measured in a plane perpendicular to Earth's axis), local apparent time is 13:00 exactly; after 15 more degrees it will be 14:00 exactly. The problem is that in September the Sun takes less time (as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sidereal Day (prograde)
Sidereal time (as a unit also sidereal day or sidereal rotation period) (sidereal ) is a timekeeping system that astronomers use to locate celestial objects. Using sidereal time, it is possible to easily point a telescope to the proper coordinates in the night sky. In short, sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars", or more correctly, relative to the March equinox. Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same sidereal time. This is similar to how the time kept by a sundial (Solar time) can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both Solar time and sidereal time make use of the regularity of Earth's rotation about its polar axis: solar time following the Sun while, roughly speaking, sidereal time follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Motion
In orbital mechanics, mean motion (represented by ''n'') is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit. Mean motion is used as an approximation of the actual orbital speed in making an initial calculation of the body's position in its orbit, f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equinox
A solar equinox is a moment in time when the Sun crosses the Earth's equator, which is to say, appears directly above the equator, rather than north or south of the equator. On the day of the equinox, the Sun appears to rise "due east" and set "due west". This occurs twice each year, around 20 March and 23 September. More precisely, an equinox is traditionally defined as the time when the plane of Earth's equator passes through the geometric center of the Sun's disk. Equivalently, this is the moment when Earth's rotation axis is directly perpendicular to the Sun-Earth line, tilting neither toward nor away from the Sun. In modern times, since the Moon (and to a lesser extent the planets) causes Earth's orbit to vary slightly from a perfect ellipse, the equinox is officially defined by the Sun's more regular ecliptic longitude rather than by its declination. The instants of the equinoxes are currently defined to be when the apparent geocentric longitude of the Sun is 0° a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. This plane of reference bases the equatorial coordinate system. In other words, the celestial equator is an abstract projection of the terrestrial equator into outer space. Due to Earth's axial tilt, the celestial equator is currently inclined by about 23.44° with respect to the ecliptic (the plane of Earth's orbit), but has varied from about 22.0° to 24.5° over the past 5 million years due to perturbation from other planets. An observer standing on Earth's equator visualizes the celestial equator as a semicircle passing through the zenith, the point directly overhead. As the observer moves north (or south), the celestial equator tilts towards the opposite horizon. The celestial equator is defined to be infinitely distant (since it is on the celestial sphere); thus, the ends of the semicircle always intersect the horizon due east and due west, regardless ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest circle that c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecliptic
The ecliptic or ecliptic plane is the orbital plane of the Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane and is the basis of the ecliptic coordinate system. Sun's apparent motion The ecliptic is the apparent path of the Sun throughout the course of a year. Because Earth takes one year to orbit the Sun, the apparent position of the Sun takes one year to make a complete circuit of the ecliptic. With slightly more than 365 days in one year, the Sun moves a little less than 1° eastward every day. This small difference in the Sun's position against the stars causes any particular spot on Earth's surface to catch up with (and stand directly north or south of) the Sun about four minutes later each day than it would if Earth did not orbit; a day on Earth is therefore 24 hours ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Tilt
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination. At an obliquity of 0 degrees, the two axes point in the same direction; that is, the rotational axis is perpendicular to the orbital plane. The rotational axis of Earth, for example, is the imaginary line that passes through both the North Pole and South Pole, whereas the Earth's orbital axis is the line perpendicular to the imaginary plane through which the Earth moves as it revolves around the Sun; the Earth's obliquity or axial tilt is the angle between these two lines. Earth's obliquity oscillates between 22.1 and 24.5 degrees on a 41,000-year cycle. Based on a continuously updated formula (here Laskar, 1986, though since 2006 the IMCCE and the IAU recommend the P03 model), Earth's mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aphelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass is negligible (e.g., f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass is negligible (e.g., f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
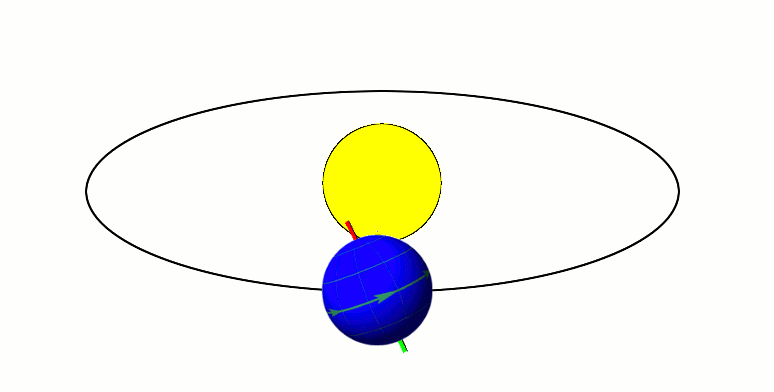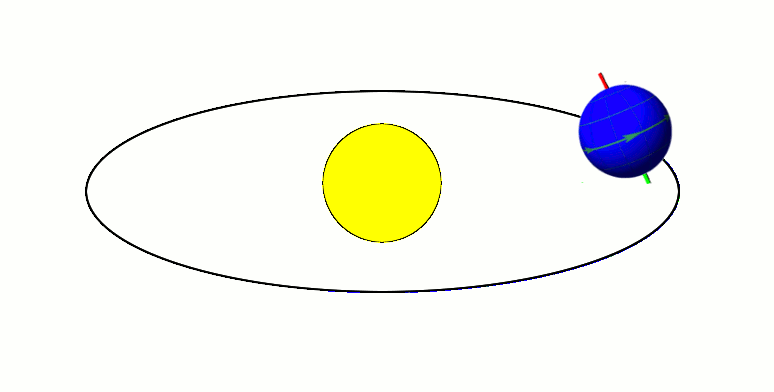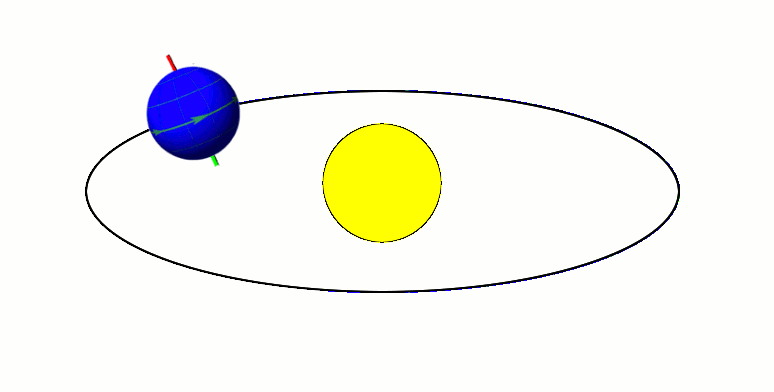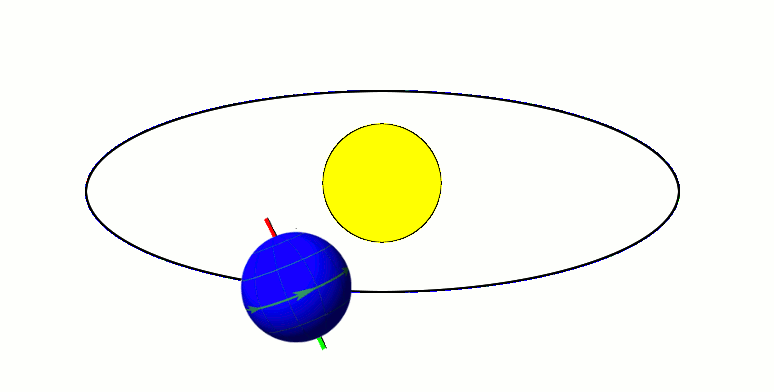
Earth's Orbit
Earth orbits the Sun at an average distance of 149.60 million km (92.96 million mi) in a counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes days (1 sidereal year), during which time Earth has traveled 940 million km (584 million mi). Jean Meeus, ''Astronomical Algorithms'' 2nd ed, (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough. Ignoring the influence of other Solar System bodies, Earth's orbit is an ellipse with the Earth-Sun barycenter as one focus and a current eccentricity of 0.0167. Since this value is close to zero, the center of the orbit is relatively close to the center of the Sun (relative to the size of the orbit). As seen from Earth, the planet's orbital prograde motion makes the Sun appear to move with respect to other stars at a rate of about 1° eastward per solar day (or a Sun or Moon diameter every 12 hours).Our planet takes about 36 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





.png)
