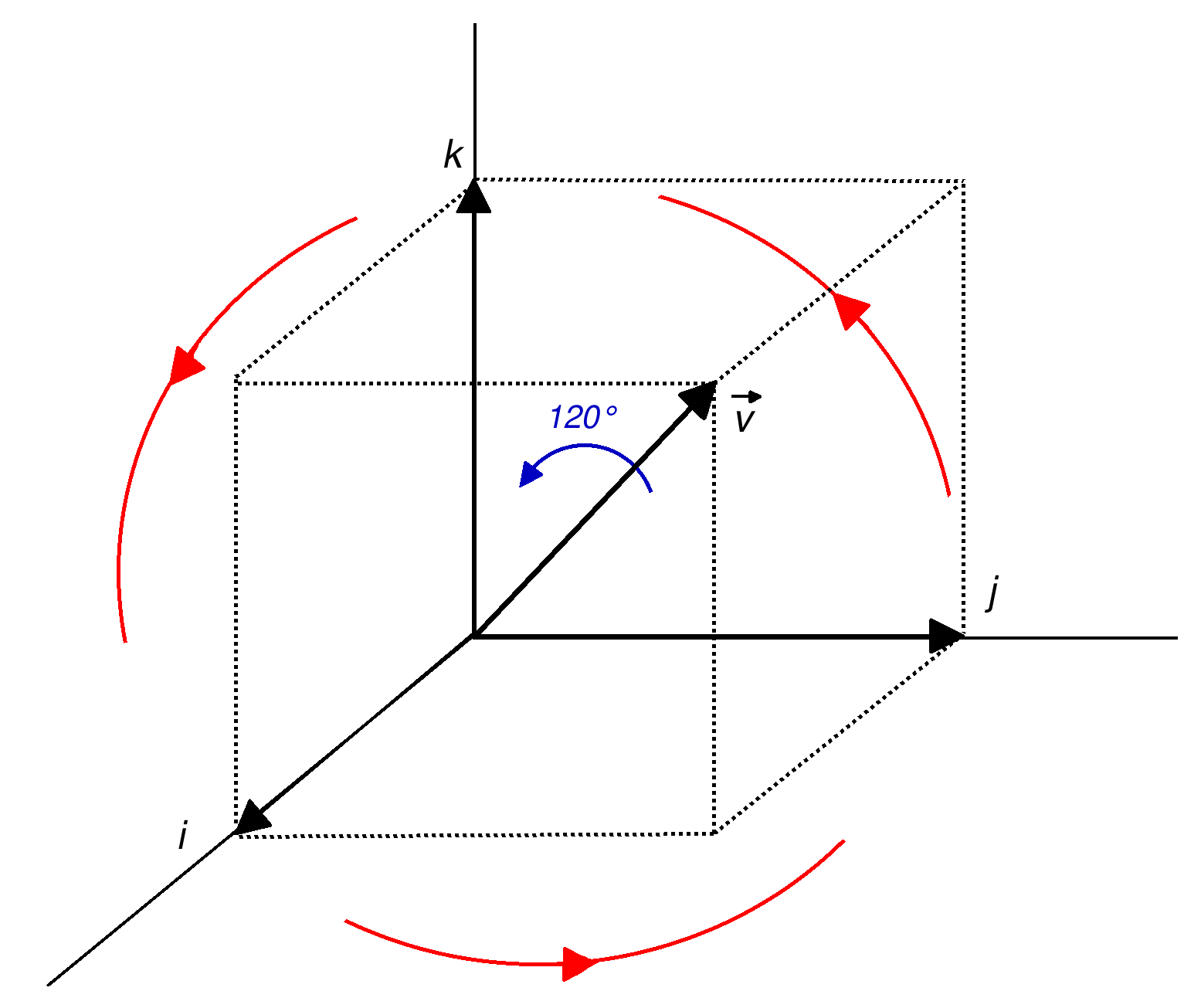
|
Slerp
In computer graphics, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion interpolation for the purpose of animation, animating 3D rotation. It refers to constant-speed motion along a unit-radius great circle arc, given the ends and an interpolation parameter between 0 and 1. Geometric Slerp Slerp has a geometric formula independent of quaternions, and independent of the dimension of the space in which the arc is embedded. This formula, a symmetric weighted sum credited to Glenn Davis, is based on the fact that any point on the curve must be a linear combination of the ends. Let ''p''0 and ''p''1 be the first and last points of the arc, and let ''t'' be the parameter, 0 ≤ ''t'' ≤ 1. Compute Ω as the angle Subtended angle, subtended by the arc, so that , the ''n''-dimensional dot product of the unit vectors from the origin to the ends. The geometric formula is then : \operatorname(p_0,p_1; t) = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternions And Spatial Rotation
Unit quaternions, known as ''versors'', provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, Presented at SIGGRAPH '85. computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis. When used to represent rotation, unit quaternions are also called rotation quaternions as they represent the 3D rotation group. When used to represent an orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. A spatial rotation around a fixed point of \theta radians about a unit axis (X,Y,Z) that denotes the ''Euler axis'' is given by the quaternion (C, X \, S, Y \, S, Z \, S), where C = \cos(\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great deal of specialized hardware and software has been developed, with the displays of most devices being driven by computer graphics hardware. It is a vast and recently developed area of computer science. The phrase was coined in 1960 by computer graphics researchers Verne Hudson and William Fetter of Boeing. It is often abbreviated as CG, or typically in the context of film as computer generated imagery (CGI). The non-artistic aspects of computer graphics are the subject of computer science research. Some topics in computer graphics include user interface design, sprite graphics, rendering, ray tracing, geometry processing, computer animation, vector graphics, 3D modeling, shaders, GPU design, implicit surfaces, visualization, scientific c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-parameter Subgroup
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphism :\varphi : \mathbb \rightarrow G from the real line \mathbb (as an additive group) to some other topological group G. If \varphi is injective then \varphi(\mathbb), the image, will be a subgroup of G that is isomorphic to \mathbb as an additive group. One-parameter groups were introduced by Sophus Lie in 1893 to define infinitesimal transformations. According to Lie, an ''infinitesimal transformation'' is an infinitely small transformation of the one-parameter group that it generates. It is these infinitesimal transformations that generate a Lie algebra that is used to describe a Lie group of any dimension. The action of a one-parameter group on a set is known as a flow. A smooth vector field on a manifold, at a point, induces a ''local flow'' - a one parameter group of local diffeomorphisms, sending points along integral curves of the vector field. The local flo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Transport
In geometry, parallel transport (or parallel translation) is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection (a covariant derivative or connection (vector bundle), connection on the tangent bundle), then this connection allows one to transport vectors of the manifold along curves so that they stay ''parallel'' with respect to the connection. The parallel transport for a connection thus supplies a way of, in some sense, moving the local geometry of a manifold along a curve: that is, of ''connecting'' the geometries of nearby points. There may be many notions of parallel transport available, but a specification of one — one way of connecting up the geometries of points on a curve — is tantamount to providing a ''connection''. In fact, the usual notion of connection is the infinitesimal analog of parallel transport. Or, ''vice versa'', parallel transport is the local realization of a conne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term "natural". The definition of the natural logarithm can then b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number : e^ = \cos x + i\sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus i sine"). The formula is still valid if is a complex number, and so some authors refer to the more general complex version as Euler's formula. Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes presented a geometrical ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Versor
In mathematics, a versor is a quaternion of norm one (a ''unit quaternion''). The word is derived from Latin ''versare'' = "to turn" with the suffix ''-or'' forming a noun from the verb (i.e. ''versor'' = "the turner"). It was introduced by William Rowan Hamilton in the context of his quaternion theory. Each versor has the form :q = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is a unit-length vector quaternion (or that the first component of r is zero, and the last three components of r are a unit vector in 3 dimensions). The corresponding 3-dimensional rotation has the angle 2''a'' about the axis r in axis–angle representation. In case (a right angle), then q = \mathbf, and the resulting unit vector is termed a ''right versor''. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U''q''. He was then able to display the general quaternion in polar coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Series
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''an'' represents the coefficient of the ''n''th term and ''c'' is a constant. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, ''c'' (the ''center'' of the series) is equal to zero, for instance when considering a Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. Beyond their role in mathematical analysis, power series also occur in combinatorics as generating functions (a kind of formal power series) and in electronic engineering (under the name of the Z-transform). The familiar decimal notation for real numbers can also be viewed as an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Numbers
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\[1ex] & = \underbrace_ \times \underbrace_ \\[1ex] & = b^n \times b^m \end In other words, when multiplying a base raised to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
