|
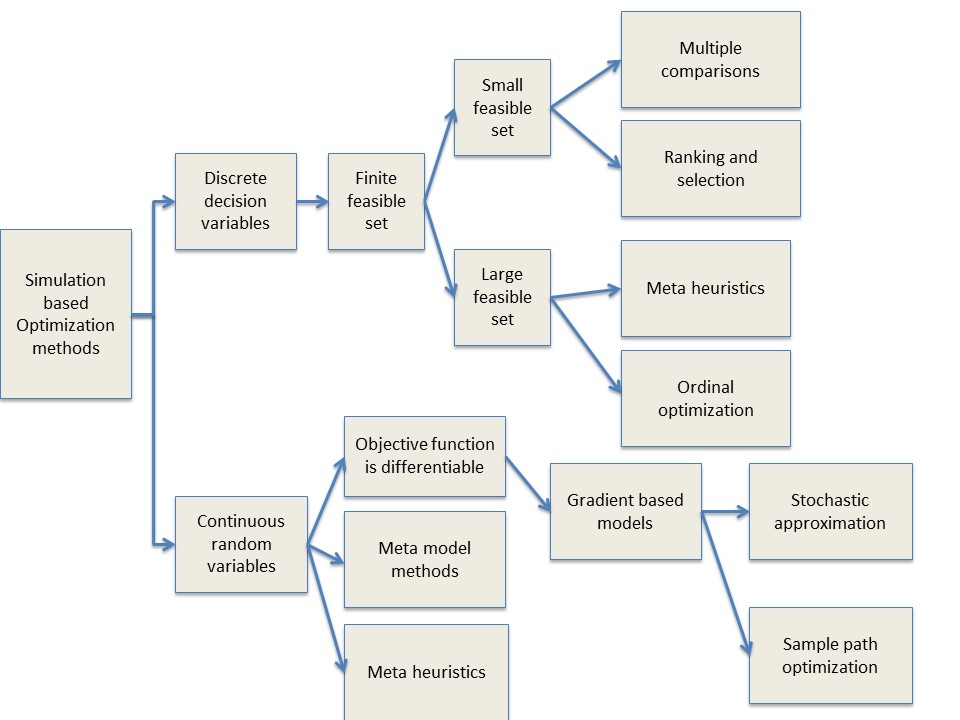
Simulation-based Optimisation
Simulation-based optimization (also known as simply simulation optimization) integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques (called output analysis in simulation methodology). Once a system is mathematically modeled, computer-based simulations provide information about its behavior. Parametric simulation methods can be used to improve the performance of a system. In this method, the input of each variable is varied with other parameters remaining constant and the effect on the design objective is observed. This is a time-consuming method and improves the performance partially. To obtain the optimal solution with minimum computation and time, the problem is solved iteratively where in each iteration th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization (mathematics)
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heuristic (computer Science)
A heuristic or heuristic technique (''problem solving'', ''Heuristic (psychology), mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a Pragmatism, pragmatic method that is not fully Mathematical optimisation, optimized, perfected, or Rationality, rationalized, but is nevertheless "good enough" as an approximation or attribute substitution. Where finding an optimal solution is impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution. Heuristics can be mental shortcuts that ease the cognitive load of Decision-making, making a decision. Context Gigerenzer & Gaissmaier (2011) state that Set (mathematics), sub-sets of ''strategy'' include heuristics, regression analysis, and Bayesian inference. Heuristics are strategies based on rules to generate optimal decisions, like the anchoring effect and utility maximization problem. These strategies depend on using readily accessible, thoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Tsitsiklis
John N. Tsitsiklis (; born 1958) is a Greek-American probabilist. He is the Clarence J. Lebel Professor of Electrical Engineering with the Department of Electrical Engineering and Computer Science (EECS) at the Massachusetts Institute of Technology. He serves as the director of the Laboratory for Information and Decision Systems and is affiliated with the Institute for Data, Systems, and Society (IDSS), the Statistics and Data Science Center and the MIT Operations Research Center. Education Tsitsiklis received a B.S. degree in Mathematics (1980), and his B.S. (1980), M.S. (1981), and Ph.D. (1984) degrees in Electrical Engineering, all from the Massachusetts Institute of Technology in Cambridge, Massachusetts. Awards and honors Tsitsiklis was elected to the 2007 class of Fellows of the Institute for Operations Research and the Management Sciences. He won the "2016 ACM SIGMETRICS Achievement Award in recognition of his fundamental contributions to decentralized control and cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of research in computer science that develops and studies methods and software that enable machines to machine perception, perceive their environment and use machine learning, learning and intelligence to take actions that maximize their chances of achieving defined goals. High-profile applications of AI include advanced web search engines (e.g., Google Search); recommendation systems (used by YouTube, Amazon (company), Amazon, and Netflix); virtual assistants (e.g., Google Assistant, Siri, and Amazon Alexa, Alexa); autonomous vehicles (e.g., Waymo); Generative artificial intelligence, generative and Computational creativity, creative tools (e.g., ChatGPT and AI art); and Superintelligence, superhuman play and analysis in strategy games (e.g., ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luis Nunes Vicente
Luis Nunes Vicente (born 1967) is an applied mathematician and optimizer who is known for his research work in Continuous Optimization and particularly in Derivative-Free Optimization. He is the Timothy J. Wilmott '80 Endowed Chair Professor and Department Chair of the Department of Industrial and Systems Engineering of Lehigh University. Education Luis Nunes Vicente was born in Coimbra, Portugal in 1967. He obtained a B.S. in Mathematics and Operations Research at the University of Coimbra in 1990. He continued his studies at Rice University, USA, earning a Ph.D. in Applied Mathematics in 1996. His Ph.D. dissertation, titled ''Trust-Region Interior-Point Algorithms for a Class of Nonlinear Programming Problems'', was supervised by John Dennis. Career From 1996 to 2018, Luis Nunes Vicente was a faculty member at the Department of Mathematics of the University of Coimbra, Portugal, becoming full professor in 2009. He held several visiting positions, namely at the IBM T.J. Wats ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Katya Scheinberg
Katya Scheinberg is a Russian-American applied mathematician known for her research in continuous optimization and particularly in derivative-free optimization. She is a professor in the School of Industrial and Systems Engineering at Georgia Institute of Technology. Education and career Scheinberg was born in Moscow. She completed a bachelor's and master's degree in computational mathematics and cybernetics at Moscow State University in 1992, and earned a Ph.D. in operations research at Columbia University in 1997. Her dissertation, ''Issues Related to Interior Point Methods for Linear and Semidefinite Programming'', was supervised by Donald Goldfarb. Scheinberg worked for IBM Research at the Thomas J. Watson Research Center from 1997 until 2009. After working as a research scientist at Columbia University and as an adjunct faculty member at New York University, she joined the Lehigh faculty in 2010. Scheinberg became Wagner Professor at Lehigh in 2014. In 2019 she moved to Cor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative-free Optimization
Derivative-free optimization (sometimes referred to as blackbox optimization) is a discipline in mathematical optimization that does not use derivative information in the classical sense to find optimal solutions: Sometimes information about the derivative of the objective function ''f'' is unavailable, unreliable or impractical to obtain. For example, ''f'' might be non-smooth, or time-consuming to evaluate, or in some way noisy, so that methods that rely on derivatives or approximate them via finite differences are of little use. The problem to find optimal points in such situations is referred to as derivative-free optimization, algorithms that do not use derivatives or finite differences are called derivative-free algorithms. Introduction The problem to be solved is to numerically optimize an objective function f\colon A\to\mathbb for some set A (usually A\subset\mathbb^n), i.e. find x_0\in A such that without loss of generality f(x_0)\leq f(x) for all x\in A. When applicable, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Approximation
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations. In a nutshell, stochastic approximation algorithms deal with a function of the form f(\theta) = \operatorname E_ (\theta,\xi) which is the expected value of a function depending on a random variable \xi . The goal is to recover properties of such a function f without evaluating it directly. Instead, stochastic approximation algorithms use random samples of F(\theta,\xi) to efficiently approximate properties of f such as zeros or extrema. Recently, stochastic approximations have found extensive applications in the fields of statistics and machine lea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genetic Algorithms
In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems via biologically inspired operators such as selection, crossover, and mutation. Some examples of GA applications include optimizing decision trees for better performance, solving sudoku puzzles, hyperparameter optimization, and causal inference. Methodology Optimization problems In a genetic algorithm, a population of candidate solutions (called individuals, creatures, organisms, or phenotypes) to an optimization problem is evolved toward better solutions. Each candidate solution has a set of properties (its chromosomes or genotype) which can be mutated and altered; traditionally, solutions are represented in binary as strings of 0s and 1s, but other encodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tabu Search
Tabu search (TS) is a metaheuristic search method employing local search methods used for mathematical optimization. It was created by Fred W. Glover in 1986 and formalized in 1989. Local (neighborhood) searches take a potential solution to a problem and check its immediate neighbors (that is, solutions that are similar except for very few minor details) in the hope of finding an improved solution. Local search methods have a tendency to become stuck in suboptimal regions or on plateaus where many solutions are equally fit. Tabu search enhances the performance of local search by relaxing its basic rule. First, at each step ''worsening'' moves can be accepted if no improving move is available (like when the search is stuck at a strict local minimum). In addition, ''prohibitions'' (hence the term ''tabu'') are introduced to discourage the search from coming back to previously-visited solutions. The implementation of tabu search uses memory structures that describe the visited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Response Surface Methodology
In statistics, response surface methodology (RSM) explores the relationships between several explanatory variables and one or more response variables. RSM is an empirical model which employs the use of mathematical and statistical techniques to relate input variables, otherwise known as factors, to the response. RSM became very useful because other methods available, such as the theoretical model, could be very cumbersome to use, time-consuming, inefficient, error-prone, and unreliable. The method was introduced by George E. P. Box and K. B. Wilson in 1951. The main idea of RSM is to use a sequence of designed experiments to obtain an optimal response. Box and Wilson suggest using a second-degree polynomial model to do this. They acknowledge that this model is only an approximation, but they use it because such a model is easy to estimate and apply, even when little is known about the process. Statistical approaches such as RSM can be employed to maximize the production of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |