|
Shifted Gompertz Distribution
The shifted Gompertz distribution is the distribution of the larger of two independent random variables one of which has an exponential distribution with parameter b and the other has a Gumbel distribution with parameters \eta and b . In its original formulation the distribution was expressed referring to the Gompertz distribution instead of the Gumbel distribution but, since the Gompertz distribution is a reverted Gumbel distribution, the labelling can be considered as accurate. It has been used as a model of Diffusion of innovations, adoption of innovations. It was proposed by Bemmaor (1994). Some of its statistical properties have been studied further by Jiménez and Jodrá (2009) and Jiménez Torres (2014). It has been used to predict the growth and decline of social networks and on-line services and shown to be superior to the Bass model and Weibull distribution (Bauckhage and Kristian Kersting, Kersting 2014). Specification Probability density function The probabilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kristian Kersting
Kristian Kersting (born November 28, 1973 in Cuxhaven, Germany) is a German computer scientist. He is Professor of Artificial intelligence and Machine Learning at the Department of Computer Science at the Technische Universität Darmstadt, Head of the Artificial Intelligence and Machine Learning Lab (AIML) and Co-Director of hessian.AI, the Hessian Center of Artificial Intelligence. He is known for his research on statistical relational artificial intelligence, probabilistic programming, and deep probabilistic learning. Life Kersting studied computer science at the University of Freiburg, where he received his Ph.D. in 2006. At the university he attended a course on artificial intelligence given by Bernhard Nebel and became interested in the topic. He was a visiting postdoctoral researcher at the Katholieke Universiteit Leuven and a postdoctoral associate at the Massachusetts Institute of Technology (MIT). His advisor at MIT was Leslie Pack Kaelbling. From 2008 to 2012, he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixture Model
In statistics, a mixture model is a probabilistic model for representing the presence of subpopulations within an overall population, without requiring that an observed data set should identify the sub-population to which an individual observation belongs. Formally a mixture model corresponds to the mixture distribution that represents the probability distribution of observations in the overall population. However, while problems associated with "mixture distributions" relate to deriving the properties of the overall population from those of the sub-populations, "mixture models" are used to make statistical inferences about the properties of the sub-populations given only observations on the pooled population, without sub-population identity information. Mixture models should not be confused with models for compositional data, i.e., data whose components are constrained to sum to a constant value (1, 100%, etc.). However, compositional models can be thought of as mixture models, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Extreme Value Distribution
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution needs to exist, which requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables. In some fields of application the generalized extreme value distribution is known as the Fisher–Tippett distribution, named after Ronald Fisher and L. H. C. Tippett who recognised three different forms outlined below. However usage of this name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bass Model
The Bass model or Bass diffusion model was developed by Frank Bass. It consists of a simple differential equation that describes the process of how new products get adopted in a population. The model presents a rationale of how current adopters and potential adopters of a new product interact. The basic premise of the model is that adopters can be classified as innovators or as imitators and the speed and timing of adoption depends on their degree of innovation and the degree of imitation among adopters. The Bass model has been widely used in forecasting, especially new products' sales forecasting and technology forecasting. Mathematically, the basic Bass diffusion is a Riccati equation with constant coefficients equivalent to Verhulst--Pearl Logistic growth. In 1969, Frank Bass published his paper on a new product growth model for consumer durables. Prior to this, Everett Rogers published ''Diffusion of Innovations'', a highly influential work that described the different stages o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
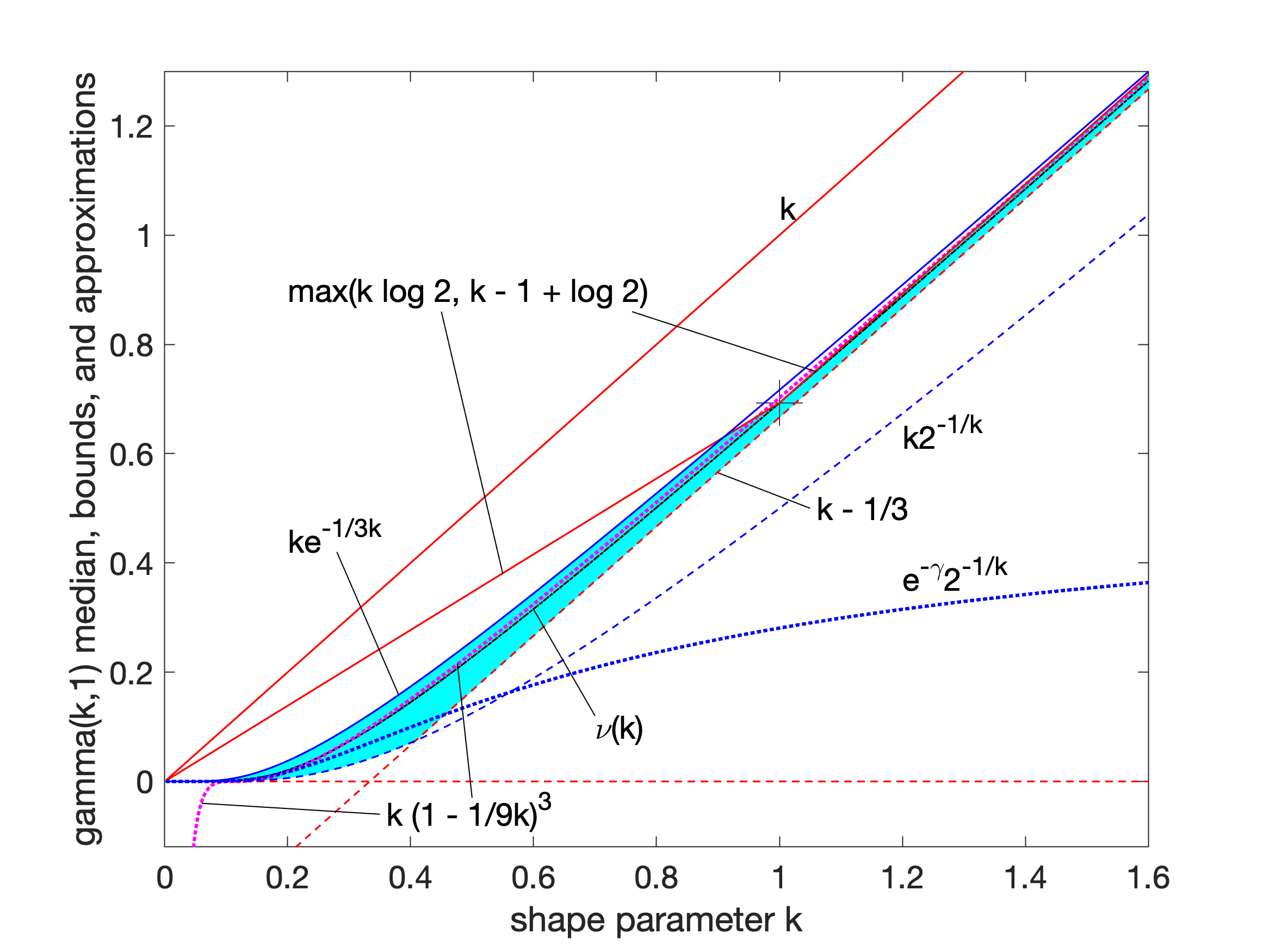
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by an ''upwards continuous'' ''monotonic increasing'' cumulative distribution function F : \mathbb R \rightarrow ,1/math> satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability that the random variable X takes on a value less tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Of Innovations
Diffusion of innovations is a theory that seeks to explain how, why, and at what rate new ideas and technology spread. Everett Rogers, a professor of communication studies, popularized the theory in his book ''Diffusion of Innovations''; the book was first published in 1962, and is now in its fifth edition (2003). Rogers argues that diffusion is the process by which an innovation is communicated over time among the participants in a social system. The origins of the diffusion of innovations theory are varied and span multiple disciplines. Rogers proposes that five main elements influence the spread of a new idea: the innovation itself, adopters, communication channels, time, and a social system. This process relies heavily on social capital. The innovation must be widely adopted in order to self-sustain. Within the rate of adoption, there is a point at which an innovation reaches critical mass. In 1989, management consultants working at the consulting firm Regis Mckenna Inc. the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gumbel Distribution
In probability theory and statistics, the Gumbel distribution (also known as the type-I generalized extreme value distribution) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions. This distribution might be used to represent the distribution of the maximum level of a river in a particular year if there was a list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur. The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory, which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type. ''This article uses the Gumbel distribution to model the distribution of the maximum value''. ''To model the minimum value, use the negative of the original values.'' The Gumbel distribution is a parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \lambda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |