|
Self Organizing Map
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional (typically two-dimensional) representation of a higher dimensional data set while preserving the topological structure of the data. For example, a data set with p variables measured in n observations could be represented as clusters of observations with similar values for the variables. These clusters then could be visualized as a two-dimensional "map" such that observations in proximal clusters have more similar values than observations in distal clusters. This can make high-dimensional data easier to visualize and analyze. An SOM is a type of artificial neural network but is trained using competitive learning rather than the error-correction learning (e.g., backpropagation with gradient descent) used by other artificial neural networks. The SOM was introduced by the Finnish professor Teuvo Kohonen in the 1980s and therefore is so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unsupervised Learning
Unsupervised learning is a type of algorithm that learns patterns from untagged data. The hope is that through mimicry, which is an important mode of learning in people, the machine is forced to build a concise representation of its world and then generate imaginative content from it. In contrast to supervised learning where data is tagged by an expert, e.g. tagged as a "ball" or "fish", unsupervised methods exhibit self-organization that captures patterns as probability densities or a combination of neural feature preferences encoded in the machine's weights and activations. The other levels in the supervision spectrum are reinforcement learning where the machine is given only a numerical performance score as guidance, and semi-supervised learning where a small portion of the data is tagged. Neural networks Tasks vs. methods Neural network tasks are often categorized as discriminative (recognition) or generative (imagination). Often but not always, discriminative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self Oraganizing Map Cartography
The self is an individual as the object of that individual’s own reflective consciousness. Since the ''self'' is a reference by a subject to the same subject, this reference is necessarily subjective. The sense of having a self—or ''selfhood''—should, however, not be confused with subjectivity itself. Ostensibly, this sense is directed outward from the subject to refer inward, back to its "self" (or itself). Examples of psychiatric conditions where such "sameness" may become broken include depersonalization, which sometimes occurs in schizophrenia: the self appears different from the subject. The first-person perspective distinguishes selfhood from personal identity. Whereas "identity" is (literally) sameness and may involve categorization and labeling, selfhood implies a first-person perspective and suggests potential uniqueness. Conversely, we use "person" as a third-person reference. Personal identity can be impaired in late-stage Alzheimer's disease and in other neu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
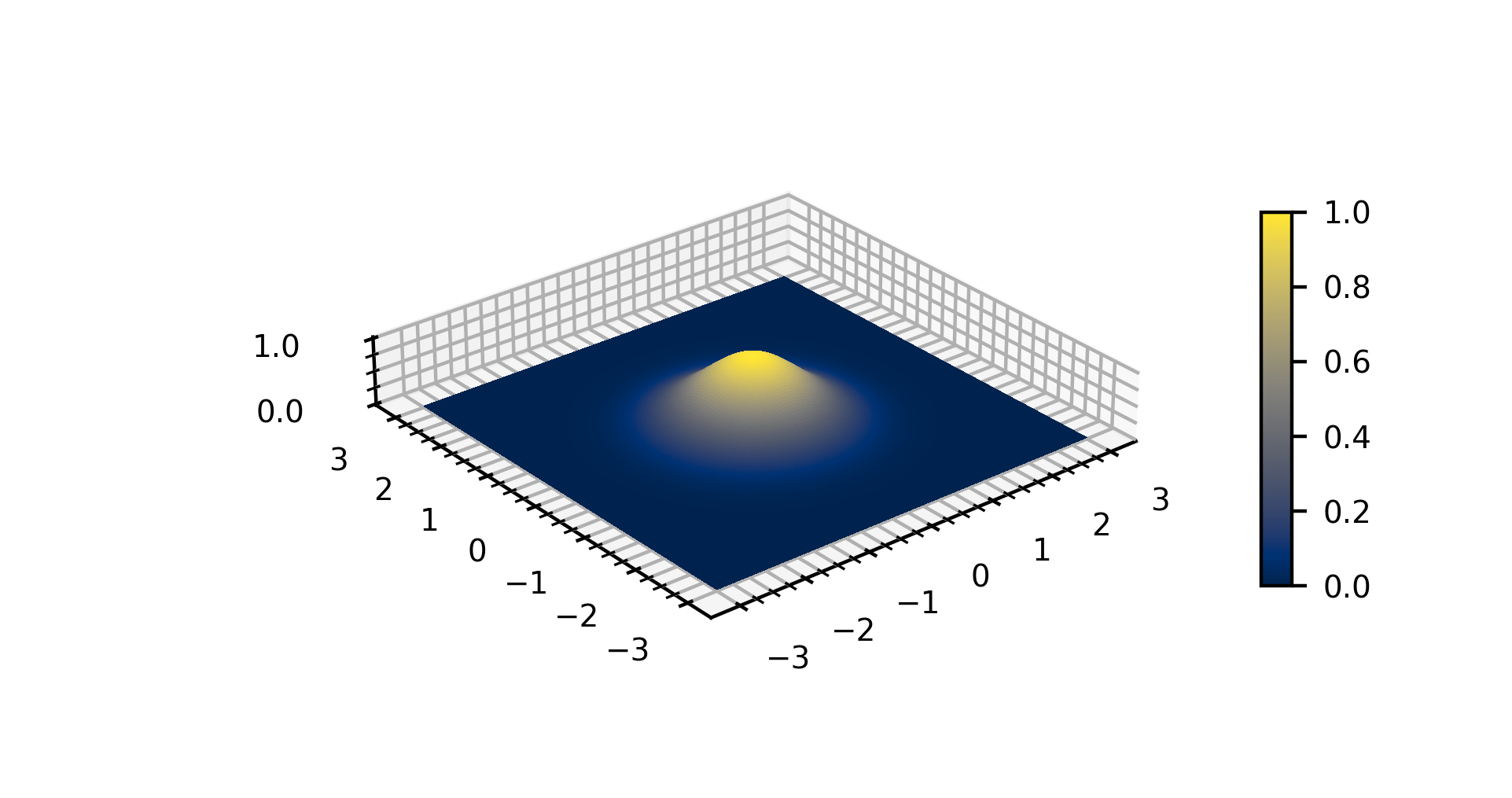
Mexican Hat Wavelet
In mathematics and numerical analysis, the Ricker wavelet :\psi(t) = \frac \left(1 - \left(\frac\right)^2 \right) e^ is the negative normalized second derivative of a Gaussian function, i.e., up to scale and normalization, the second Hermite function. It is a special case of the family of continuous wavelets (wavelets used in a continuous wavelet transform) known as Hermitian wavelets. The Ricker wavelet is frequently employed to model seismic data, and as a broad spectrum source term in computational electrodynamics. It is usually only referred to as the Mexican hat wavelet in the Americas, due to taking the shape of a sombrero when used as a 2D image processing kernel. It is also known as the Marr wavelet for David Marr. : \psi(x,y) = \frac\left(1-\frac \left(\frac\right)\right) e^ The multidimensional generalization of this wavelet is called the Laplacian of Gaussian function. In practice, this wavelet is sometimes approximated by the difference of Gaussians (DoG) funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a Gaussian is a characteristic symmetric " bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describe the normal distributions, in signal processing to define Gaussian filters, in image processing where two-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resampling (statistics)
In statistics, resampling is the creation of new samples based on one observed sample. Resampling methods are: # Permutation tests (also re-randomization tests) # Bootstrapping # Cross validation Permutation tests Permutation tests rely on resampling the original data assuming the null hypothesis. Based on the resampled data it can be concluded how likely the original data is to occur under the null hypothesis. Bootstrap Bootstrapping is a statistical method for estimating the sampling distribution of an estimator by sampling with replacement from the original sample, most often with the purpose of deriving robust estimates of standard errors and confidence intervals of a population parameter like a mean, median, proportion, odds ratio, correlation coefficient or regression coefficient. It has been called the plug-in principle,Logan, J. David and Wolesensky, Willian R. Mathematical methods in biology. Pure and Applied Mathematics: a Wiley-interscience Series of Texts, M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bootstrap Sampling
Bootstrapping is any test or metric that uses random sampling with replacement (e.g. mimicking the sampling process), and falls under the broader class of resampling methods. Bootstrapping assigns measures of accuracy (bias, variance, confidence intervals, prediction error, etc.) to sample estimates.software This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Bootstrapping estimates the properties of an (such as its ) by measuring those properties when sampling from an approximating distribution. One standard choice for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonically Decreasing
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is called ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Component
Principal may refer to: Title or rank * Principal (academia), the chief executive of a university ** Principal (education), the office holder/ or boss in any school * Principal (civil service) or principal officer, the senior management level in the UK Civil Service * Principal dancer, the top rank in ballet * Principal (music), the top rank in an orchestra Law * Principal (commercial law), the person who authorizes an agent ** Principal (architecture), licensed professional(s) with ownership of the firm * Principal (criminal law), the primary actor in a criminal offense * Principal (Catholic Church), an honorific used in the See of Lisbon Places * Principal, Cape Verde, a village * Principal, Ecuador, a parish Media * ''The Principal'' (TV series), a 2015 Australian drama series * ''The Principal'', a 1987 action film * Principal (music), the lead musician in a section of an orchestra * Principal photography, the first phase of movie production * "The Principal", a song on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |