|
Self-reference
Self-reference is a concept that involves referring to oneself or one's own attributes, characteristics, or actions. It can occur in language, logic, mathematics, philosophy, and other fields. In natural or formal languages, self-reference occurs when a sentence, idea or formula refers to itself. The reference may be expressed either directly—through some intermediate sentence or formula—or by means of some encoding. In philosophy, self-reference also refers to the ability of a subject to speak of or refer to itself, that is, to have the kind of thought expressed by the first person nominative singular pronoun "I" in English. Self-reference is studied and has applications in mathematics, philosophy, computer programming, second-order cybernetics, and linguistics, as well as in humor. Self-referential statements are sometimes paradoxical, and can also be considered recursive. In logic, mathematics and computing In classical philosophy, paradoxes were created b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ouroboros
The ouroboros or uroboros (; ) is an ancient symbol depicting a serpent symbolism, snake or European dragon, dragon Autocannibalism, eating its own tail. The ouroboros entered Western tradition via Egyptian mythology, ancient Egyptian iconography and the Greek Magical Papyri, Greek magical tradition. It was adopted as a symbol in Gnosticism and Hermeticism and, most notably, in alchemy. Some snakes, such as rat snakes, have been known to consume themselves. Name and interpretation The term derives , from ''oura'' 'tail' plus ''-boros'' '-eating'. The ''ouroboros'' is often interpreted as a symbol for eternal cyclic renewal or a Eternal return, cycle of life, death and rebirth; the snake's Sloughing, skin-sloughing symbolises the Metempsychosis, transmigration of souls. The snake biting its own tail is a fertility symbol in some religions: the tail is a Phallus, phallic symbol and the mouth is a yonic or womb-like symbol. Historical representations Ancient Egypt One ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paradoxes
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion. A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time. They result in "persistent contradiction between interdependent elements" leading to a lasting "unity of opposites". In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking, while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined. One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself and showed that attempts to found set theory on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-referential Humor
Self-referential humor, also known as self-reflexive humor, self-aware humor, or meta humor, is a type of comedic expression that—either directed toward some other subject, or openly directed toward itself—is self-referential in some way, intentionally alluding to the very person who is expressing the humor in a comedic fashion, or to some specific aspect of that same comedic expression. Here, ''meta'' is used to describe that the joke explicitly talks about other jokes, a usage similar to the words metadata (data about data), metatheatrics (a play within a play as in ''Hamlet'') and metafiction. Self-referential humor expressed discreetly and surrealistically is a form of bathos. In general, self-referential humor often uses hypocrisy, oxymoron, or paradox to create a contradictory or otherwise absurd situation that is humorous to the audience. History Old Comedy of Classical Athens is held to be the first—in the extant sources—form of self-referential comedy. Aristop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function (mathematics), function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur. A process that exhibits recursion is ''recursive''. Video feedback displays recursive images, as does an infinity mirror. Formal definitions In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties: * A simple ''base case'' (or cases) — a terminating scenario that does not use recursion to produce an answer * A ''recursive step'' — a set of rules that reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impredicativity
In mathematics, logic and philosophy of mathematics, something that is impredicative is a self-referencing definition. Roughly speaking, a definition is impredicative if it invokes (mentions or quantifies over) the set being defined, or (more commonly) another set that contains the thing being defined. There is no generally accepted precise definition of what it means to be predicative or impredicative. Authors have given different but related definitions. The opposite of impredicativity is predicativity, which essentially entails building stratified (or ramified) theories where quantification over a type at one 'level' results in types at a new, higher, level. A prototypical example is intuitionistic type theory, which retains ramification (without the explicit levels) so as to discard impredicativity. The 'levels' here correspond to the number of layers of dependency in a term definition. Russell's paradox is a famous example of an impredicative construction—namely the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
I (pronoun)
In Modern English, ''I'' is the singular, first-person pronoun. Morphology In Standard Modern English, ''I'' has five distinct word forms: * ''I'': the nominative (subjective) form **''I'' is the only pronoun form that is always capitalized in English. This practice became established in the late 15th century, though lowercase ''i'' was sometimes found as late as the 17th century. * ''me'': the accusative (objective, also called ' oblique') form * ''my:'' the dependent genitive (possessive) form * ''mine'': the independent genitive (possessive) form * ''myself'': the reflexive form History Old English had a first-person pronoun that inflected for four cases and three numbers. ''I'' originates from Old English (OE) , which had in turn originated from the continuation of Proto-Germanic , and ; the asterisk denotes an unattested form, but was attested in the Elder Futhark inscriptions (in some cases notably showing the variant ; see also ek erilaz). Linguists assume ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
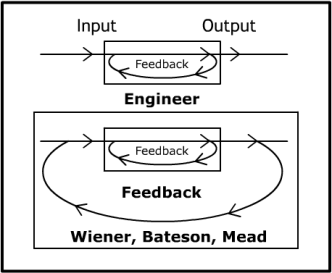
Second-order Cybernetics
Second-order cybernetics, also known as the cybernetics of cybernetics, is the recursive application of cybernetics to itself and the reflexive practice of cybernetics according to such a critique. It is cybernetics where "the role of the observer is appreciated and acknowledged rather than disguised, as had become traditional in western science".Ranulph Glanville, Glanville, R. (2002). "Second order cybernetics." In F. Parra-Luna (ed.), Systems science and cybernetics. In ''Encyclopaedia of Life Support Systems'' (EOLSS). OxfordEoLSS Second-order cybernetics was developed between the late 1960s and mid 1970s by Heinz von Foerster and others, with key inspiration coming from Margaret Mead. Foerster referred to it as "the control of control and the communication of communication" and differentiated first-order cybernetics as "the cybernetics of observed systems" and second-order cybernetics as "the cybernetics of observing systems".Heinz von Foerster, Foerster, Heinz von, ed. ''Cyber ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Berry's Paradox
The Berry paradox is a self-referential paradox arising from an expression like "The smallest positive integer not definable in under sixty letters" (a phrase with fifty-seven letters). Bertrand Russell, the first to discuss the paradox in print, attributed it to G. G. Berry (1867–1928), a junior librarian at Oxford's Bodleian Library. Russell called Berry "the only person in Oxford who understood mathematical logic". The paradox was called " Richard's paradox" by Jean-Yves Girard. Overview Consider the expression: Since there are only twenty-six letters in the English alphabet, there are finitely many phrases of under sixty letters, and hence finitely many positive integers that are defined by phrases of under sixty letters. Since there are infinitely many positive integers, this means that there are positive integers that cannot be defined by phrases of under sixty letters. If there are positive integers that satisfy a given property, then there is a ''smallest'' positi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Russell's Paradox
In mathematical logic, Russell's paradox (also known as Russell's antinomy) is a set-theoretic paradox published by the British philosopher and mathematician, Bertrand Russell, in 1901. Russell's paradox shows that every set theory that contains an unrestricted comprehension principle leads to contradictions. According to the unrestricted comprehension principle, for any sufficiently well-defined property, there is the set of all and only the objects that have that property. Let ''R'' be the set of all sets that are not members of themselves. (This set is sometimes called "the Russell set".) If ''R'' is not a member of itself, then its definition entails that it is a member of itself; yet, if it is a member of itself, then it is not a member of itself, since it is the set of all sets that are not members of themselves. The resulting contradiction is Russell's paradox. In symbols: : Let R = \. Then R \in R \iff R \not \in R. Russell also showed that a version of the paradox co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language is a set of strings whose symbols are taken from a set called "alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that can be parsed by machines with limited computational power. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |