|
S-wave
__NOTOC__ In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves. S waves are transverse waves, meaning that the direction of particle motion of a S wave is perpendicular to the direction of wave propagation, and the main restoring force comes from shear stress. Therefore, S waves cannot propagate in liquids with zero (or very low) viscosity; however, they may propagate in liquids with high viscosity. The name ''secondary wave'' comes from the fact that they are the second type of wave to be detected by an earthquake seismograph, after the compressional primary wave, or P wave, because S waves travel more slowly in solids. Unlike P waves, S waves cannot travel through the molten outer core of the Earth, and this causes a shadow zone fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. It also includes studies of earthquake environmental effects such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, glacial, fluvial, oceanic, atmospheric, and artificial processes such as explosions. A related field that uses geology to infer information regarding past earthquakes is paleoseismology. A recording of Earth motion as a function of time is called a seismogram. A seismologist is a scientist who does research in seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletus (c. 585 BCE), Anaximenes of Miletus (c. 550 BCE), Aristotle (c. 340 BCE), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shadow Zone
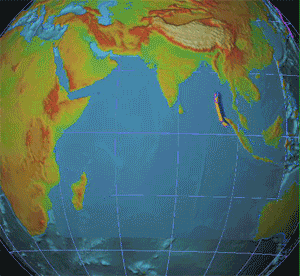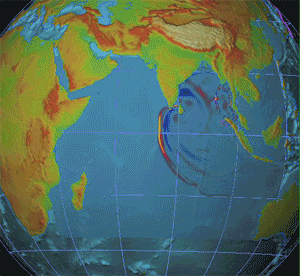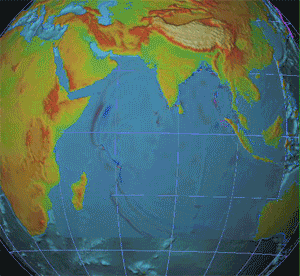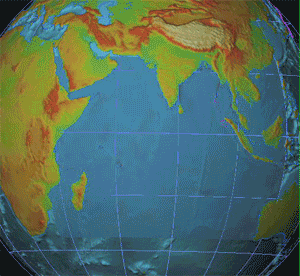
A seismic shadow zone is an area of the Earth's surface where seismographs cannot detect direct P waves and/or S waves from an earthquake. This is due to liquid layers or structures within the Earth's surface. The most recognized shadow zone is due to the core-mantle boundary where P waves are refracted and S waves are stopped at the liquid outer core; however, any liquid boundary or body can create a shadow zone. For example, magma reservoirs with a high enough percent melt can create seismic shadow zones. Background The earth is made up of different structures: the crust, the mantle, the inner core and the outer core. The crust, mantle, and inner core are typically solid; however, the outer core is entirely liquid. A liquid outer core was first shown in 1906 by Geologist Richard Oldham. Oldham observed seismograms from various earthquakes and saw that some seismic stations did not record direct S waves, particularly ones that were 120° away from the hypocenter of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P Wave
A P wave (primary wave or pressure wave) is one of the two main types of elastic body waves, called seismic waves in seismology. P waves travel faster than other seismic waves and hence are the first signal from an earthquake to arrive at any affected location or at a seismograph. P waves may be transmitted through gases, liquids, or solids. Nomenclature The name ''P wave'' can stand for either pressure wave (as it is formed from alternating compressions and rarefactions) or primary wave (as it has high velocity and is therefore the first wave to be recorded by a seismograph). The name '' S wave'' represents another seismic wave propagation mode, standing for secondary or shear wave. Seismic waves in the Earth Primary and secondary waves are body waves that travel within the Earth. The motion and behavior of both P and S waves in the Earth are monitored to probe the interior structure of the Earth. Discontinuities in velocity as a function of depth are indicative of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Elasticity
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics. The fundamental "linearizing" assumptions of linear elasticity are: infinitesimal strains or "small" deformations (or strains) and linear relationships between the components of stress and strain. In addition linear elasticity is valid only for stress states that do not produce yielding. These assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis. Mathematical formulation Equations governing a linear elastic boundary value problem are based on three tensor partial differential equations for the balance of linear momentum and six infinitesimal strain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Inner Core
Earth's inner core is the innermost geologic layer of planet Earth. It is primarily a solid ball with a radius of about , which is about 20% of Earth's radius or 70% of the Moon's radius. There are no samples of Earth's core accessible for direct measurement, as there are for Earth's mantle. Information about Earth's core mostly comes from analysis of seismic waves and Earth's magnetic field. The inner core is believed to be composed of an iron–nickel alloy with some other elements. The temperature at the inner core's surface is estimated to be approximately , which is about the temperature at the surface of the Sun. Scientific history Earth was discovered to have a solid inner core distinct from its molten outer core in 1936, by the Danish seismologist Inge Lehmann, who deduced its presence by studying seismograms from earthquakes in New Zealand. She observed that the seismic waves reflect off the boundary of the inner core and can be detected by sensitive seismographs o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Outer Core
Earth's outer core is a fluid layer about thick, composed of mostly iron and nickel that lies above Earth's solid inner core and below its mantle. The outer core begins approximately beneath Earth's surface at the core-mantle boundary and ends beneath Earth's surface at the inner core boundary. Properties Unlike Earth's solid, inner core, its outer core is liquid. Evidence for a fluid outer core includes seismology which shows that seismic shear-waves are not transmitted through the outer core. Although having a composition similar to Earth's solid inner core, the outer core remains liquid as there is not enough pressure to keep it in a solid state. Seismic inversions of body waves and normal modes constrain the radius of the outer core to be 3483 km with an uncertainty of 5 km, while that of the inner core is 1220±10 km. Estimates for the temperature of the outer core are about in its outer region and near the inner core. Modeling has shown that the outer core, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressional Wave
Longitudinal waves are waves in which the vibration of the medium is parallel ("along") to the direction the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal waves are also called ''compressional'' or compression waves, because they produce compression and rarefaction when traveling through a medium, and pressure waves, because they produce increases and decreases in pressure. A wave along the length of a stretched Slinky toy, where the distance between coils increases and decreases, is a good visualization. Real-world examples include sound waves (vibrations in pressure, a particle of displacement, and particle velocity propagated in an elastic medium) and seismic P-waves (created by earthquakes and explosions). The other main type of wave is the transverse wave, in which the displacements of the medium are at right angles to the direction of propagation. Transverse waves, for instance, describe ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Wave
In physics, a surface wave is a mechanical wave that propagates along the Interface (chemistry), interface between differing media. A common example is gravity waves along the surface of liquids, such as ocean waves. Gravity waves can also occur within liquids, at the interface between two fluids with different densities. Elastic surface waves can travel along the surface of solids, such as ''Rayleigh wave, Rayleigh'' or ''Love wave, Love'' waves. Electromagnetic waves can also propagate as "surface waves" in that they can be guided along with a refractive index gradient or along an interface between two media having different dielectric constants. In radio transmission (telecommunications), transmission, a ''ground wave'' is a guided wave that propagates close to the surface of the Earth. Mechanical waves In seismology, several types of surface waves are encountered. Surface waves, in this mechanical sense, are commonly known as either ''Love waves'' (L waves) or ''Rayleigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transverse Wave
In physics, a transverse wave is a wave whose oscillations are perpendicular to the direction of the wave's advance. This is in contrast to a longitudinal wave which travels in the direction of its oscillations. Water waves are an example of transverse wave. A simple example is given by the waves that can be created on a horizontal length of string by anchoring one end and moving the other end up and down. Another example is the waves that are created on the membrane of a drum. The waves propagate in directions that are parallel to the membrane plane, but each point in the membrane itself gets displaced up and down, perpendicular to that plane. Light is another example of a transverse wave, where the oscillations are the electric and magnetic fields, which point at right angles to the ideal light rays that describe the direction of propagation. Transverse waves commonly occur in elastic solids due to the shear stress generated; the oscillations in this case are the displa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's 2nd Law
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows: # A body remains at rest, or in motion at a constant speed in a straight line, unless acted upon by a force. # When a body is acted upon by a force, the time rate of change of its momentum equals the force. # If two bodies exert forces on each other, these forces have the same magnitude but opposite directions. The three laws of motion were first stated by Isaac Newton in his ''Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems, which laid the foundation for classical mechanics. In the time since Newton, the conceptual content of classical physics has been reformulated in alternative ways, involving different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain: :G \ \stackrel\ \frac = \frac = \frac where :\tau_ = F/A \, = shear stress :F is the force which acts :A is the area on which the force acts :\gamma_ = shear strain. In engineering :=\Delta x/l = \tan \theta , elsewhere := \theta :\Delta x is the transverse displacement :l is the initial length of the area. The derived SI unit of shear modulus is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or in thousand pounds per square inch (ksi). Its dimensional form is M1L−1T−2, replacing ''force'' by ''mass'' times ''acceleration''. Explanation The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law: * Young's modulus ''E'' describes t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |