|
Rotational Frequency
Rotational frequency (also known as rotational speed or rate of rotation) of an object rotating around an axis is the frequency of rotation of the object. Its unit is revolution per minute (rpm), cycle per second (cps), etc. The symbol for rotational frequency is \nu (the Greek lowercase letter nu). Tangential speed ''v'', rotational frequency \nu, and radial distance ''r'', are related by the following equation: :v = 2\pi r\nu :v = r\omega An algebraic rearrangement of this equation allows us to solve for rotational frequency: :\nu = v/2\pi r :\omega = v/r Thus, the tangential speed will be directly proportional to ''r'' when all parts of a system simultaneously have the same ''ω'', as for a wheel, disk, or rigid wand. The direct proportionality of ''v'' to ''r'' is not valid for the planets, because the planets have different rotational frequencies. Rotational frequency can measure, for example, how fast a motor is running. ''Rotational speed'' is sometimes used to m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Around A Fixed Axis
Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will appear. This article assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed direction, which is not true for ''free rotation of a rigid body''. The expressions for the kinetic energy of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Period
The rotation period of a celestial object (e.g., star, gas giant, planet, moon, asteroid) may refer to its sidereal rotation period, i.e. the time that the object takes to complete a single revolution around its axis of rotation relative to the background stars, measured in sidereal time. The other type of commonly used rotation period is the object's synodic rotation period (or ''solar day''), measured in solar time, which may differ by a fraction of a rotation or more than one rotation to accommodate the portion of the object's orbital period during one day. Measuring rotation For solid objects, such as rocky planets and asteroids, the rotation period is a single value. For gaseous or fluid bodies, such as stars and gas giants, the period of rotation varies from the object's equator to its pole due to a phenomenon called differential rotation. Typically, the stated rotation period for a gas giant (such as Jupiter, Saturn, Uranus, Neptune) is its internal rotation period, as d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Velocity
The radial velocity or line-of-sight velocity, also known as radial speed or range rate, of a target with respect to an observer is the temporal rate of change, rate of change of the distance or Slant range, range between the two points. It is equivalent to the vector projection of the target-observer relative velocity onto the relative direction (geometry), relative direction connecting the two points. In astronomy, the point is usually taken to be the observer on Earth, so the radial velocity then denotes the speed with which the object moves away from the Earth (or approaches it, for a negative radial velocity). Formulation Given a differentiable vector \mathbf \in \mathbb^3 defining the instantaneous position of a target relative to an observer. Let with \mathbf \in \mathbb^3, the instantaneous velocity of the target with respect to the observer. The magnitude of the position vector \mathbf is defined as The quantity range rate is the time derivative of the magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis). The magnitude of the pseudovector represents the ''angular speed'', the rate at which the object rotates or revolves, and its direction is normal to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.(EM1) There are two types of angular velocity. * Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. * Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
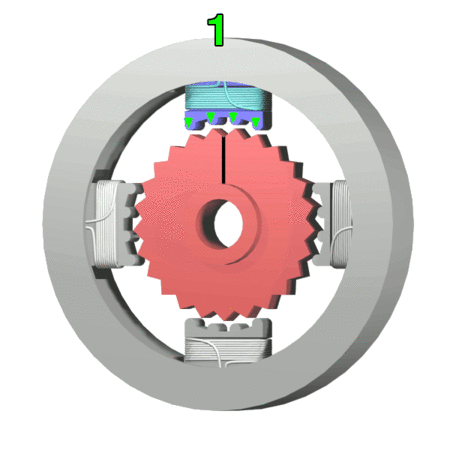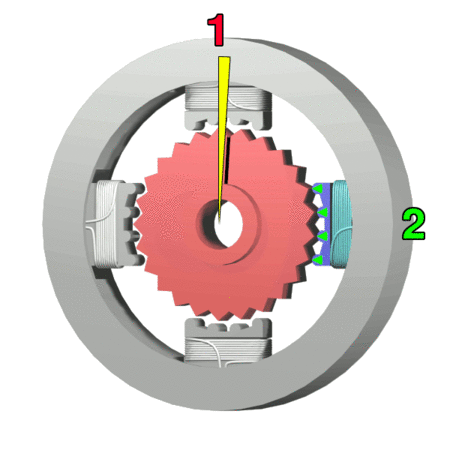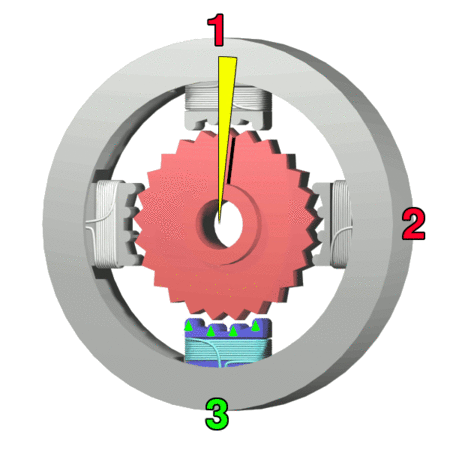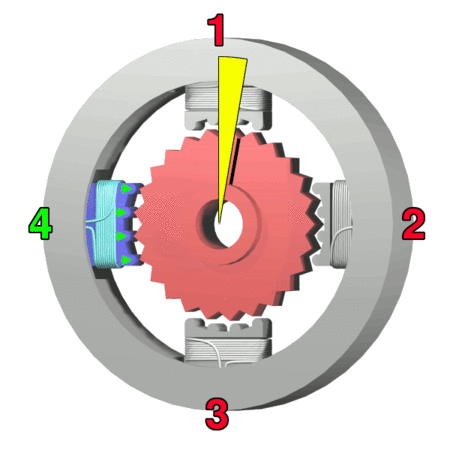
Stepper Motor
A stepper motor, also known as step motor or stepping motor, is a brushless DC electric motor that divides a full rotation into a number of equal steps. The motor's position can be commanded to move and hold at one of these steps without any position sensor for feedback (an open-loop controller), as long as the motor is correctly sized to the application in respect to torque and speed. Switched reluctance motors are very large stepping motors with a reduced pole count, and generally are closed-loop commutated. Mechanism Brushed DC motors rotate continuously when DC voltage is applied to their terminals. The stepper motor is known for its property of converting a train of input pulses (typically square waves) into a precisely defined increment in the shaft’s rotational position. Each pulse rotates the shaft through a fixed angle. Stepper motors effectively have multiple "toothed" electromagnets arranged as a stator around a central rotor, a gear-shaped piece of iron. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian Per Second
The radian per second (symbol: rad⋅s−1 or rad/s) is the unit of angular velocity in the International System of Units (SI). The radian per second is also the SI unit of angular frequency, commonly denoted by the Greek letter ''ω'' (omega). The radian per second is defined as the angular frequency that results in the angular displacement increasing by one radian every second. The angular frequency of one radian per second corresponds to a frequency of 1/(2) hertz (Hz), or cycles per second. This is because one cycle of rotation corresponds to an angular rotation of one turn (360 degrees), which equals 2 radians. Since the radian is a dimensionless unit in the SI, the radian per second is dimensionally equivalent to the hertz—both are defined as s−1. One radian per second also corresponds to about 9.55 revolutions per minute. : Coherent units A use of the unit radian per second is in calculation of the power transmitted by a shaft. In the International Syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by convention it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is equal to one event per second. The period is the interval of time between events, so the period is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times a minute (2 hertz), the period, —the interval at which the beats repeat—is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. Definitions and units For cyclical phenomena such as oscillations, waves, or for examples of simple harmonic motion, the term ''frequency'' is defined as the number of cycles or vibrations per unit of time. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a young protostar orbited by a protoplanetary disk. Planets grow in this disk by the gradual accumulation of material driven by gravity, a process called accretion. The Solar System has at least eight planets: the terrestrial planets Mercury, Venus, Earth and Mars, and the giant planets Jupiter, Saturn, Uranus and Neptune. These planets each rotate around an axis tilted with respect to its orbital pole. All of them possess an atmosphere, although that of Mercury is tenuous, and some share such features as ice caps, seasons, volcanism, hurricanes, tectonics, and even hydrology. Apart from Venus and Mars, the Solar System planets generate magnetic fields, and all except Venus and Mercury have natural satellites. The giant planets bear plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |