|
Risk Metric
In the context of risk measurement, a risk metric is the concept quantified by a risk measure. When choosing a risk metric, an agent is picking an aspect of perceived risk to investigate, such as volatility or probability of default. Risk measure and risk metric In a general sense, a measure is a procedure for quantifying something. A metric is that which is being quantified. In other words, the method or formula to calculate a risk metric is called a risk measure. For example, in finance, the volatility of a stock might be calculated in any one of the three following ways: * Calculate the sample standard deviation of the stock's returns over the past 30 trading days. * Calculate the sample standard deviation of the stock's returns over the past 100 trading days. * Calculate the implied volatility of the stock from some specified call option on the stock. These are three distinct risk measures. Each could be used to measure the single risk metric volatility. Examples * De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk Measure
In financial mathematics, a risk measure is used to determine the amount of an asset or set of assets (traditionally currency) to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator. In recent years attention has turned towards convex and coherent risk measurement. Mathematically A risk measure is defined as a mapping from a set of random variables to the real numbers. This set of random variables represents portfolio returns. The common notation for a risk measure associated with a random variable X is \rho(X). A risk measure \rho: \mathcal \to \mathbb \cup \ should have certain properties: ; Normalized : \rho(0) = 0 ; Translative : \mathrm\; a \in \mathbb \; \mathrm \; Z \in \mathcal ,\;\mathrm\; \rho(Z + a) = \rho(Z) - a ; Monotone : \mathrm\; Z_1,Z_2 \in \mathcal \;\mathrm\; Z_1 \leq Z_2 ,\; \mathrm \; \rho(Z_2) \leq \rho(Z_1) Set-valued In a situation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
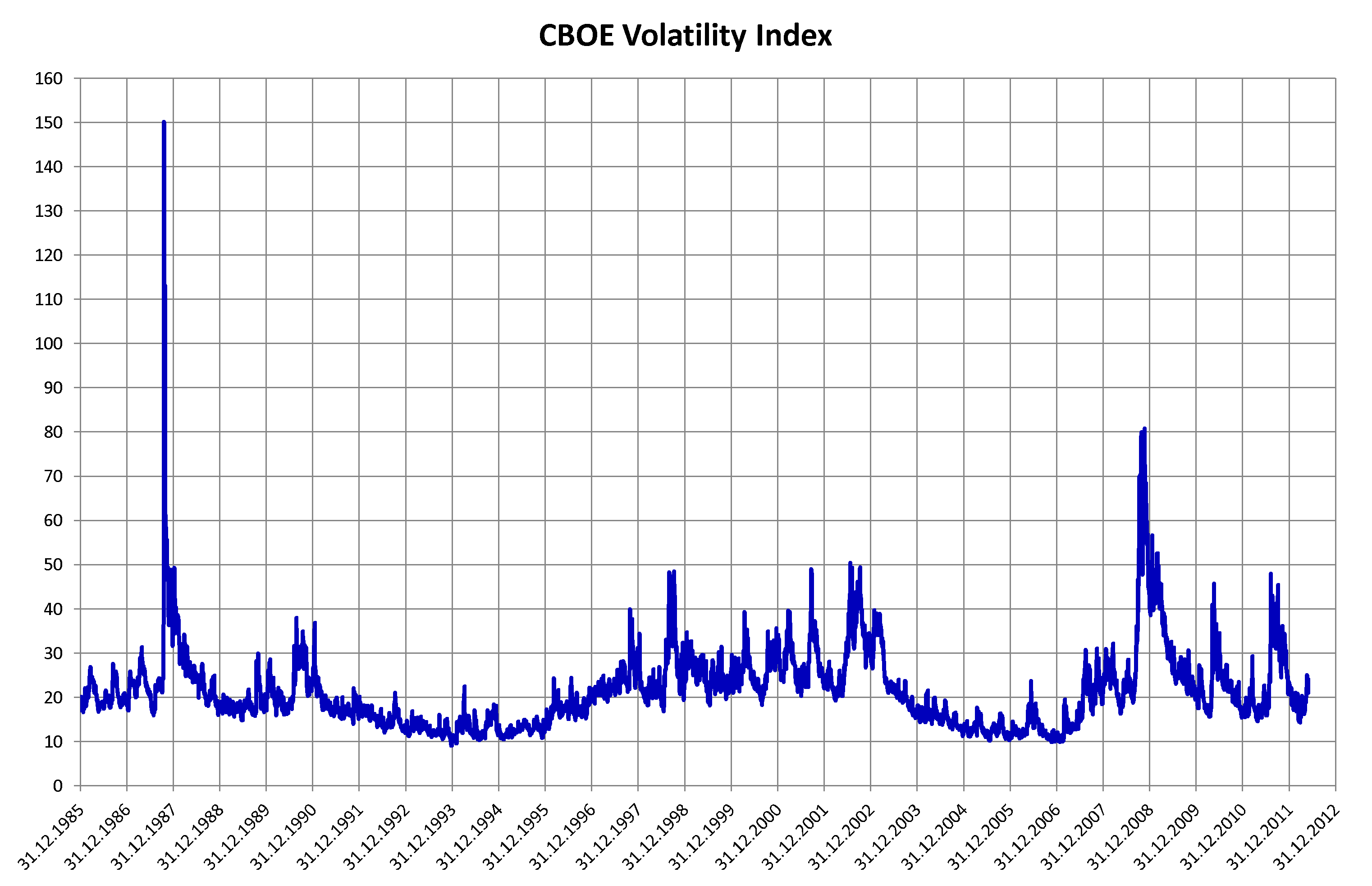
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Value At Risk
Value at risk (VaR) is a measure of the risk of loss for investments. It estimates how much a set of investments might lose (with a given probability), given normal market conditions, in a set time period such as a day. VaR is typically used by firms and regulators in the financial industry to gauge the amount of assets needed to cover possible losses. For a given portfolio, time horizon, and probability ''p'', the ''p'' VaR can be defined informally as the maximum possible loss during that time after excluding all worse outcomes whose combined probability is at most ''p''. This assumes mark-to-market pricing, and no trading in the portfolio. For example, if a portfolio of stocks has a one-day 95% VaR of $1 million, that means that there is a 0.05 probability that the portfolio will fall in value by more than $1 million over a one-day period if there is no trading. Informally, a loss of $1 million or more on this portfolio is expected on 1 day out of 20 days (because of 5% pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk Measure
In financial mathematics, a risk measure is used to determine the amount of an asset or set of assets (traditionally currency) to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator. In recent years attention has turned towards convex and coherent risk measurement. Mathematically A risk measure is defined as a mapping from a set of random variables to the real numbers. This set of random variables represents portfolio returns. The common notation for a risk measure associated with a random variable X is \rho(X). A risk measure \rho: \mathcal \to \mathbb \cup \ should have certain properties: ; Normalized : \rho(0) = 0 ; Translative : \mathrm\; a \in \mathbb \; \mathrm \; Z \in \mathcal ,\;\mathrm\; \rho(Z + a) = \rho(Z) - a ; Monotone : \mathrm\; Z_1,Z_2 \in \mathcal \;\mathrm\; Z_1 \leq Z_2 ,\; \mathrm \; \rho(Z_2) \leq \rho(Z_1) Set-valued In a situation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent Risk Measure
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance. Properties Consider a random outcome X viewed as an element of a linear space \mathcal of measurable functions, defined on an appropriate probability space. A functional \varrho : \mathcal → \R \cup \ is said to be coherent risk measure for \mathcal if it satisfies the following properties: Normalized : \varrho(0) = 0 That is, the risk when holding no assets is zero. Monotonicity : \mathrm\; Z_1,Z_2 \in \mathcal \;\mathrm\; Z_1 \leq Z_2 \; \mathrm ,\; \mathrm \; \varrho(Z_1) \geq \varrho(Z_2) That is, if portfolio Z_2 always has better values than portfolio Z_1 under almost all scenarios then the risk of Z_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deviation Risk Measure
In financial mathematics, a deviation risk measure is a function to quantify financial risk (and not necessarily downside risk) in a different method than a general risk measure. Deviation risk measures generalize the concept of standard deviation. Mathematical definition A function D: \mathcal^2 \to ,+\infty/math>, where \mathcal^2 is the L2 space of random variables (random portfolio returns), is a deviation risk measure if # Shift-invariant: D(X + r) = D(X) for any r \in \mathbb # Normalization: D(0) = 0 # Positively homogeneous: D(\lambda X) = \lambda D(X) for any X \in \mathcal^2 and \lambda > 0 # Sublinearity: D(X + Y) \leq D(X) + D(Y) for any X, Y \in \mathcal^2 # Positivity: D(X) > 0 for all nonconstant ''X'', and D(X) = 0 for any constant ''X''. Relation to risk measure There is a one-to-one relationship between a deviation risk measure ''D'' and an expectation-bounded risk measure ''R'' where for any X \in \mathcal^2 * D(X) = R(X - \mathbb * R(X) = D(X) - \mathbb / ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Risk Measure
A Spectral risk measure is a risk measure given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio returns and outputs the amount of the numeraire (typically a currency) to be kept in reserve. A spectral risk measure is always a coherent risk measure, but the converse does not always hold. An advantage of spectral measures is the way in which they can be related to risk aversion, and particularly to a utility function, through the weights given to the possible portfolio returns. Definition Consider a portfolio X (denoting the portfolio payoff). Then a spectral risk measure M_: \mathcal \to \mathbb where \phi is non-negative, non-increasing, right-continuous, integrable function defined on ,1/math> such that \int_0^1 \phi(p)dp = 1 is defined by :M_(X) = -\int_0^1 \phi(p) F_X^(p) dp where F_X is the cumulative distribution function for ''X''. If there are S equiprobable outcomes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distortion Risk Measure
In financial mathematics and economics, a distortion risk measure is a type of risk measure which is related to the cumulative distribution function of the return of a financial portfolio. Mathematical definition The function \rho_g: L^p \to \mathbb associated with the distortion function g: ,1\to ,1/math> is a ''distortion risk measure'' if for any random variable of gains X \in L^p (where L^p is the Lp space) then : \rho_g(X) = -\int_0^1 F_^(p) d\tilde(p) = \int_^0 \tilde(F_(x))dx - \int_0^ g(1 - F_(x)) dx where F_ is the cumulative distribution function for -X and \tilde is the dual distortion function \tilde(u) = 1 - g(1-u). If X \leq 0 almost surely then \rho_g is given by the Choquet integral, i.e. \rho_g(X) = -\int_0^ g(1 - F_(x)) dx. Equivalently, \rho_g(X) = \mathbb^ X/math> such that \mathbb is the probability measure generated by g, i.e. for any A \in \mathcal the sigma-algebra then \mathbb(A) = g(\mathbb(A)). Properties In addition to the properties of gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |