|
Ringing Artifact
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a bell after being struck. As with other artifacts, their minimization is a criterion in filter design. Introduction The main cause of ringing artifacts is due to a signal being bandlimited (specifically, not having high frequencies) or passed through a low-pass filter; this is the frequency domain description. In terms of the time domain, the cause of this type of ringing is the ripples in the sinc function,, section I.6, Enhancement: Frequency Domain Techniquesp. 16/ref> which is the impulse response (ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ringing Artifact Example
Ringing may mean: Vibrations * Ringing (signal), unwanted oscillation of a signal, leading to ringing artifacts * Vibration of a harmonic oscillator ** Bell ringing * Ringing (telephony), the sound of a telephone bell * Ringing (medicine), a ringing sound in the ears Other uses * Bird ringing, using numbered small metal pr plastic leg rings to track birds * Ringing (of vehicles), the illegal practice of stealing a vehicle and replacing its identification number with that of another vehicle of the same model which has been a write off, write-off See also * Wringing (other) * Ring (other) * {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Phenomenon
In mathematics, the Gibbs phenomenon, discovered by Available on-line at:National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979. and rediscovered by , is the oscillatory behavior of the Fourier series of a piecewise continuously differentiable periodic function around a jump discontinuity. The function's Nth partial Fourier series (formed by summing its N lowest constituent sinusoids) produces large peaks around the jump which overshoot and undershoot the function's actual values. This approximation error approaches a limit of about 9% of the jump as more sinusoids are used, though the infinite Fourier series sum does eventually converge almost everywhere except the point of discontinuity. The Gibbs phenomenon was observed by experimental physicists, but was believed to be due to imperfections in the measuring apparatus, and it is one cause of ringing artifacts in signal processing. Description The Gibbs phenomenon involves both the fact that Fourier su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Integral
In mathematics, trigonometric integrals are a indexed family, family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth Bessel function#Spherical Bessel functions: jn.2C yn, spherical Bessel function. Since is an even function, even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along Cauchy's integral theorem, any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Filter
In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given cutoff frequency, without affecting lower frequencies, and has linear phase response. The filter's impulse response is a sinc function in the time domain and its frequency response is a rectangular function. It is an "ideal" low-pass filter in the frequency sense, perfectly passing low frequencies, perfectly cutting high frequencies; and thus may be considered to be a ''brick-wall filter''. Real-time filters can only approximate this ideal, since an ideal sinc filter (a.k.a. ''rectangular filter'') is non-causal and has an infinite delay, but it is commonly found in conceptual demonstrations or proofs, such as the sampling theorem and the Whittaker–Shannon interpolation formula. In mathematical terms, the desired frequency response is the rectangular function: :H(f) = \operatorname \left( \frac \right) = \begin 0, & \text , f, > B, \\ \frac, & \text , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brick-wall Filter
In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given cutoff frequency, without affecting lower frequencies, and has linear phase response. The filter's impulse response is a sinc function in the time domain and its frequency response is a rectangular function. It is an "ideal" low-pass filter in the frequency sense, perfectly passing low frequencies, perfectly cutting high frequencies; and thus may be considered to be a ''brick-wall filter''. Real-time filters can only approximate this ideal, since an ideal sinc filter (a.k.a. ''rectangular filter'') is non-causal and has an infinite delay, but it is commonly found in conceptual demonstrations or proofs, such as the sampling theorem and the Whittaker–Shannon interpolation formula. In mathematical terms, the desired frequency response is the rectangular function: :H(f) = \operatorname \left( \frac \right) = \begin 0, & \text , f, > B, \\ \frac, & \text , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Integral
In mathematics, trigonometric integrals are a indexed family, family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth Bessel function#Spherical Bessel functions: jn.2C yn, spherical Bessel function. Since is an even function, even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along Cauchy's integral theorem, any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time Invariant
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined below. These properties apply (exactly or approximately) to many important physical systems, in which case the response of the system to an arbitrary input can be found directly using convolution: where is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication, as is frequently employed by the symbol in computer languages). What's more, there are systematic methods for solving any such system (determining ), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers. Linear time-invariant system theory i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter (signal Processing)
In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other targets for filtering exist. Correlations can be removed for certain frequency components and not for others without having to act in the frequency domain. Filters are widely used in electronics and telecommunication, in radio, television, audio recording, radar, control systems, music synthesis, image processing, and computer graphics. There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Filters may be: *non-linear or linear *time-variant or t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
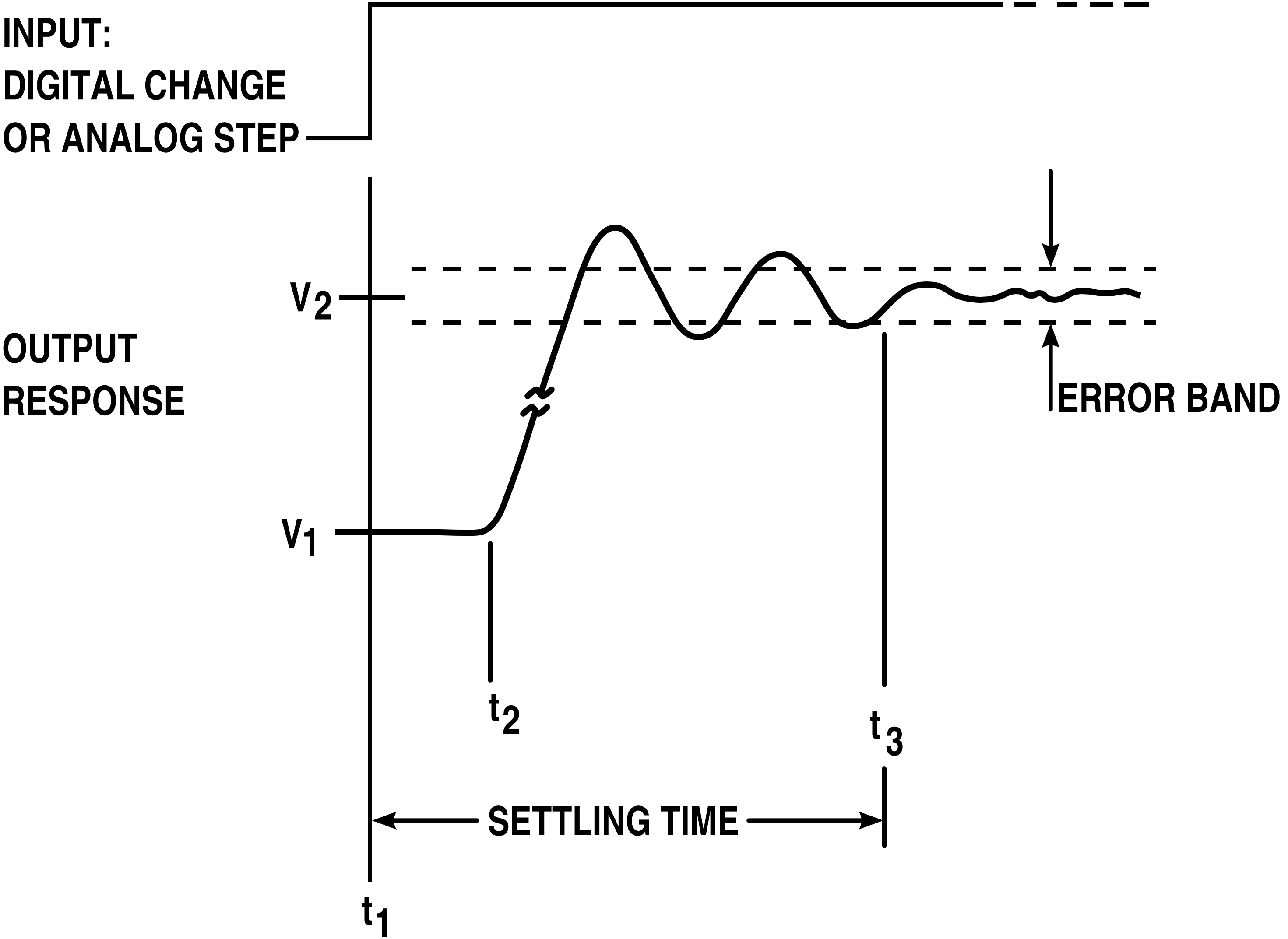
Step Response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from zero to one in a very short time. The concept can be extended to the abstract mathematical notion of a dynamical system using an evolution parameter. From a practical standpoint, knowing how the system responds to a sudden input is important because large and possibly fast deviations from the long term steady state may have extreme effects on the component itself and on other portions of the overall system dependent on this component. In addition, the overall system cannot act until the component's output settles down to some vicinity of its final state, delaying the overall system response. Formally, knowing the step response of a dynamical system gives information on the stability of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonic Function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if and only if it is either entirely non-increasing, or entirely non-decreasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is called ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Phenomenon 10
Gibbs or GIBBS is a surname and acronym. It may refer to: People * Gibbs (surname) Places * Gibbs (crater), on the Moon * Gibbs, Missouri, US * Gibbs, Tennessee, US * Gibbs Island (South Shetland Islands), Antarctica * 2937 Gibbs, an asteroid Science Mathematics and statistics * Gibbs phenomenon * Gibbs' inequality * Gibbs sampling Physics * Gibbs phase rule * Gibbs free energy * Gibbs entropy * Gibbs paradox * Gibbs–Helmholtz equation * Gibbs algorithm * Gibbs state * Gibbs-Marangoni effect * Gibbs phenomenon, an MRI artifact Organisations * Gibbs & Cox naval architecture firm * Gothenburg International Bioscience Business School * Gibbs College, several US locations * Gibbs Technologies, developer and manufacturer of amphibious vehicles * Gibbs High School (other), several schools of this name exist * Antony Gibbs & Sons, British trading company, established in London in 1802 Other uses * Gibbs SR, former name of the toothpaste Mentadent * Gibbs Stadium, Spar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Gibbs Phenomenon")
.svg "Click for more on -> Sinc Filter")
