|
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term (logic)
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact. A first-order term is recursively constructed from constant symbols, variable symbols, and function symbols. An expression formed by applying a predicate symbol to an appropriate number of terms is called an atomic formula, which evaluates to true or false in bivalent logics, given an interpretation. For example, is a term built from the constant 1, the variable , and the binary function symbols and ; it is part of the atomic formula which evaluates to true for each real-numbered value of . Besides in logic, terms play important roles in universal algebra, and rewriting systems. Definition Given a set ''V'' of variable symbols, a set ''C'' of constant symbols and sets ''F''''n'' of ''n''-ary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs (x, y), where x is an element of X and y is an element of Y. It encodes the common concept of relation: an element x is ''related'' to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime p is related to each integer z that is a Divisibility, multiple of p, but not to an integer that is not a Multiple (mathematics), multiple of p. In this relation, for instance, the prime number 2 is related to numbers such as -4, 0, 6, 10, but not to 1 or 9, just as the prime number 3 is related to 0, 6, and 9, but not to 4 or 13. Binary relations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generative Grammar
Generative grammar is a research tradition in linguistics that aims to explain the cognitive basis of language by formulating and testing explicit models of humans' subconscious grammatical knowledge. Generative linguists, or generativists (), tend to share certain working assumptions such as the competence–performance distinction and the notion that some domain-specific aspects of grammar are partly innate in humans. These assumptions are rejected in non-generative approaches such as usage-based models of language. Generative linguistics includes work in core areas such as syntax, semantics, phonology, psycholinguistics, and language acquisition, with additional extensions to topics including biolinguistics and music cognition. Generative grammar began in the late 1950s with the work of Noam Chomsky, having roots in earlier approaches such as structural linguistics. The earliest version of Chomsky's model was called Transformational grammar, with subsequent itera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
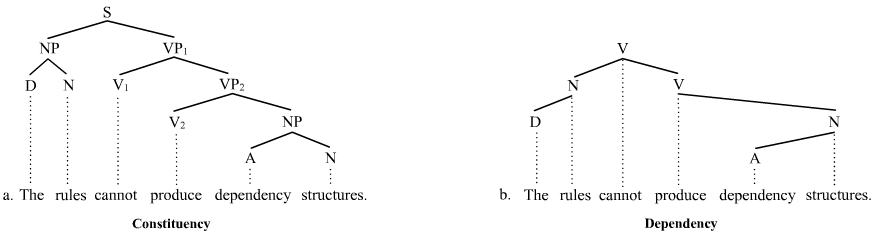
Phrase Structure Rule
Phrase structure rules are a type of rewrite rule used to describe a given language's syntax and are closely associated with the early stages of transformational grammar, proposed by Noam Chomsky in 1957. They are used to break down a natural language sentence into its constituent parts, also known as syntactic category, syntactic categories, including both lexical categories (part of speech, parts of speech) and phrase, phrasal categories. A grammar that uses phrase structure rules is a type of phrase structure grammar. Phrase structure rules as they are commonly employed operate according to the constituent (linguistics), constituency relation, and a grammar that employs phrase structure rules is therefore a phrase structure grammar, ''constituency grammar''; as such, it stands in contrast to dependency grammar, ''dependency grammars'', which are based on the government (linguistics), dependency relation. Definition and examples Phrase structure rules are usually of the following ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automated Theorem Proving
Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major motivating factor for the development of computer science. Logical foundations While the roots of formalized Logicism, logic go back to Aristotelian logic, Aristotle, the end of the 19th and early 20th centuries saw the development of modern logic and formalized mathematics. Gottlob Frege, Frege's ''Begriffsschrift'' (1879) introduced both a complete propositional logic, propositional calculus and what is essentially modern predicate logic. His ''The Foundations of Arithmetic, Foundations of Arithmetic'', published in 1884, expressed (parts of) mathematics in formal logic. This approach was continued by Bertrand Russell, Russell and Alfred North Whitehead, Whitehead in their influential ''Principia Mathematica'', first published 1910� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Equivalence
In logic and mathematics, statements p and q are said to be logically equivalent if they have the same truth value in every model. The logical equivalence of p and q is sometimes expressed as p \equiv q, p :: q, \textsfpq, or p \iff q, depending on the notation being used. However, these symbols are also used for material equivalence, so proper interpretation would depend on the context. Logical equivalence is different from material equivalence, although the two concepts are intrinsically related. Logical equivalences In logic, many common logical equivalences exist and are often listed as laws or properties. The following tables illustrate some of these. General logical equivalences Logical equivalences involving conditional statements :#p \rightarrow q \equiv \neg p \vee q :#p \rightarrow q \equiv \neg q \rightarrow \neg p :#p \vee q \equiv \neg p \rightarrow q :#p \wedge q \equiv \neg (p \rightarrow \neg q) :#\neg (p \rightarrow q) \equiv p \wedge \neg q :#(p \righta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Verb Phrase
In linguistics, a verb phrase (VP) is a syntax, syntactic unit composed of a verb and its argument (linguistics), arguments except the subject (grammar), subject of an independent clause or coordinate clause. Thus, in the sentence ''A fat man quickly put the money into the box'', the words ''quickly put the money into the box'' constitute a verb phrase; it consists of the verb ''put'' and its arguments, but not the subject ''a fat man''. A verb phrase is similar to what is considered a ''predicate (grammar), predicate'' in traditional grammars. Verb phrases generally are divided among two types: finite, of which the Head (linguistics), head of the phrase is a finite verb; and nonfinite, where the head is a nonfinite verb, such as an infinitive, participle or gerund. Phrase structure grammars acknowledge both types, but dependency grammars treat the subject as just another verbal dependent, and they do not recognize the finite verbal phrase constituent (linguistics), constituent. Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morpheme
A morpheme is any of the smallest meaningful constituents within a linguistic expression and particularly within a word. Many words are themselves standalone morphemes, while other words contain multiple morphemes; in linguistic terminology, this is the distinction, respectively, between free and bound morphemes. The field of linguistic study dedicated to morphemes is called morphology. In English, inside a word with multiple morphemes, the main morpheme that gives the word its basic meaning is called a root (such as ''cat'' inside the word ''cats''), which can be bound or free. Meanwhile, additional bound morphemes, called affixes, may be added before or after the root, like the ''-s'' in ''cats'', which indicates plurality but is always bound to a root noun and is not regarded as a word on its own. However, in some languages, including English and Latin Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European langua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sentence (linguistics)
In linguistics and grammar, a sentence is a Expression (linguistics), linguistic expression, such as the English example "The quick brown fox jumps over the lazy dog." In traditional grammar, it is typically defined as a string of words that expresses a complete thought, or as a unit consisting of a Subject (grammar), subject and Predicate (grammar), predicate. In non-functional linguistics it is typically defined as a maximal unit of syntactic structure such as a Constituent_(linguistics), constituent. In functional linguistics, it is defined as a unit of written texts delimited by writing, graphological features such as upper-case letters and markers such as periods, question marks, and exclamation marks. This notion contrasts with a curve, which is delimited by phonologic features such as pitch and loudness and markers such as pauses; and with a clause, which is a sequence of words that represents some process going on throughout time. A sentence can include words grouped meaning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noun Phrase
A noun phrase – or NP or nominal (phrase) – is a phrase that usually has a noun or pronoun as its head, and has the same grammatical functions as a noun. Noun phrases are very common cross-linguistically, and they may be the most frequently occurring phrase type. Noun phrases often function as verb subjects and objects, as predicative expressions, and as complements of prepositions. One NP can be embedded inside another NP; for instance, ''some of his constituents'' has as a constituent the shorter NP ''his constituents''. In some theories of grammar, noun phrases with determiners are analyzed as having the determiner as the head of the phrase, see for instance Chomsky (1995) and Hudson (1990) . Identification Some examples of noun phrases are underlined in the sentences below. The head noun appears in bold. ::This election-year's politics are annoying for many people. ::Almost every sentence contains at least one noun phrase. ::Current economic weakness may be a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntactic Category
A syntactic category is a syntactic unit that theories of syntax assume. Word classes, largely corresponding to traditional parts of speech (e.g. noun, verb, preposition, etc.), are syntactic categories. In phrase structure grammars, the ''phrasal categories'' (e.g. noun phrase, verb phrase, prepositional phrase, etc.) are also syntactic categories. Dependency grammars, however, do not acknowledge phrasal categories (at least not in the traditional sense). Word classes considered as syntactic categories may be called ''lexical categories'', as distinct from phrasal categories. The terminology is somewhat inconsistent between the theoretical models of different linguists. However, many grammars also draw a distinction between ''lexical categories'' (which tend to consist of content words, or phrases headed by them) and ''functional categories'' (which tend to consist of function words or abstract functional elements, or phrases headed by them). The term ''lexical category'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linguistics
Linguistics is the scientific study of language. The areas of linguistic analysis are syntax (rules governing the structure of sentences), semantics (meaning), Morphology (linguistics), morphology (structure of words), phonetics (speech sounds and equivalent gestures in sign languages), phonology (the abstract sound system of a particular language, and analogous systems of sign languages), and pragmatics (how the context of use contributes to meaning). Subdisciplines such as biolinguistics (the study of the biological variables and evolution of language) and psycholinguistics (the study of psychological factors in human language) bridge many of these divisions. Linguistics encompasses Outline of linguistics, many branches and subfields that span both theoretical and practical applications. Theoretical linguistics is concerned with understanding the universal grammar, universal and Philosophy of language#Nature of language, fundamental nature of language and developing a general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |