|
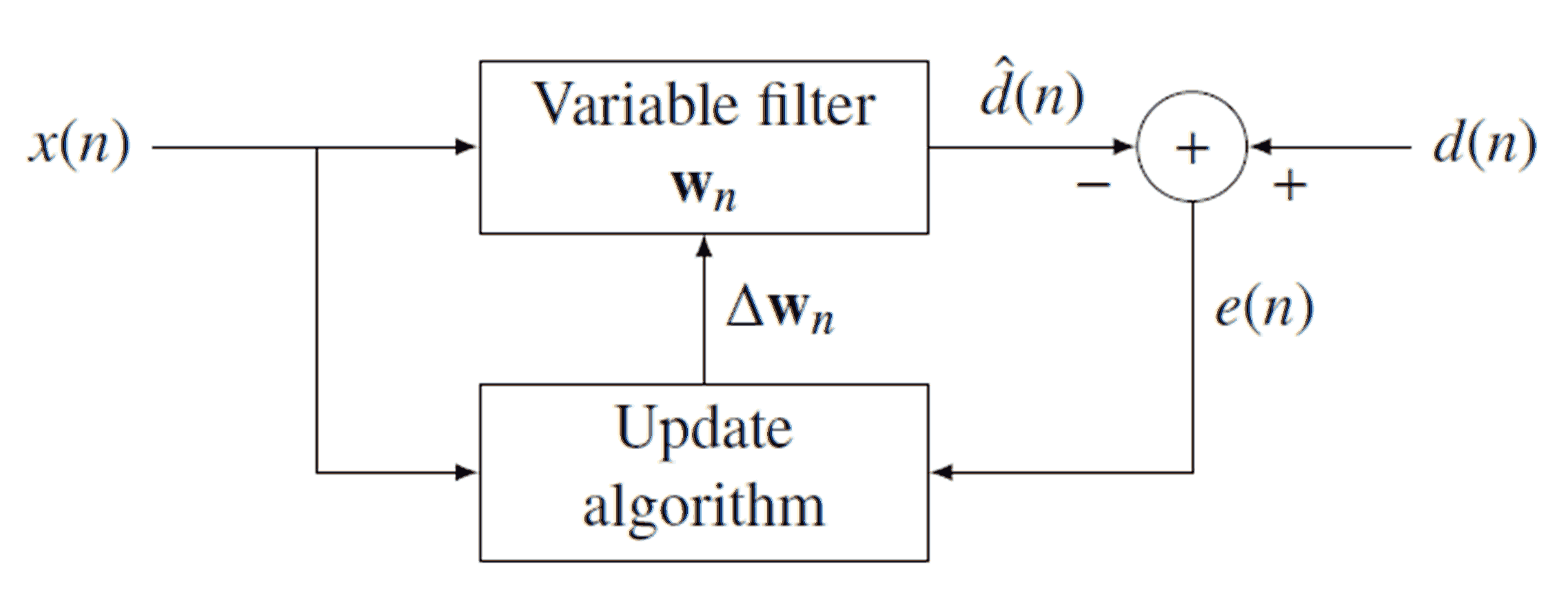
Recursive Least Squares
Recursive least squares (RLS) is an adaptive filter algorithm that recursively finds the coefficients that minimize a Weighted least squares, weighted linear least squares Loss function, cost function relating to the input signals. This approach is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic system (mathematics), deterministic, while for the LMS and similar algorithms they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity. Motivation RLS was discovered by Carl Friedrich Gauss, Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kalman Filter
In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unknown variables that tend to be more accurate than those based on a single measurement, by estimating a joint probability distribution over the variables for each time-step. The filter is constructed as a mean squared error minimiser, but an alternative derivation of the filter is also provided showing how the filter relates to maximum likelihood statistics. The filter is named after Rudolf E. Kálmán. Kalman filtering has numerous technological applications. A common application is for guidance, navigation, and control of vehicles, particularly aircraft, spacecraft and ships Dynamic positioning, positioned dynamically. Furthermore, Kalman filtering is much applied in time series analysis tasks such as signal processing and econometrics. K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-forcing Equalizer
The zero-forcing equalizer is a form of linear equalization algorithm used in communication systems which applies the inverse of the frequency response of the channel. This form of equalizer was first proposed by Robert Lucky. The zero-forcing equalizer applies the inverse of the channel frequency response to the received signal, to restore the signal after the channel. It has many useful applications. For example, it is studied heavily for IEEE 802.11n (MIMO) where knowing the channel allows recovery of the two or more streams which will be received on top of each other on each antenna. The name ''zero-forcing corresponds'' to bringing down the intersymbol interference (ISI) to zero in a noise-free case. This will be useful when ISI is significant compared to noise. For a channel with frequency response F(f) the zero-forcing equalizer C(f) is constructed by C(f) = 1/F(f). Thus the combination of channel and equalizer gives a flat frequency response and linear phase F(f)C(f) = 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Mean Squares Filter
Least mean squares (LMS) algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean square of the error signal (difference between the desired and the actual signal). It is a stochastic gradient descent method in that the filter is only adapted based on the error at the current time. It was invented in 1960 by Stanford University professor Bernard Widrow and his first Ph.D. student, Ted Hoff, based on their research in single-layer neural networks ( ADALINE). Specifically, they used gradient descent to train ADALINE to recognize patterns, and called the algorithm "delta rule". They then applied the rule to filters, resulting in the LMS algorithm. Problem formulation The picture shows the various parts of the filter. x is the input signal, which is then transformed by an unknown filter h that we wish to match using \hat h. The output from the unknown filter is y, which is then interfered wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Adaptive Filter
In signal processing, a kernel adaptive filter is a type of nonlinear adaptive filter. An adaptive filter is a filter that adapts its transfer function to changes in signal properties over time by minimizing an error or loss function that characterizes how far the filter deviates from ideal behavior. The adaptation process is based on learning from a sequence of signal samples and is thus an online algorithm. A nonlinear adaptive filter is one in which the transfer function is nonlinear. Kernel adaptive filters implement a nonlinear transfer function using kernel methods. In these methods, the signal is mapped to a high-dimensional linear feature space and a nonlinear function is approximated as a sum over kernels, whose domain is the feature space. If this is done in a reproducing kernel Hilbert space, a kernel method can be a universal approximator for a nonlinear function. Kernel methods have the advantage of having convex loss functions, with no local minima, and of being only m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Riccati Equation
An algebraic Riccati equation is a type of nonlinear equation that arises in the context of infinite-horizon optimal control problems in continuous time or discrete time. A typical algebraic Riccati equation is similar to one of the following: the continuous time algebraic Riccati equation (CARE): A^\top P + P A - P B R^ B^\top P + Q = 0 or the discrete time algebraic Riccati equation (DARE): P = A^\top P A -(A^\top P B)(R + B^\top P B)^(B^\top P A) + Q. is the unknown by symmetric matrix and are known real coefficient matrices, with and symmetric. Though generally this equation can have many solutions, it is usually specified that we want to obtain the unique stabilizing solution, if such a solution exists. Origin of the name The name Riccati is given to these equations because of their relation to the Riccati differential equation. Indeed, the CARE is verified by the time invariant solutions of the associated matrix valued Riccati differential equation. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Posteriori
('from the earlier') and ('from the later') are Latin phrases used in philosophy to distinguish types of knowledge, justification, or argument by their reliance on experience. knowledge is independent from any experience. Examples include mathematics,Some associationist philosophers have contended that mathematics comes from experience and is not a form of any ''a priori'' knowledge () tautologies and deduction from pure reason. Galen Strawson has stated that an argument is one in which "you can see that it is true just lying on your couch. You don't have to get up off your couch and go outside and examine the way things are in the physical world. You don't have to do any science." () knowledge depends on empirical evidence. Examples include most fields of science and aspects of personal knowledge. The terms originate from the analytic methods found in '' Organon'', a collection of works by Aristotle. Prior analytics () is about deductive logic, which comes from d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the object remains unchanged by the transformation. In other contexts, it is analogous to multiplying by the number 1. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Woodbury Matrix Identity
In mathematics, specifically linear algebra, the Woodbury matrix identity – named after Max A. Woodbury – says that the inverse of a rank-''k'' correction of some matrix can be computed by doing a rank-''k'' correction to the inverse of the original matrix. Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the Woodbury report. The Woodbury matrix identity is \left(A + UCV \right)^ = A^ - A^U \left(C^ + VA^U \right)^ VA^, where ''A'', ''U'', ''C'' and ''V'' are conformable matrices: ''A'' is ''n''×''n'', ''C'' is ''k''×''k'', ''U'' is ''n''×''k'', and ''V'' is ''k''×''n''. This can be derived using blockwise matrix inversion. While the identity is primarily used on matrices, it holds in a general ring or in an Ab-category. The Woodbury matrix identity allows cheap computation of inverses and solutions to linear equations. However ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross-covariance
In probability and statistics, given two stochastic processes \left\ and \left\, the cross-covariance is a function that gives the covariance of one process with the other at pairs of time points. With the usual notation \operatorname E for the expectation operator, if the processes have the mean functions \mu_X(t) = \operatorname \operatorname E _t/math> and \mu_Y(t) = \operatorname E _t/math>, then the cross-covariance is given by :\operatorname_(t_1,t_2) = \operatorname (X_, Y_) = \operatorname X_ - \mu_X(t_1))(Y_ - \mu_Y(t_2))= \operatorname _ Y_- \mu_X(t_1) \mu_Y(t_2).\, Cross-covariance is related to the more commonly used cross-correlation of the processes in question. In the case of two random vectors \mathbf=(X_1, X_2, \ldots , X_p)^ and \mathbf=(Y_1, Y_2, \ldots , Y_q)^, the cross-covariance would be a p \times q matrix \operatorname_ (often denoted \operatorname(X,Y)) with entries \operatorname_(j,k) = \operatorname(X_j, Y_k).\, Thus the term ''cross-covariance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |