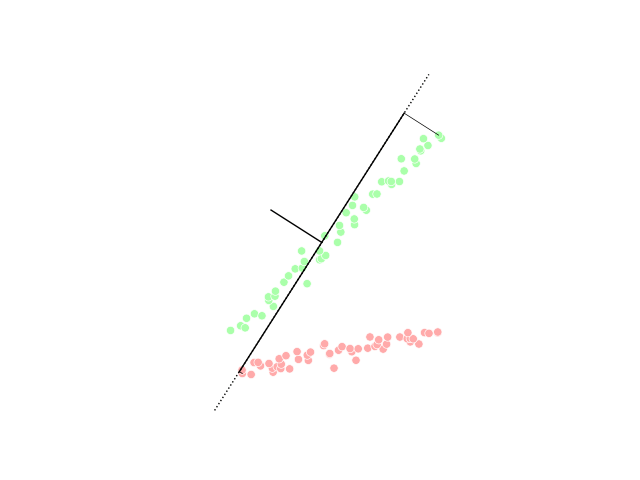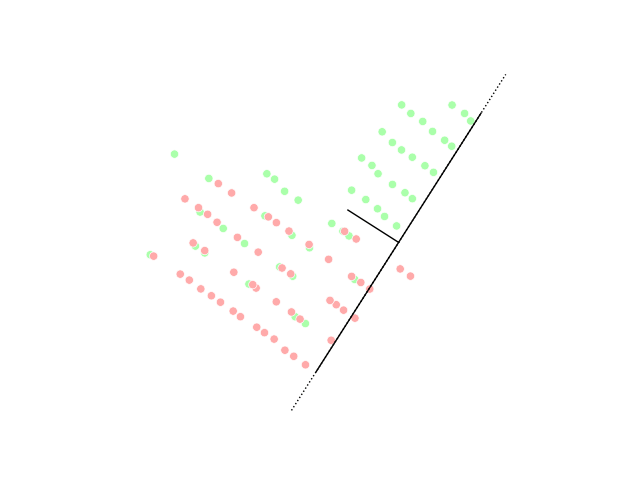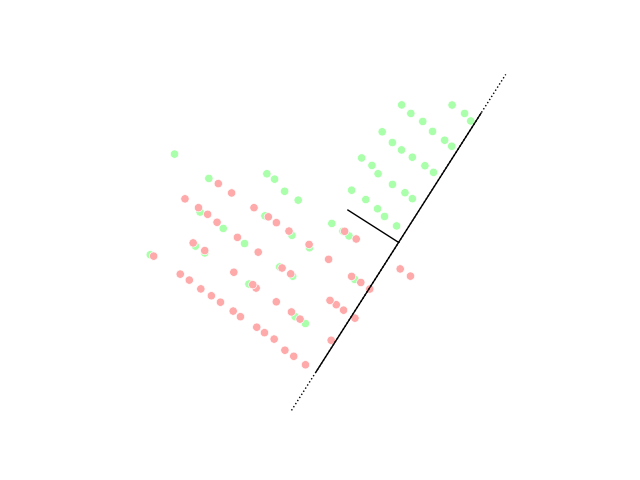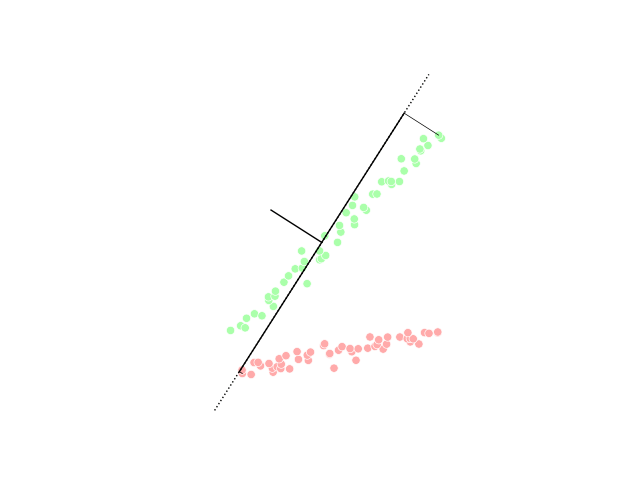
|
Random Projection
In mathematics and statistics, random projection is a technique used to reduce the dimensionality of a set of points which lie in Euclidean space. Random projection methods are known for their power, simplicity, and low error rates when compared to other methods. According to experimental results, random projection preserves distances well, but empirical results are sparse. They have been applied to many natural language tasks under the name random indexing. Dimensionality reduction Dimensionality reduction, as the name suggests, is reducing the number of random variables using various mathematical methods from statistics and machine learning. Dimensionality reduction is often used to reduce the problem of managing and manipulating large data sets. Dimensionality reduction techniques generally use linear transformations in determining the intrinsic dimensionality of the manifold as well as extracting its principal directions. For this purpose there are various related techniques, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson–Lindenstrauss Lemma
In mathematics, the Johnson–Lindenstrauss lemma is a result named after William B. Johnson and Joram Lindenstrauss concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. The map used for the embedding is at least Lipschitz, and can even be taken to be an orthogonal projection. The lemma has applications in compressed sensing, manifold learning, dimensionality reduction, and graph embedding. Much of the data stored and manipulated on computers, including text and images, can be represented as points in a high-dimensional space (see vector space model for the case of text). However, the essential algorithms for working with such data tend to become bogged down very quickly as dimension increases. It is therefore desirable to reduce the dimensio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locality-sensitive Hashing
In computer science, locality-sensitive hashing (LSH) is an algorithmic technique that hashes similar input items into the same "buckets" with high probability. (The number of buckets is much smaller than the universe of possible input items.) Since similar items end up in the same buckets, this technique can be used for data clustering and nearest neighbor search. It differs from conventional hashing techniques in that hash collisions are maximized, not minimized. Alternatively, the technique can be seen as a way to reduce the dimensionality of high-dimensional data; high-dimensional input items can be reduced to low-dimensional versions while preserving relative distances between items. Hashing-based approximate nearest neighbor search algorithms generally use one of two main categories of hashing methods: either data-independent methods, such as locality-sensitive hashing (LSH); or data-dependent methods, such as locality-preserving hashing (LPH). Definitions An ''LSH family'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scikit-learn
scikit-learn (formerly scikits.learn and also known as sklearn) is a free software machine learning library for the Python programming language. It features various classification, regression and clustering algorithms including support-vector machines, random forests, gradient boosting, ''k''-means and DBSCAN, and is designed to interoperate with the Python numerical and scientific libraries NumPy and SciPy. Scikit-learn is a NumFOCUS fiscally sponsored project. Overview The scikit-learn project started as scikits.learn, a Google Summer of Code project by French data scientist David Cournapeau. The name of the project stems from the notion that it is a "SciKit" (SciPy Toolkit), a separately developed and distributed third-party extension to SciPy. The original codebase was later rewritten by other developers. In 2010, contributors Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort and Vincent Michel, from the French Institute for Research in Computer Science and Auto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Sciences (journal)
''Information Sciences'' is a bimonthly peer-reviewed academic journal covering information science. It was established in 1968 and is published by Elsevier. The editor-in-chief is Witold Pedrycz (University of Alberta). According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 8.233. References External links * Elsevier academic journals Publications established in 1968 Bimonthly journals Information science journals English-language journals {{Scientific-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making predicti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Database Index
A database index is a data structure that improves the speed of data retrieval operations on a database table at the cost of additional writes and storage space to maintain the index data structure. Indexes are used to quickly locate data without having to search every row in a database table every time a database table is accessed. Indexes can be created using one or more columns of a database table, providing the basis for both rapid random lookups and efficient access of ordered records. An index is a copy of selected columns of data, from a table, that is designed to enable very efficient search. An index normally includes a "key" or direct link to the original row of data from which it was copied, to allow the complete row to be retrieved efficiently. Some databases extend the power of indexing by letting developers create indexes on column values that have been transformed by functions or expressions. For example, an index could be created on upper(last_name), which wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inner Product Space
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in \langle a, b \rangle. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality (zero inner product) of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or ''scalar product'' of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898. An inner product naturally induces an associated norm, (denoted , x, and , y, in the picture) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics * In optics, polarization states are said to be orthogonal when they propagate independently of each other, as in vertical and horizontal linear polarization or right- and left-handed circular polarization. * In special relativity, a time axis determined by a rapidity of motion is hyperbolic-orthogonal to a space axis o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis (linear Algebra)
In mathematics, a set of vectors in a vector space is called a basis if every element of may be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the ''dimension'' of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Definition A basis of a vector space over a field (such as the real numbers or the complex numbers ) is a linearly independent subset of that spans . Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the '' Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The ACM
The ''Journal of the ACM'' is a peer-reviewed scientific journal covering computer science in general, especially theoretical aspects. It is an official journal of the Association for Computing Machinery. Its current editor-in-chief is Venkatesan Guruswami. The journal was established in 1954 and "computer scientists universally hold the ''Journal of the ACM'' in high esteem". See also * ''Communications of the ACM ''Communications of the ACM'' is the monthly journal of the Association for Computing Machinery (ACM). It was established in 1958, with Saul Rosen as its first managing editor. It is sent to all ACM members. Articles are intended for readers wi ...'' References External links * Publications established in 1954 Computer science journals Association for Computing Machinery academic journals Bimonthly journals English-language journals {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
