|
Quantum-confined Stark Effect
The quantum-confined Stark effect (QCSE) describes the effect of an external electric field upon the light absorption spectrum or emission spectrum of a quantum well (QW). In the absence of an external electric field, electrons and holes within the quantum well may only occupy states within a discrete set of energy subbands. Only a discrete set of frequencies of light may be absorbed or emitted by the system. When an external electric field is applied, the electron states shift to lower energies, while the hole states shift to higher energies. This reduces the permitted light absorption or emission frequencies. Additionally, the external electric field shifts electrons and holes to opposite sides of the well, decreasing the overlap integral, which in turn reduces the recombination efficiency (i.e. fluorescence quantum yield) of the system. The spatial separation between the electrons and holes is limited by the presence of the potential barriers around the quantum well, mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stark Effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to the presence of an external electric field. It is the electric-field analogue of the Zeeman effect, where a spectral line is split into several components due to the presence of the magnetic field. Although initially coined for the static case, it is also used in the wider context to describe the effect of time-dependent electric fields. In particular, the Stark effect is responsible for the pressure broadening (Stark broadening) of spectral lines by charged particles in plasmas. For most spectral lines, the Stark effect is either linear (proportional to the applied electric field) or quadratic with a high accuracy. The Stark effect can be observed both for emission and absorption lines. The latter is sometimes called the inverse Stark effect, but this term is no longer used in the modern literature. History The effect is named after the German physicist Johannes Stark, who discov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Mass (solid-state Physics)
In solid state physics, a particle's effective mass (often denoted m^*) is the mass that it ''seems'' to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors. For electrons or electron holes in a solid, the effective mass is usually stated as a factor multiplying the rest mass of an electron, ''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
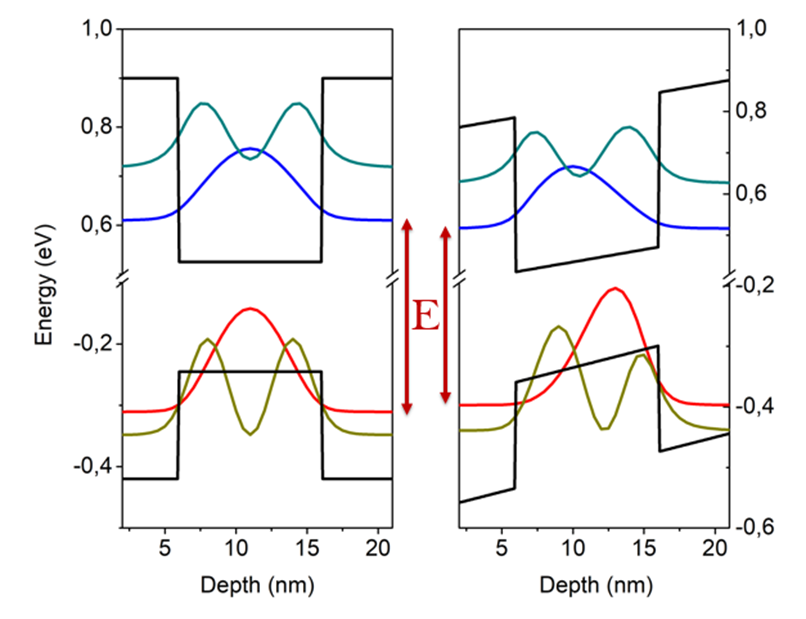
QCSE GaAs-AlGaAs QW
The quantum-confined Stark effect (QCSE) describes the effect of an external electric field upon the light absorption spectrum or emission spectrum of a quantum well (QW). In the absence of an external electric field, electrons and holes within the quantum well may only occupy states within a discrete set of energy subbands. Only a discrete set of frequencies of light may be absorbed or emitted by the system. When an external electric field is applied, the electron states shift to lower energies, while the hole states shift to higher energies. This reduces the permitted light absorption or emission frequencies. Additionally, the external electric field shifts electrons and holes to opposite sides of the well, decreasing the overlap integral, which in turn reduces the recombination efficiency (i.e. fluorescence quantum yield) of the system. The spatial separation between the electrons and holes is limited by the presence of the potential barriers around the quantum well, meanin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in an electric field. More precisely, it is the energy per unit charge for a test charge that is so small that the disturbance of the field under consideration is negligible. Furthermore, the motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar quantity denoted by or occasionally , equal to the electric potential energy o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bohr Radius
The Bohr radius (''a''0) is a physical constant, approximately equal to the most probable distance between the nucleus and the electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom. Its value is The number in parenthesis denotes the uncertainty of the last digits. Definition and value The Bohr radius is defined as a_0 = \frac = \frac = \frac , where * \varepsilon_0 is the permittivity of free space, * \hbar is the reduced Planck constant, * m_ is the mass of an electron, * e is the elementary charge, * c is the speed of light in vacuum, and * \alpha is the fine-structure constant. The CODATA value of the Bohr radius (in SI units) is History In the Bohr model for atomic structure, put forward by Niels Bohr in 1913, electrons orbit a central nucleus under electrostatic attraction. The original derivation posited that electrons have orbital angular momentum in integer multiples of the reduced Planck co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Franz–Keldysh Effect
The Franz–Keldysh effect is a change in optical absorption by a semiconductor when an electric field is applied. The effect is named after the German physicist Walter Franz and Russian physicist Leonid Keldysh. Karl W. Böer observed first the shift of the optical absorption edge with electric fields during the discovery of high-field domains and named this the Franz-effect. A few months later, when the English translation of the Keldysh paper became available, he corrected this to the Franz–Keldysh effect. As originally conceived, the Franz–Keldysh effect is the result of wavefunctions "leaking" into the band gap. When an electric field is applied, the electron and electron hole, hole wavefunctions become Airy functions rather than plane waves. The Airy function includes a "tail" which extends into the classically forbidden band gap. According to Fermi's Golden Rule, Fermi's golden rule, the more overlap there is between the wavefunctions of a free electron and a hole, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Mass
In physics, the reduced mass is the "effective" Mass#Inertial mass, inertial mass appearing in the two-body problem of Newtonian mechanics. It is a quantity which allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass determining the gravitational force is ''not'' reduced. In the computation, one mass ''can'' be replaced with the reduced mass, if this is compensated by replacing the other mass with the sum of both masses. The reduced mass is frequently denoted by \mu (Mu (letter), mu), although the standard gravitational parameter is also denoted by \mu (as are Mu (letter)#Physics and engineering, a number of other physical quantities). It has the dimensional analysis, dimensions of mass, and SI unit kg. Equation Given two bodies, one with mass ''m''1 and the other with mass ''m''2, the equivalent one-body problem, with the position of one body with respect to the other as the unknown, is that of a single body of mass :\mu = \c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rydberg Constant
In spectroscopy, the Rydberg constant, symbol R_\infty for heavy atoms or R_\text for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants via his Bohr model. Before the redefinition of the SI base units in , R_\infty and the electron spin ''g''-factor were the most accurately measured physical constants. The constant is expressed for either hydrogen as R_\text, or at the limit of infinite nuclear mass as R_\infty. In either case, the constant is used to express the limiting value of the highest wavenumber (inverse wavelength) of any photon that can be emitted from an atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing an atom from its ground state. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogenic
A hydrogen-like atom (or hydrogenic atom) is any atom or ion with a single valence electron. These atoms are isoelectronic with hydrogen. Examples of hydrogen-like atoms include, but are not limited to, hydrogen itself, all alkali metals such as Rb and Cs, singly ionized alkaline earth metals such as Ca+ and Sr+ and other ions such as He+, Li2+, and Be3+ and isotopes of any of the above. A hydrogen-like atom includes a positively charged core consisting of the atomic nucleus and any core electrons as well as a single valence electron. Because helium is common in the universe, the spectroscopy of singly ionized helium is important in EUV astronomy, for example, of DO white dwarf stars. The non-relativistic Schrödinger equation and relativistic Dirac equation for the hydrogen atom can be solved analytically, owing to the simplicity of the two-particle physical system. The one-electron wave function solutions are referred to as ''hydrogen-like atomic orbitals''. Hydrogen-li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi's Golden Rule
In quantum physics, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the matrix element of the perturbation) as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth. General Although the rule is named after Enrico Fermi, most of the work leading to it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory (quantum Mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system (e.g. its energy levels and eigenstates) can be expressed as "corrections" to those of the simple system. These corrections, being small compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. The complicated system can therefore be studied based on knowledge of the simpler one. In effect, it is describing a complicated unsolved system using a simple, solvable system. Approximate Hamiltonians Perturbation theory is an important tool for de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)