|
Quantile Regression
Quantile regression is a type of regression analysis used in statistics and econometrics. Whereas the method of least squares estimates the conditional ''mean'' of the response variable across values of the predictor variables, quantile regression estimates the conditional ''median'' (or other '' quantiles'') of the response variable. here is also a method for predicting the conditional geometric mean of the response variable, Tofallis (2015). "A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation", ''Journal of the Operational Research Society'', 66(8):1352-1362/ref>.] Quantile regression is an extension of linear regression used when the conditions of linear regression are not met. Advantages and applications One advantage of quantile regression relative to ordinary least squares regression is that the quantile regression estimates are more robust against outliers in the response measurements. However, the main attraction of quantile reg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets by the most restrictive definition of the term: the terrestrial planets Mercury (planet), Mercury, Venus, Earth, and Mars, and the giant planets Jupiter, Saturn, Uranus, and Neptune. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a young protostar orbited by a protoplanetary disk. Planets grow in this disk by the gradual accumulation of material driven by gravity, a process called accretion (astrophysics), accretion. The word ''planet'' comes from the Greek () . In Classical antiquity, antiquity, this word referred to the Sun, Moon, and five points of light visible to the naked eye that moved across the background of the stars—namely, Me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Absolute Deviations
Least absolute deviations (LAD), also known as least absolute errors (LAE), least absolute residuals (LAR), or least absolute values (LAV), is a statistical optimality criterion and a statistical optimization technique based on minimizing the sum of absolute deviations (also ''sum of absolute residuals'' or ''sum of absolute errors'') or the ''L''1 norm of such values. It is analogous to the least squares technique, except that it is based on ''absolute values'' instead of squared values. It attempts to find a function which closely approximates a set of data by minimizing residuals between points generated by the function and corresponding data points. The LAD estimate also arises as the maximum likelihood estimate if the errors have a Laplace distribution. It was introduced in 1757 by Roger Joseph Boscovich. Formulation Suppose that the data set consists of the points (''x''''i'', ''y''''i'') with ''i'' = 1, 2, ..., ''n''. We want to find a function ''f'' such that f(x_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability Distribution
In probability theory and statistics, the conditional probability distribution is a probability distribution that describes the probability of an outcome given the occurrence of a particular event. Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value; in some cases the conditional probabilities may be expressed as functions containing the unspecified value x of X as a parameter. When both X and Y are categorical variables, a conditional probability table is typically used to represent the conditional probability. The conditional distribution contrasts with the marginal distribution of a random variable, which is its distribution without reference to the value of the other variable. If the conditional distribution of Y given X is a continuous distribution, then its probability density function is known as the conditional density function. The prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Importance Sampling
Importance sampling is a Monte Carlo method for evaluating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest. Its introduction in statistics is generally attributed to a paper by Teun Kloek and Herman K. van Dijk in 1978, but its precursors can be found in statistical physics as early as 1949. Importance sampling is also related to umbrella sampling in computational physics. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both. Basic theory Let X\colon \Omega\to \mathbb be a random variable in some probability space (\Omega,\mathcal,\mathbb). We wish to estimate the expected value of X under \mathbb, denoted \mathbb_\mathbb /math>. If we have statistically independent random samples X_1, \ldots, X_n, generated according to \mathbb, then an empirical estimate of \mathbb_ /math> is just : \wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz Integral Rule
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form \int_^ f(x,t)\,dt, where -\infty < a(x), b(x) < \infty and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative. In the special case where the functions and |
Indicator Function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , then the indicator function of is the function \mathbf_A defined by \mathbf_\!(x) = 1 if x \in A, and \mathbf_\!(x) = 0 otherwise. Other common notations are and \chi_A. The indicator function of is the Iverson bracket of the property of belonging to ; that is, \mathbf_(x) = \left x\in A\ \right For example, the Dirichlet function is the indicator function of the rational numbers as a subset of the real numbers. Definition Given an arbitrary set , the indicator function of a subset of is the function \mathbf_A \colon X \mapsto \ defined by \operatorname\mathbf_A\!( x ) = \begin 1 & \text x \in A \\ 0 & \text x \notin A \,. \end The Iverson bracket provides the equivalent notation \left x\in A\ \right/math> or that can be used instead of \mathbf_\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
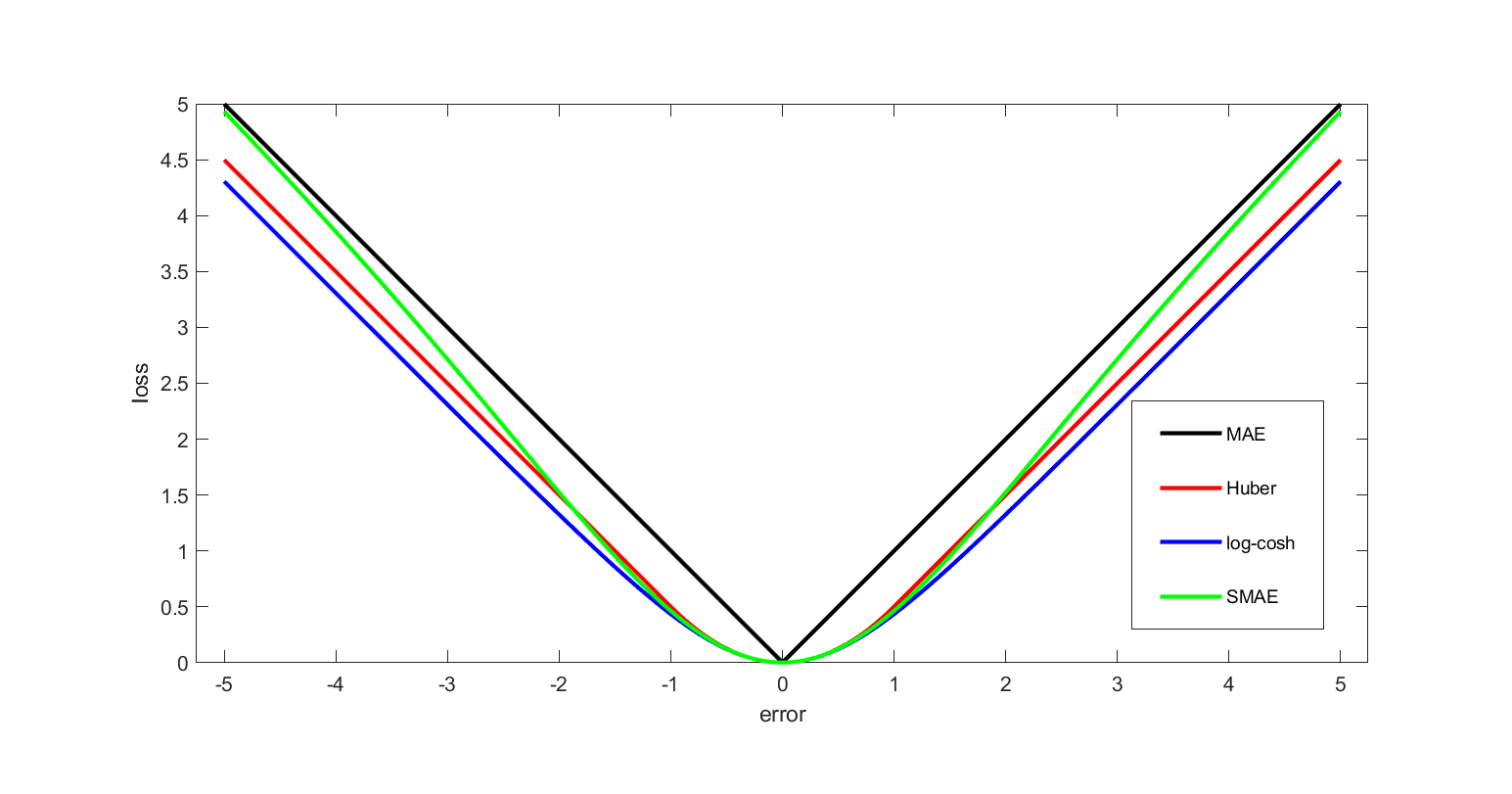
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roger Koenker
Roger William Koenker (born February 21, 1947) is an American econometrician mostly known for his contributions to quantile regression. He is currently a Honorary Professor of Economics at University College London. Education and career He finished his degree at Grinnell College in 1969 and obtained his Ph.D. in Economics from the University of Michigan in 1974. In the same year, he was employed as an assistant professor at UIUC. By 1976, he left the university to work as part of the technical staff at Bell Telephone Laboratories Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the compa .... He came back to UIUC in 1983 to teach as a William B. McKinley Professor of Economics and Statistics before becoming a Honorary Professor of Economics at UCL in 2018. Works Koenker is best known for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex Algorithm
In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming. The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are not actually used in the method, but one interpretation of it is that it operates on simplicial ''cones'', and these become proper simplices with an additional constraint. The simplicial cones in question are the corners (i.e., the neighborhoods of the vertices) of a geometric object called a polytope. The shape of this polytope is defined by the constraints applied to the objective function. History George Dantzig worked on planning methods for the US Army Air Force during World War II using a desk calculator. During 1946, his colleague challenged him to mechanize the planning process to distract him from taking another job. Dantzig formulated the problem as linear inequalities inspired by the work of Wassily Leontief, however, at tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Francis Ysidro Edgeworth
Francis Ysidro Edgeworth (8 February 1845 – 13 February 1926) was an Anglo-Irish philosopher and political economist who made significant contributions to the methods of statistics during the 1880s. From 1891 onward, he was appointed the founding editor of ''The Economic Journal''. Life Ysidro Francis Edgeworth – the order of his forenames later reversed – was born in Edgeworthstown, County Longford, Ireland, the son of Francis Beaufort Edgeworth and his wife, Rosa Florentina, daughter of exiled Catalan general Antonio Eroles. Francis Beaufort Edgeworth, when "a restless philosophy student at Cambridge on his way to Germany", had met Rosa, a teenage Spanish refugee, on the steps of the British Museum, and they subsequently eloped. Francis Beaufort Edgeworth was the son of politician, writer, and inventor Richard Lovell Edgeworth (father also of the writer Maria Edgeworth), by his fourth wife, the botanical artist and memoirist Frances Anne, daughter of the Anglica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |