|
Product
Product may refer to: Business * Product (business), an item that serves as a solution to a specific consumer problem. * Product (project management), a deliverable or set of deliverables that contribute to a business solution Mathematics * Product (mathematics) Algebra * Direct product Set theory * Cartesian product of sets Group theory * Direct product of groups * Semidirect product * Product of group subsets * Wreath product * Free product * Zappa–Szép product (or knit product), a generalization of the direct and semidirect products Ring theory * Product of rings * Ideal operations, for product of ideals Linear algebra * Scalar multiplication * Matrix multiplication * Inner product, on an inner product space * Exterior product or wedge product * Multiplication of vectors: ** Dot product ** Cross product ** Seven-dimensional cross product ** Triple product, in vector calculus * Tensor product Topology * Product topology Algebraic topology * Cap product * Cup product * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product (business)
In marketing, a product is an object, or system, or service made available for consumer use as of the consumer demand; it is anything that can be offered to a market to satisfy the desire or need of a customer. In retailing, products are often referred to as '' merchandise'', and in manufacturing, products are bought as raw materials and then sold as finished goods. A service is also regarded as a type of product. In project management, products are the formal definition of the project deliverables that make up or contribute to delivering the objectives of the project. A related concept is that of a sub-product, a secondary but useful result of a production process. Dangerous products, particularly physical ones, that cause injuries to consumers or bystanders may be subject to product liability. Product classification A product can be classified as tangible or intangible. A tangible product is an actual physical object that can be perceived by touch such as a building, ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product (mathematics)
In mathematics, a product is the result of multiplication, or an expression that identifies objects (numbers or variables) to be multiplied, called ''factors''. For example, 30 is the product of 6 and 5 (the result of multiplication), and x\cdot (2+x) is the product of x and (2+x) (indicating that the two factors should be multiplied together). The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the ''commutative law'' of multiplication. When matrices or members of various other associative algebras are multiplied, the product usually depends on the order of the factors. Matrix multiplication, for example, is non-commutative, and so is multiplication in other algebras in general as well. There are many different kinds of products in mathematics: besides being able to multiply just numbers, polynomials or matrices, one can also define products on many different algebraic structures. Product of two numbers Product of a seque ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is : A\times B = \. A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product is taken, the cells of the table contain ordered pairs of the form . One can similarly define the Cartesian product of ''n'' sets, also known as an ''n''-fold Cartesian product, which can be represented by an ''n''-dimensional array, where each element is an ''n''-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets. The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product. Examples A deck of cards An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product (category Theory)
In category theory, the product of two (or more) objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the Cartesian product of sets, the direct product of groups or rings, and the product of topological spaces. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects. Definition Product of two objects Fix a category C. Let X_1 and X_2 be objects of C. A product of X_1 and X_2 is an object X, typically denoted X_1 \times X_2, equipped with a pair of morphisms \pi_1 : X \to X_1, \pi_2 : X \to X_2 satisfying the following universal property: * For every object Y and every pair of morphisms f_1 : Y \to X_1, f_2 : Y \to X_2, there exists a unique morphism f : Y \to X_1 \times X_2 such that the following diagram commutes: *: Whether a product exists may depend on C or on X_1 and X_2. If it does exist, it is unique up to canonical isomor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
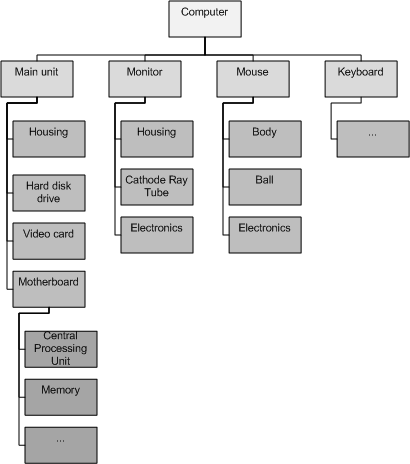
Product (project Management)
{{more citations needed, date=January 2021 In project management under the PRINCE2 methodology, a product breakdown structure (PBS) is a tool for analysing, documenting and communicating the outcomes of a project, and forms part of the product based planning technique. The PBS provides "an exhaustive, hierarchical tree structure of deliverables that make up the project, arranged in whole-part relationship" (Haughey, 2015).Duncan Haughey. (2015) ‘Project Management Tools’, Project Smart. Available from: https://www.projectsmart.co.uk/project-management-tools.php This diagrammatic representation of project outputs provides a clear and unambiguous statement of what the project is to deliver. The PBS is identical in format to the work breakdown structure (WBS), but is a separate entity and is used at a different step in the planning process. The PBS precedes the WBS and focuses on cataloguing all the desired outputs (products) needed to achieve the goal of the project. This feed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. In mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Product
In mathematics, one can often define a direct product of objects already known, giving a new one. This generalizes the Cartesian product of the underlying sets, together with a suitably defined structure on the product set. More abstractly, one talks about the product in category theory, which formalizes these notions. Examples are the product of sets, groups (described below), rings, and other algebraic structures. The product of topological spaces is another instance. There is also the direct sum – in some areas this is used interchangeably, while in others it is a different concept. Examples * If we think of \R as the set of real numbers, then the direct product \R \times \R is just the Cartesian product \. * If we think of \R as the group of real numbers under addition, then the direct product \R\times \R still has \ as its underlying set. The difference between this and the preceding example is that \R \times \R is now a group, and so we have to also say how to add their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is denoted by the symbol \times. Given two linearly independent vectors and , the cross product, (read "a cross b"), is a vector that is perpendicular to both and , and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product (projection product). If two vectors have the same direction or have the exact opposite direction from each other (that is, they are ''not'' linearly independent), or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Topology
In topology and related areas of mathematics, a product space is the Cartesian product of a family of topological spaces equipped with a natural topology called the product topology. This topology differs from another, perhaps more natural-seeming, topology called the box topology, which can also be given to a product space and which agrees with the product topology when the product is over only finitely many spaces. However, the product topology is "correct" in that it makes the product space a categorical product of its factors, whereas the box topology is too fine; in that sense the product topology is the natural topology on the Cartesian product. Definition Throughout, I will be some non-empty index set and for every index i \in I, let X_i be a topological space. Denote the Cartesian product of the sets X_i by X := \prod X_ := \prod_ X_i and for every index i \in I, denote the i-th by \begin p_i :\;&& \prod_ X_j &&\;\to\; & X_i \\ .3ex && \left(x_j\r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Of Group Subsets
In mathematics, one can define a product of group subsets in a natural way. If ''S'' and ''T'' are subsets of a group ''G'', then their product is the subset of ''G'' defined by :ST = \. The subsets ''S'' and ''T'' need not be subgroups for this product to be well defined. The associativity of this product follows from that of the group product. The product of group subsets therefore defines a natural monoid structure on the power set of ''G''. A lot more can be said in the case where ''S'' and ''T'' are subgroups. The product of two subgroups ''S'' and ''T'' of a group ''G'' is itself a subgroup of ''G'' if and only if ''ST'' = ''TS''. Product of subgroups If ''S'' and ''T'' are subgroups of ''G'', their product need not be a subgroup (for example, two distinct subgroups of order 2 in the symmetric group on 3 symbols). This product is sometimes called the ''Frobenius product''. In general, the product of two subgroups ''S'' and ''T'' is a subgroup if and only if ''ST'' = ''TS'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product
In mathematics, the tensor product V \otimes W of two vector spaces and (over the same field) is a vector space to which is associated a bilinear map V\times W \to V\otimes W that maps a pair (v,w),\ v\in V, w\in W to an element of V \otimes W denoted v \otimes w. An element of the form v \otimes w is called the tensor product of and . An element of V \otimes W is a tensor, and the tensor product of two vectors is sometimes called an ''elementary tensor'' or a ''decomposable tensor''. The elementary tensors span V \otimes W in the sense that every element of V \otimes W is a sum of elementary tensors. If bases are given for and , a basis of V \otimes W is formed by all tensor products of a basis element of and a basis element of . The tensor product of two vector spaces captures the properties of all bilinear maps in the sense that a bilinear map from V\times W into another vector space factors uniquely through a linear map V\otimes W\to Z (see Universal property). Tenso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inner Product Space
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in \langle a, b \rangle. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality (zero inner product) of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or ''scalar product'' of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898. An inner product naturally induces an associated norm, (denoted , x, and , y, in the picture); so, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |