|
Probabilistic Numerics
Probabilistic numerics is aactivefield of study at the intersection of applied mathematics, statistics, and machine learning centering on the concept of uncertainty in computation. In probabilistic numerics, tasks in numerical analysis such as finding numerical solutions for integration, linear algebra, optimization and simulation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference. Introduction A numerical method is an algorithm that ''approximates'' the solution to a mathematical problem (examples below include the solution to a linear system of equations, the value of an integral, the solution of a differential equation, the minimum of a multivariate function). In a ''probabilistic'' numerical algorithm, this process of approximation is thought of as a problem of ''estimation'', ''inference'' or ''learning'' and realised in the framework of probabilistic inference (often, but not always, Bayesian inference). Formally, this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Active Learning (machine Learning)
Active learning is a special case of machine learning in which a learning algorithm can interactively query a human user (or some other information source), to label new data points with the desired outputs. The human user must possess knowledge/expertise in the problem domain, including the ability to consult/research authoritative sources when necessary. In statistics literature, it is sometimes also called optimal experimental design. The information source is also called ''teacher'' or ''oracle''. There are situations in which unlabeled data is abundant but manual labeling is expensive. In such a scenario, learning algorithms can actively query the user/teacher for labels. This type of iterative supervised learning is called active learning. Since the learner chooses the examples, the number of examples to learn a concept can often be much lower than the number required in normal supervised learning. With this approach, there is a risk that the algorithm is overwhelmed by un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bayesian Optimization
Bayesian optimization is a sequential design strategy for global optimization of black-box functions, that does not assume any functional forms. It is usually employed to optimize expensive-to-evaluate functions. With the rise of artificial intelligence innovation in the 21st century, Bayesian optimizations have found prominent use in machine learning problems for optimizing hyperparameter values. History The term is generally attributed to and is coined in his work from a series of publications on global optimization in the 1970s and 1980s. Early mathematics foundations From 1960s to 1980s The earliest idea of Bayesian optimization sprang in 1964, from a paper by American applied mathematician Harold J. Kushner“A New Method of Locating the Maximum Point of an Arbitrary Multipeak Curve in the Presence of Noise” Although not directly proposing Bayesian optimization, in this paper, he first proposed a new method of locating the maximum point of an arbitrary multipeak curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
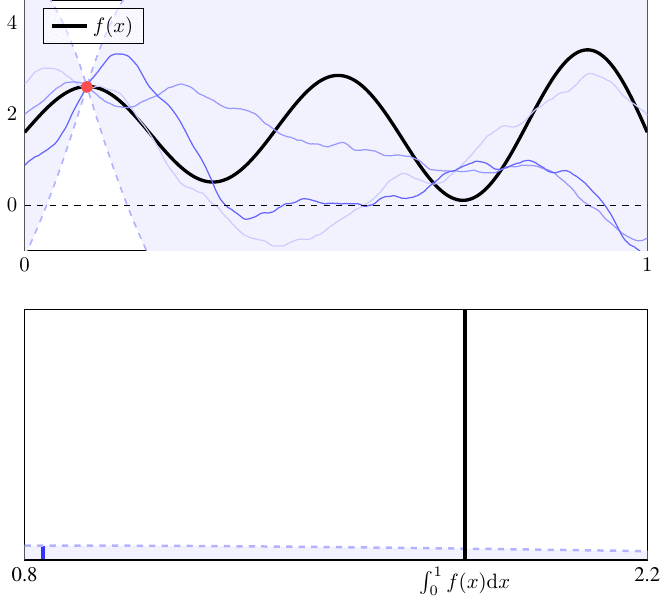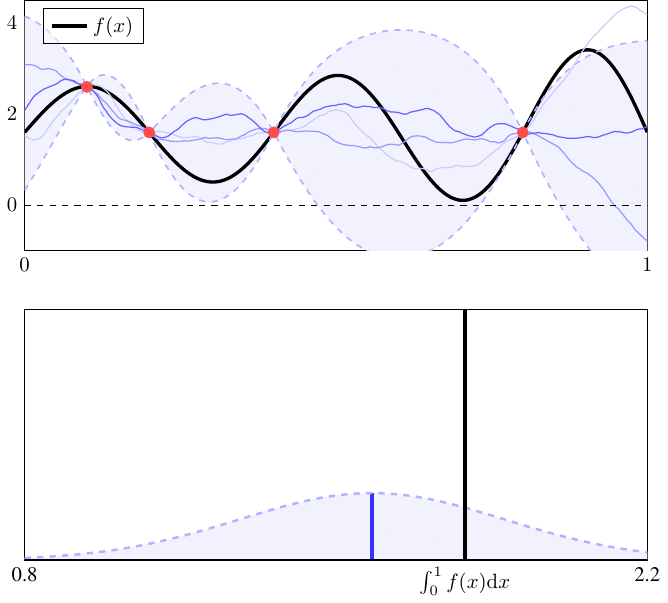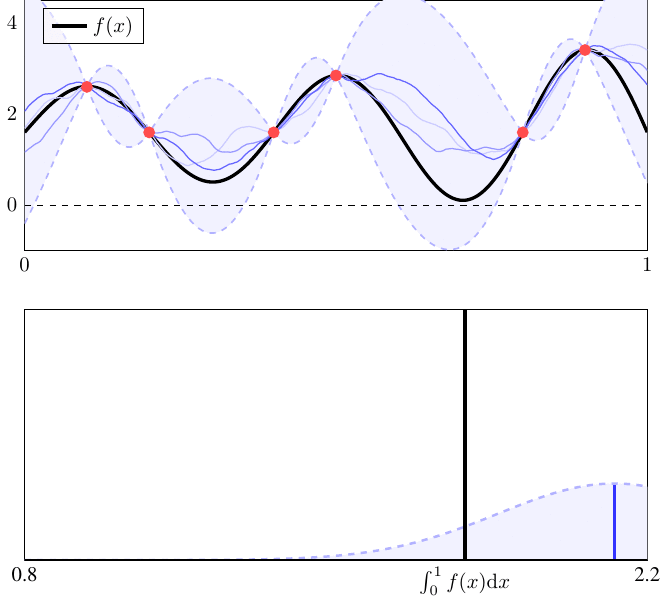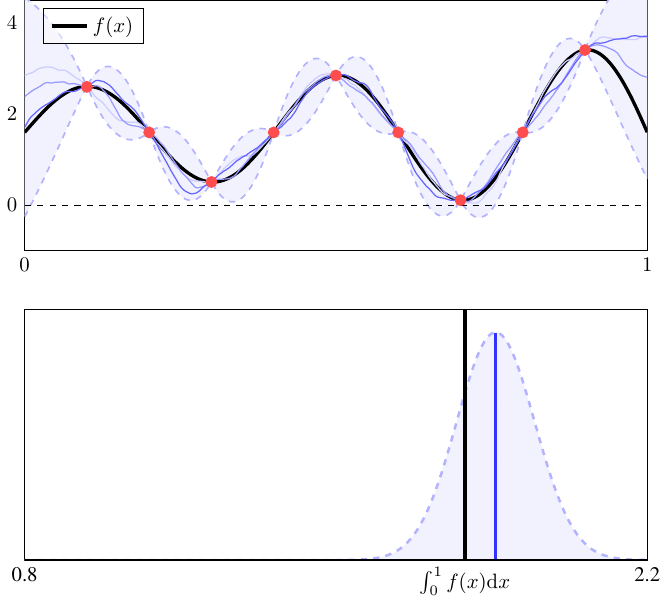
Bayesian Quadrature
Bayesian quadrature is a method for approximating intractable integration problems. It falls within the class of probabilistic numerics, probabilistic numerical methods. Bayesian quadrature views numerical integration as a Bayesian inference task, where function evaluations are used to estimate the integral of that function. For this reason, it is sometimes also referred to as "Bayesian probabilistic numerical integration" or "Bayesian numerical integration". The name "Bayesian cubature" is also sometimes used when the integrand is multi-dimensional. A potential advantage of this approach is that it provides probabilistic uncertainty quantification for the value of the integral. Bayesian quadrature Numerical integration Let f:\mathcal \rightarrow \mathbb be a function defined on a domain \mathcal (where typically \mathcal\subseteq \mathbb^d). In numerical integration, function evaluations f(x_1), \ldots, f(x_n) at distinct locations x_1, \ldots, x_n in \mathcal are used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inverse Problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects. Inverse problems are some of the most important mathematical problems in science and mathematics because they tell us about parameters that we cannot directly observe. They can be found in system identification, optics, radar, acoustics, communication theory, signal processing, medical imaging, computer vision, geophysics, oceanography, astronomy, remote sensing, natural language processing, machine learning, nondestructive testing, slope stability analys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Approximate Bayesian Computation
Approximate Bayesian computation (ABC) constitutes a class of computational methods rooted in Bayesian statistics that can be used to estimate the posterior distributions of model parameters. In all model-based statistical inference, the likelihood function is of central importance, since it expresses the probability of the observed data under a particular statistical model, and thus quantifies the support data lend to particular values of parameters and to choices among different models. For simple models, an analytical formula for the likelihood function can typically be derived. However, for more complex models, an analytical formula might be elusive or the likelihood function might be computationally very costly to evaluate. ABC methods bypass the evaluation of the likelihood function. In this way, ABC methods widen the realm of models for which statistical inference can be considered. ABC methods are mathematically well-founded, but they inevitably make assumptions and app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Best, Worst And Average Case
In computer science, best, worst, and average cases of a given algorithm express what the resource usage is ''at least'', ''at most'' and ''on average'', respectively. Usually the resource being considered is running time, i.e. time complexity, but could also be memory or some other resource. Best case is the function which performs the minimum number of steps on input data of n elements. Worst case is the function which performs the maximum number of steps on input data of size n. Average case is the function which performs an average number of steps on input data of n elements. In real-time computing, the worst-case execution time is often of particular concern since it is important to know how much time might be needed ''in the worst case'' to guarantee that the algorithm will always finish on time. Average performance and worst-case performance are the most used in algorithm analysis. Less widely found is best-case performance, but it does have uses: for example, where th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quasi-Newton Method
In numerical analysis, a quasi-Newton method is an iterative numerical method used either to find zeroes or to find local maxima and minima of functions via an iterative recurrence formula much like the one for Newton's method, except using approximations of the derivatives of the functions in place of exact derivatives. Newton's method requires the Jacobian matrix of all partial derivatives of a multivariate function when used to search for zeros or the Hessian matrix when used for finding extrema. Quasi-Newton methods, on the other hand, can be used when the Jacobian matrices or Hessian matrices are unavailable or are impractical to compute at every iteration. Some iterative methods that reduce to Newton's method, such as sequential quadratic programming, may also be considered quasi-Newton methods. Search for zeros: root finding Newton's method to find zeroes of a function g of multiple variables is given by x_ = x_n - _g(x_n) g(x_n), where _g(x_n) is the left inverse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |