|
Polygon-circle Graph
In the mathematics, mathematical discipline of graph theory, a polygon-circle graph is an intersection graph of a set of convex polygons all of whose vertex (geometry), vertices lie on a common circle. These graphs have also been called spider graphs. This class of graphs was first suggested by Michael Fellows in 1988, motivated by the fact that it is closed under edge contraction and induced subgraph operations.. A polygon-circle graph can be represented as an "alternating sequence". Such a sequence can be gained by perturbing the polygons representing the graph (if necessary) so that no two share a vertex, and then listing for each vertex (in circular order, starting at an arbitrary point) the polygon attached to that vertex. Closure under induced minors Edge contraction, Contracting an edge of a polygon-circle graph results in another polygon-circle graph. A geometric representation of the new graph may be formed by replacing the polygons corresponding to the two endpoints ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convex Hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a Bounded set, bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its projective duality, dual problem of intersecting Half-space (geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Mathematics (journal)
''Discrete Mathematics'' is a biweekly peer-reviewed scientific journal in the broad area of discrete mathematics, combinatorics, graph theory, and their applications. It was established in 1971 and is published by North-Holland Publishing Company. It publishes both short notes, full length contributions, as well as survey articles. In addition, the journal publishes a number of special issues each year dedicated to a particular topic. Although originally it published articles in French and German, it now allows only English language articles. The editor-in-chief is Douglas West ( University of Illinois, Urbana). History The journal was established in 1971. The first article it published was written by Paul Erdős, who went on to publish a total of 84 papers in the journal. Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact facto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Clique Number
In graph theory, a clique ( or ) is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph G is an induced subgraph of G that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph (the clique problem) is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied. Although the study of complete subgraphs goes back at least to the graph-theoretic reformulation of Ramsey theory by , the term ''clique'' comes from , who used complete subgraphs in social networks to model cliques of people; that is, groups of people all of whom know each other. Cliques have many other applications in the sciences and particularly in bioinformatics. Definitions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chromatic Number
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an '' edge coloring'' assigns a color to each edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Perfect Graph
In graph theory, a perfect graph is a Graph (discrete mathematics), graph in which the Graph coloring, chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices. The perfect graphs include many important families of graphs and serve to unify results relating Graph coloring, colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time, despite their greater complexity for non-perfect graphs. In addition, several important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem (gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circular Arc Graph
In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect. Formally, let :I_1, I_2, \ldots, I_n \subset C_1 be a set of arcs. Then the corresponding circular-arc graph is ''G'' = (''V'', ''E'') where : V = \ and : \ \in E \iff I_\alpha \cap I_\beta \neq \varnothing. A family of arcs that corresponds to G is called an ''arc model''. Recognition demonstrated the first polynomial recognition algorithm for circular-arc graphs, which runs in (n^3) time. gave the first linear ((n+m)) time recognition algorithm, where m is the number of edges. More recently, Kaplan and Nussbaum developed a simpler linear time recognition algorithm. Relation to other graph classes Circular-arc graphs are a natural generalization of interval graphs. If a circular-arc graph ''G'' has an arc model that leaves some point of the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
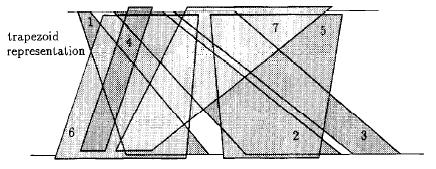
Trapezoid Graph
In graph theory, trapezoid graphs are intersection graphs of trapezoids between two horizontal lines. They are a class of co-comparability graphs that contain interval graphs and permutation graphs as subclasses. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding trapezoids intersect. Trapezoid graphs were introduced by Dagan, Golumbic, and Pinter in 1988. There exists (n\log n) algorithms for chromatic number, weighted independent set, clique cover, and maximum weighted clique. Definitions and characterizations Given a channel, a pair of two horizontal lines, a trapezoid between these lines is defined by two points on the top and two points on the bottom line. A graph is a trapezoid graph if there exists a set of trapezoids corresponding to the vertices of the graph such that two vertices are joined by an edge if and only if the corresponding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circle Graph
In graph theory, a circle graph is the intersection graph of a Chord diagram (mathematics), chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of Chord (geometry), chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other. Algorithmic complexity After earlier polynomial time algorithms, presented an algorithm for recognizing circle graphs in near-linear time. Their method is slower than linear by a factor of the inverse Ackermann function, and is based on lexicographic breadth-first search. The running time comes from a method for maintaining the split decomposition of a graph incrementally, as vertices are added, used as a subroutine in the algorithm. A number of other problems that are NP-complete on general graphs have polynomial time algorithms when restricted to circle graphs. For instance, showed that the treewidth of a circle graph can be determined, and an optim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''. Somewhat more precisely, a problem is NP-complete when: # It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no". # When the answer is "yes", this can be demonstrated through the existence of a short (polynomial length) ''solution''. # The correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. Hence, if we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Edge Contraction
In graph theory, an edge contraction is an operation that removes an edge from a graph while simultaneously merging the two vertices that it previously joined. Edge contraction is a fundamental operation in the theory of graph minors. Vertex identification is a less restrictive form of this operation. Definition The edge contraction operation occurs relative to a particular edge, e. The edge e is removed and its two incident vertices, u and v, are merged into a new vertex w, where the edges incident to w each correspond to an edge incident to either u or v. More generally, the operation may be performed on a set of edges by contracting each edge (in any order). The resulting graph is sometimes written as G/e. (Contrast this with G \setminus e, which means simply removing the edge e without merging its incident vertices.) As defined below, an edge contraction operation may result in a graph with multiple edges even if the original graph was a simple graph. However, some a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |